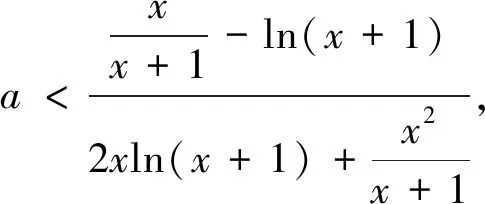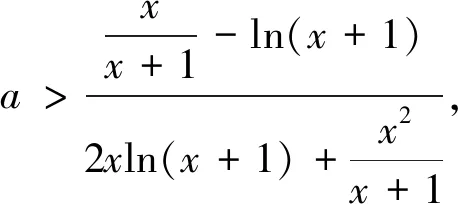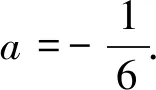2018全国Ⅲ(21)题的命题背景及解法探究
2019-04-28安徽省合肥市一六八中学230601
中学数学研究(江西) 2019年4期
安徽省合肥市一六八中学 (230601)
谈世勇
例(2018全国3卷第21题)已知函数f(x)=(2+x+ax2)ln(x+1)-2x.
(1)若a=0,证明:当-1
(2)若x=0是f(x)的极大值点,求a.
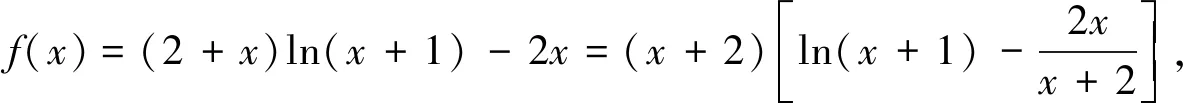
(2)尝试一:(极大值点的第二充要条件:已知函数y=f(x)在x=x0处各阶导数都存在且连续,x=x0是函数的极大值点的一个充要条件为前2n-1阶导数等于0,第2n阶导数小于0.)
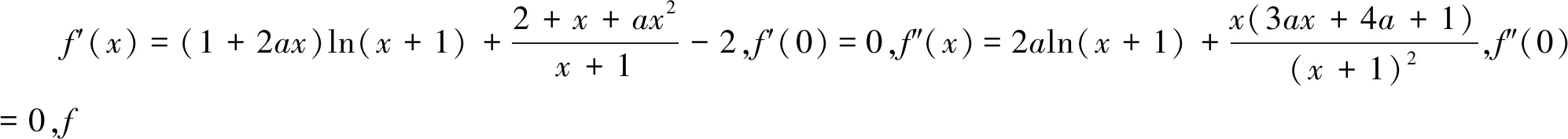


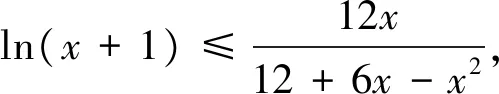
证明:h′(x)=q′(x)f(x)+q(x)f′(x)-

f′(x0)=g′(x0),且f(x0)=g(x0),代入化简即得h′(x0)=0.
引理2 已知函数y=f(x)在x=x0处各阶导数都存在且连续,x=x0是函数的极大值点的一个充要条件为前2n-1阶导数等于0,第2n阶导数小于0.
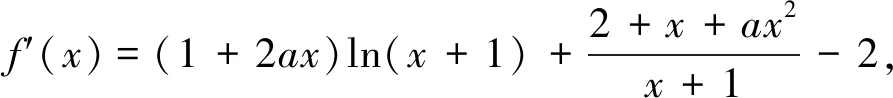
尝试二:若x=0是f(x)的极大值点,注意到f′(0)=0,则存在充分接近于0的δ,使得当x∈(-δ,0)时,f′(x)>0,当x∈(0,δ)时,f′(x)<0(*),得到一个恒成立问题,其基本方法之一有分离参数法.