毫米波大规模阵列天线波束扫描研究*
2019-05-31金红军赵怀松
王 舟 ,金红军 ,赵怀松
(1.杭州电子科技大学 电子信息学院,浙江 杭州 310018;2.中国电子科技集团公司第五十研究所,上海 200331)
0 引 言
随着互联网移动通讯技术的快速发展,高速数据传输业务以及无处不在的通讯需求正呈现出井喷式的增长。用户对既快速又安全可靠的无线通讯需求不断增长,而目前的4G网络通讯技术只能带来近似100 Mb/s的传输速率,百兆级的通讯服务已不能满足未来移动通讯的发展需求。现阶段,低频段无线电技术的频谱资源在开发中已经利用殆尽,换句话说,即使低频段中的调制分集复用技术再先进,也很难使传输速率和传输质量有实质性的提高,也不能满足目前急剧增长的无线通讯需求[1]。
根据预测,未来几年内对无线网络通讯业务的需求量将是目前的上千倍,而且,在即将到来的5G时代,微基站将代替现有的庞大基站,其定会分布的更密集,对网络吞吐量、传输质量和安全性的要求也将更苛刻。因此,急需提高无线接入网的容量、提高通讯链路的传输速度、开发利用高频段的频谱资源、拓宽瞬时射频频带。目前使用的第四代蜂窝网络多天线技术,越来越难以负荷急速增长的业务数据流量。而5G通信网络已经开展了毫米波大规模阵列天线技术的研究,结合波束赋形技术不仅能够获得高增益高速率,还克服了毫米波路径损耗严重的问题,所以本文对毫米波大规模阵列天线中波束扫描技术进行研究。
1 波束码本
对于精确的相移和幅度调整的波束赋形技术需要大量的数据进行训练,而且开销也比较大,这有违毫米波系统对于低功率低复杂度的要求。为了降低系统的复杂度,DFT码本仅生成相移,没有进行任何幅度调整。同IEEE802.15.3c中的码本以及N相位码本相比[2-3],DFT码本设计更加灵活且在任意波束方向上没有任何增益损失,文献[4]给出了其波束向量矩阵的数学表达式:

其中m=1∶M;n=1∶N,图1给出了不同阵元数的波束图。


图1 基于DFT码本的波束图
2 波束扫描
2.1 二分扫描
二分扫描算法的思想来源于二分查找算法,其主要思想为:在360度的空间范围内,首先利用较宽的扇区来覆盖,然后扫描获取最优扇区对,再将最优扇区对二分成宽度较细的两个波束,然后再扫描获取最优波束,不断重复上述操作。在每一次波束细化的过程中,阵元数会跟着加倍,当产生波束的阵元数等于实际阵元数时,二分扫描结束,最终获取的波束对即为最优波束对。
假设收发端的阵元数目为N,为方便分析,假设阵元数目为2p。波束数目为阵元数目的2倍,即2p+1。在扫描的过程中,只要在2个扇区之间扫描即可,扫描次数为4次。对于阵元数目为2p的阵列,需要p次的迭代,除首次需要16次的扫描以外,其余仅需要4次,则总共的扫描次数为4(p+4)=4(log2N+4)次,其扫描复杂度为o(log2N)。图2给出了阵元数目为16,波束数目为32时二分扫描算法逐步细化波束过程。
2.2 波束旋转
波束旋转[5]即在原先波束权值的基础乘以旋转向量,使得单个波束在一定范围转动,即两个波束之间。以下为波束旋转生成3个波束的公式:

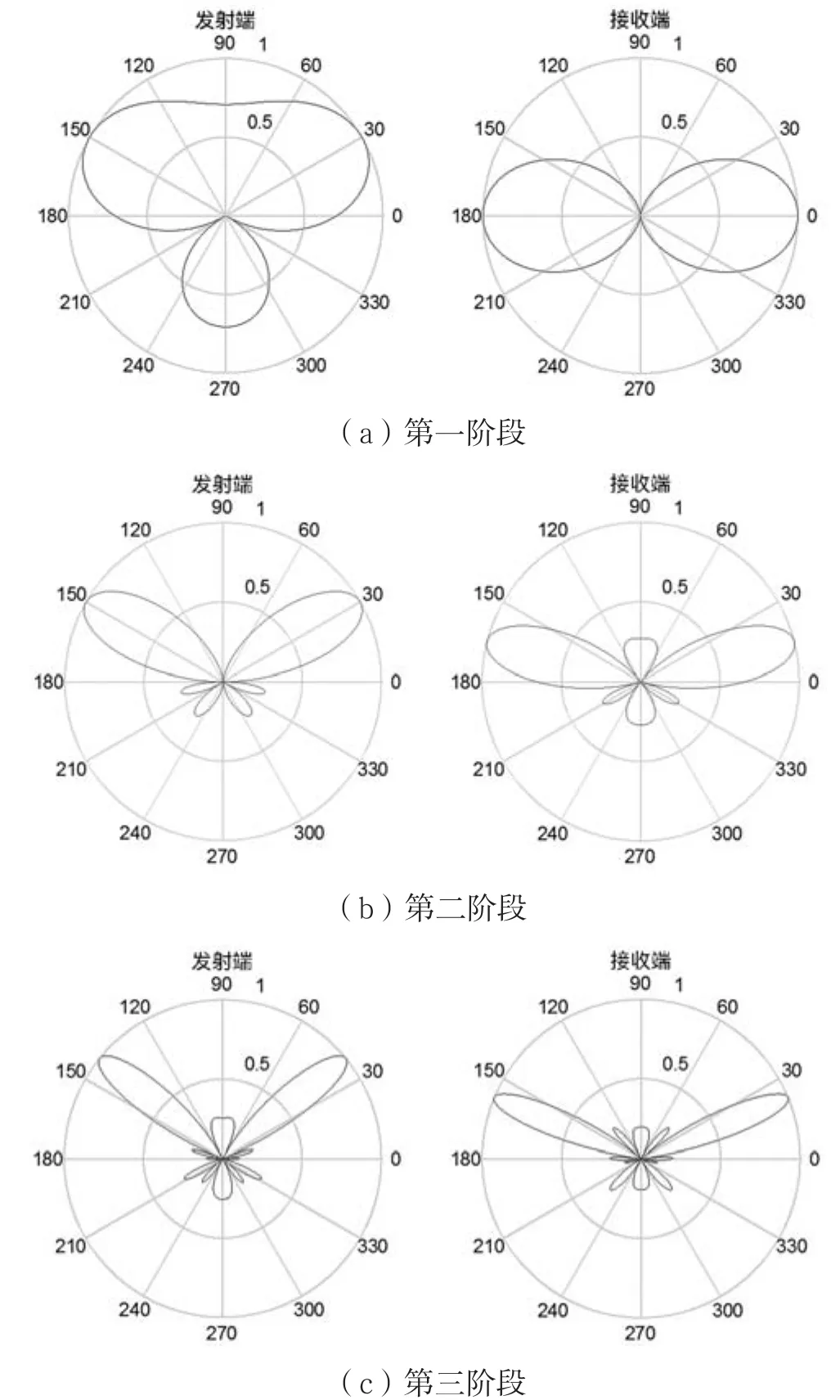
图2 二分扫描过程图
bm为原来的波束,m=1:M,rk=0:2,以下为波束旋转生成5个波束的公式:
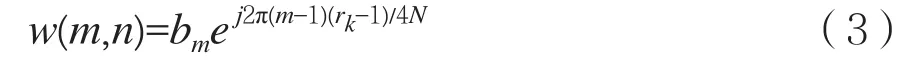
bm为原来的波束,m=1:M,rk=-1:3,图3给出了波束旋转生成3个和5个波束的波束图。由图3可知,波束经过小角度的旋转之后可以很好的覆盖原有波束交界处无波束覆盖的问题,从而有效避免在波束交界处增益低的问题。波束旋转生成5个波束的方式相比于生成3个波束会更加密集,所以为使后续的波束扫描仿真具有更明显的效果,我们会采用波束旋转后产生5个波束的方式。
3 仿真分析
3.1 波束旋转有效性仿真
为方便实验对比,仿真实验在发射端使用32阵元的天线阵列,波束数目为64,而在接收端产生波束使其指向发射端某两个波束中间,在接收端通过比较波束旋转前后获得的最大信噪比,来验证波束旋转的有效性,图4给出了100次的仿真实验结果。

图3 波束旋转
由图4波束旋转前后的比较可知,波束旋转之后的整体增益明显高于波束旋转之前,波束旋转之后的增益值基本稳定在35 dB至58 dB之间,而波束旋转之前的增益却2 dB至50 dB之间变化,尤其在第75次实验中,波束旋转之后将波束旋转前的2 dB拉升到了42 dB,提升了近40 dB,由此可以证明,利用波束旋转可以有效避免波束交界处增益低的问题,使得波束扫描后的最优波束具有更大增益。
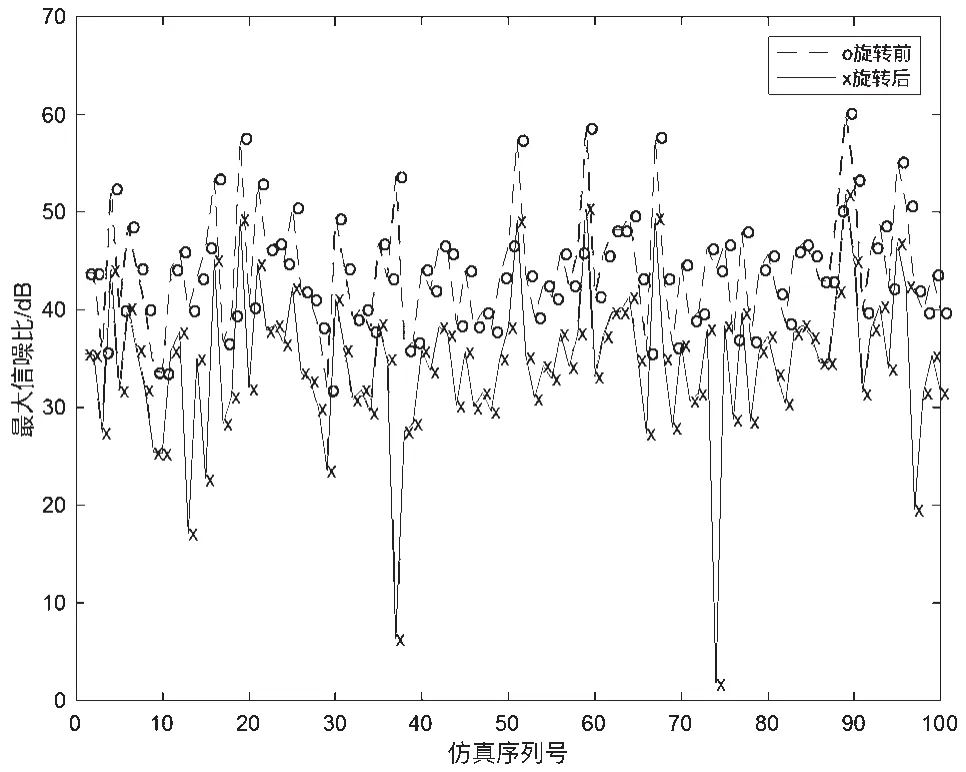
图4 波束旋转前后比较
3.2 基于穷举扫描算法的波束旋转仿真
在穷举扫描算法最终获得最优波束对之后,利用波束旋转的方式可以来弥补波束交界处低增益的问题,如果穷举扫描的结果中出现几组信噪比相同的最优波束对,那么我们将每一组波束对进行波束旋转之后,再选取其中信噪比最大的作为最优波束对,由此可知,经过波束旋转前后获得最优波束对可能为同一波束对,也有可能不是同一波束对,即当接收端波束方向接近发射端两波束交界处时。下图5给出了阵元数目为32,波束数目为64时,应用波束旋转前后的100次实验增益结果。
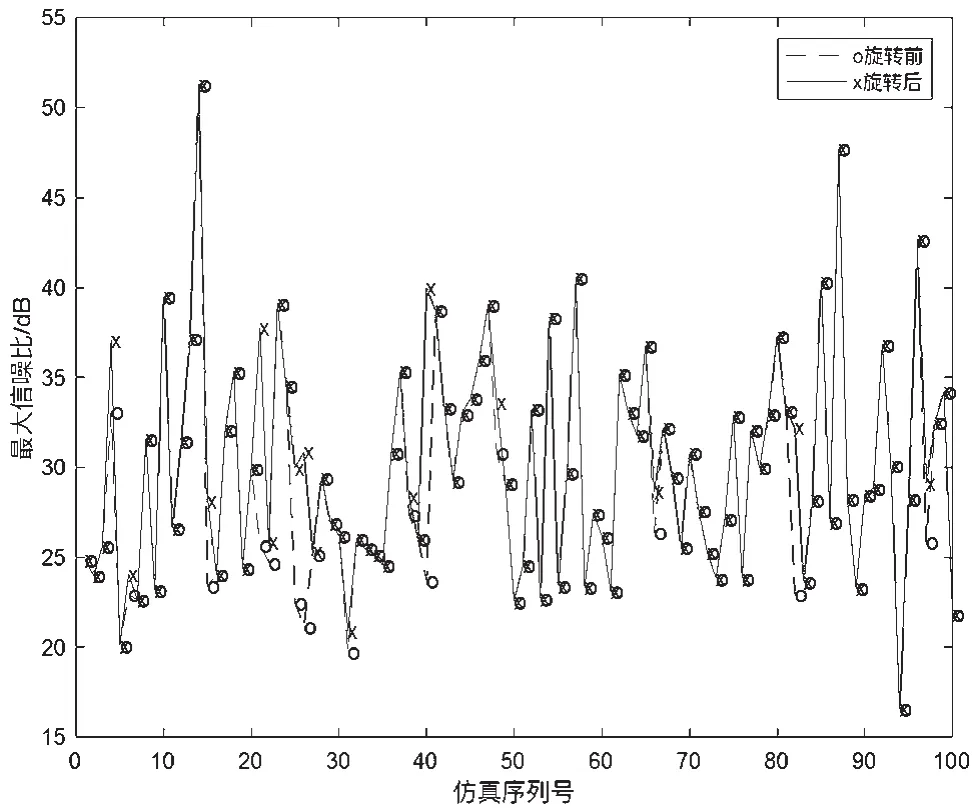
图5 基于穷举扫描算法的波束旋转
3.3 基于二分扫描算法的波束旋转仿真
波束旋转将应用在二分扫描每一阶段获取最优扇区对之后,经过波束旋转获取新的最优扇区对,再继续执行下一阶段的扫描。在波束扫描的每一阶段使用波束旋转而不是最后一个阶段,可以使获得的增益最大化。图6给出了阵元数目为32,波束数目为64时,波束旋转前后二分扫描算法结果的100次仿真实验。
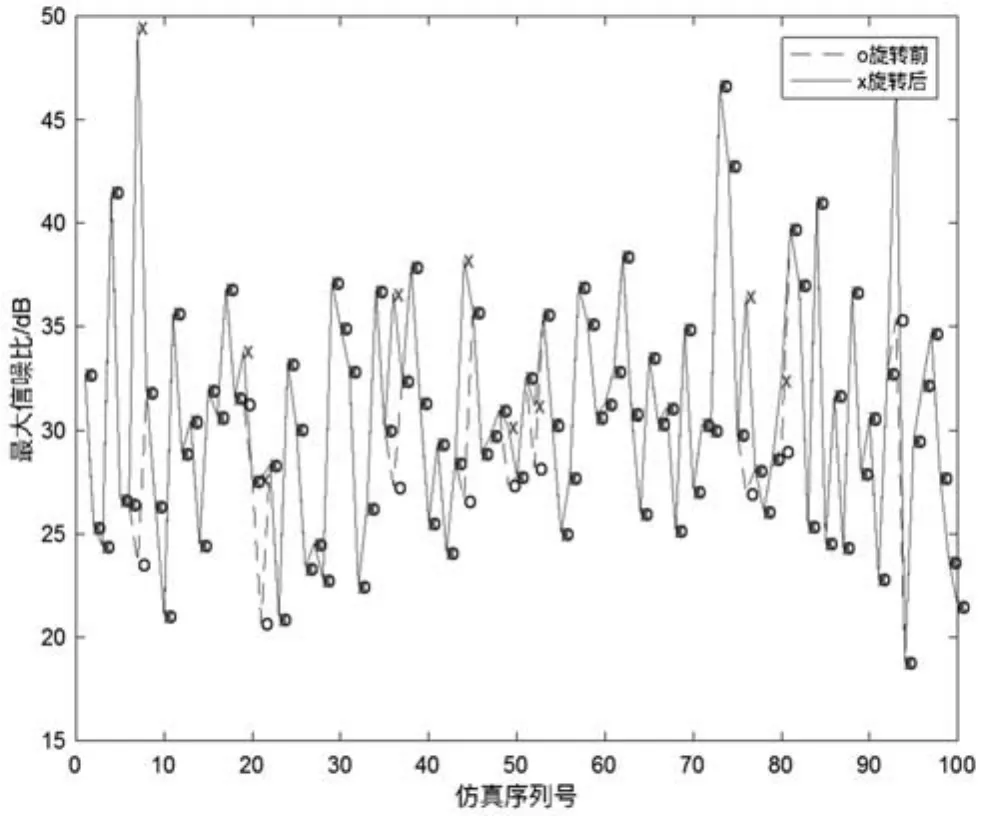
图6 基于二分扫描算法的波束旋转
由图6可以看出,实验结果得到了与在穷举扫描算法中类似的效果,但总体优化次数较穷举扫描算法更多,其中也发现了波束旋转前后增益差距较大的情况,如仿真中的第8次实验,从23 dB提升到了49 dB,此情况可能是二分扫描每个阶段增益叠加的结果,因为穷举扫描中,波束旋转只在获得最优波束对之后旋转,只能在一次波束旋转之后选择其中最优波束对,而在二分扫描过程中,每一阶段都实现波束旋转,可能就会出现每一阶段在波束旋转之后都获得了更优的波束对,所以会出现如第10次实验中增益差距较大的情况。由此也说明了波束旋转有效优化了扫描效率更高的二分扫描算法。
4 结 语
本文针对毫米波大规模阵列天线中波束交界处增益低的问题,在基于DFT波束码本,穷举扫描算法以及二分扫描算法,提出利用波束旋转技术,最高使穷举扫描增益提升17 dB,二分扫描增益提升26 dB,仿真结果有效解决波束交界处增益低的问题。
