含关节间隙的3-CPaRR并联机构的运动学和动力学分析

朱景原， 王 见， 丁泽华， 周 辉， 曹 毅,3,4

(1. 江南大学 机械工程学院，江苏 无锡 214122;2. 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122;3. 机器人技术与系统国家重点实验室，哈尔滨 150080; 4. 系统控制与信息处理教育部重点实验室，上海 200240)

在传统的多体机械系统分析中，为简化其运动学和动力学模型，运动关节被假定为理想关节[1-3]。然而，实际杆件因制造误差，关节元素装配误差和磨损效应，以及构件变形和材料缺陷等因素，关节连接处的间隙不可避免[4-7]。关节间隙使得理想的低副关节有可能成为高副关节，引起关节间的冲击现象，进而对关节元素瞬时施加和移除冲击所产生的接触力。这种冲击所产生的接触力容易导致机械系统的非线性响应，从而引起整个机构的振动与噪声，降低系统的可靠性、稳定性、精度和机械部件的使用寿命[8-9]。关节间隙同时也会引起冲击动载荷，影响系统载荷的传递，造成数值预测和实验测量之间的重要偏差[10]。

近几年，随着机构性能向高精度，高速度和轻量化的方向发展，对系统动力学响应预测的要求越来越高，因此含间隙机构的动力学研究已成为机械工程领域所要解决的关键问题之一。Flores等[11-12]综合数值计算和试验模拟的方法对含间隙旋转关节的曲柄滑块机构进行了动态响应的研究。Xu等[13-15]对含间隙平面2-DOF拾取器的动态性能进行了分析。Pereira等[16]分析了实际圆柱副接触力模型的适用范围，并评估不同接触模型对多体系统动态响应的影响。Muvengei等[17-18]对具有不同位置的无摩擦旋转关节的平面多体系统参数进行了数值分析。为消除间隙引起关节元素间的冲击，Varedi等[19]优化了机构连杆的质量分布。Bai等[20]提出了定量分析方法研究具有含间隙旋转铰关节的多体机械系统的动力学特性。Zhao等[21-22]研究了平面机构的关节间隙和润滑作用对系统动态性能和关节磨损的影响。Erkaya等[23-25]对比研究了间隙对传统关节和含柔顺结构关节的影响。上述文献表明，目前对含关节间隙的机械系统运动学和动力学特性的研究主要集中在平面机构系统中，而对含间隙空间多体系统运动学和动力学的研究相对较少[26]。

接触和碰撞是多体机械系统运动的典型现象，含间隙的关节模型是建立含间隙多体系统动力学模型的重要内容之一，合理的建立关节间隙模型对含间隙机构的设计和分析至关重要。目前机构中关节间隙模型的研究方法有：扰动坐标法[27-28]、模糊法[29]、间隔分析法[30]、基于小位移螺旋理论等。

基于上述背景，本文以3-CPaRR并联机构为研究对象。基于该并联机构的运动学约束，首先研究了该并联机构的运动学规律；基于运动学分析，利用正态分布概率统计模型建立了含间隙转动关节径向和轴向的运动学模型，进而建立了含关节间隙支链运动学模型；然后，建立了间隙关节元素间法向和切向的接触力模型，并基于非完整Lagrange方程法建立了含间隙并联机构的动力学模型；另外，通过实例计算详细分析了关节间隙对并联机构运动学特性和动态响应的影响；最后通过与标准正态分布模型对比，分析定义关节元素初始接触时的间隙量为μ值的物理意义。

1 含关节间隙并联机构的运动学分析

1.1 3-CPaRR并联的结构描述及其运动学分析

3-CPaRR并联机构由动平台、定平台机架及三条结构完全对称的支链组成，每条支链由构件AiBi,BiCi,CiDi和DiEi(i=1, 2, 3 )组成，其中构件BiCi为平行四边形铰链结构，支链各构件之间以及支链与动平台之间皆通过销轴连接，如图1所示。

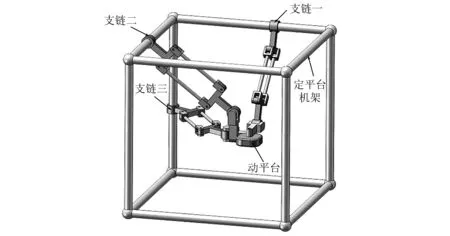
图1 3-CPaRR并联机构模型简图Fig.1 Schematic diagram of the 3-CPaRR parallel mechanism

为研究该并联机构的运动学特性，首先建立该并联机构的参考坐标系，如图2所示。其中定坐标系O-XYZ设在定平台支架上。动坐标系op-xyz初始姿态与定坐标系设定一致，原点op位于动平台几何形心处。记构件AiBi,BiCi,CiDi和DiEi的长度分别为l1i,l2i,l3i和l4i(i=1, 2, 3 )，动平台的长为lx，宽为ly，高为lz(同动坐标系x,y,z轴方向定义)。三条支链中，圆柱副A1,A2与平面XOY所成角度分别为θ1,θ2，平行四边形铰链转动副B1,B2与平面XOY所成角度分别为θ4,θ5，圆柱副A3轴线、平行四边形铰链转动副B3与平面YOZ所成角度分别为θ3,θ6。

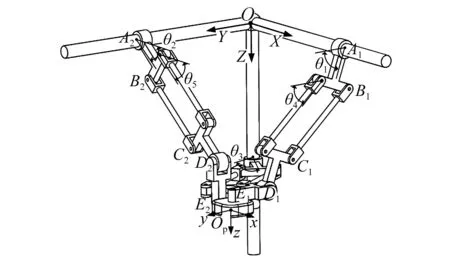
图2 3-CPaRR并联机构坐标系Fig.2 The coordinate systems of the 3-CPaRR parallel mechanism

基于该3-CPaRR并联机构结构特征及坐标系设定，三条支链与动平台连接点(即转动副E1,E2,E3的中心点)在定坐标系O-XYZ下的位置矢量Ei(i=1, 2, 3)可由其在动坐标系op-xyz下的位置矢量ei(i=1, 2, 3)表示

(1)

取Z-Y-X型欧拉角(α,β,γ)表示动坐标系op-xyz到定坐标系O-XYZ的齐次转换矩阵，则

(2)

式中：s, c为sin, cos函数的简化表示；(Xp,Yp,Zp)T为动坐标系原点op在定坐标系O-XYZ中的位置坐标。

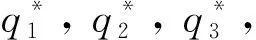
(3)

联立式(1)～式(3)可得

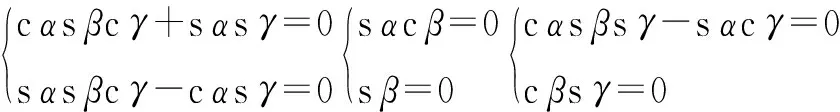
(4)

由式(4)进而求解可得：α=0，β=0，γ=0。

基于上述分析，可以得出：① 3-CPaRR并联机构具有三个移动自由度，且在空间正交方向上的移动输入与输出完全解耦；② 转动副Ei(i=1, 2, 3 )为消极转动副，在机构运动时，皆不发生转动，故该并联机构可以简化为3-CPaR机构。

基于该并联机构的运动学特征，由闭链约束可得各支链的封闭方程，如式(5)所示，由封闭方程可得各转动关节的广义坐标θi(i=1, 2, …,6 )与机构尺寸参数之间约束关系

(5)

1.4 含间隙的关节结构描述

3-CPaRR并联机构中各转动关节皆为被动转动关节，故驱动圆柱副Ai(i=1, 2, 3 )可以等效为驱动移动副和被动转动副，如图3所示。因此，本文同时对三个等效驱动圆柱副Ai中的被动转动副添加关节间隙来进行分析，其具体原因如下：① 同时考虑三个支链含关节间隙，可以更好体现间隙对该并联机构动态性能的影响；② 因该并联机构具有输入与输出完全解耦特性，且无过约束机构，根据误差逐级放大影响特性选择驱动关节含关节间隙较其他被动关节含关节间隙，更能体现关节间隙对系统动力学特性的影响[31]；③ 等效圆柱副中的驱动移动副间隙量较被动转动副关节间隙量小，所以不考虑其间隙对并联机构的影响。另外，为便于后文对该并联机构标注和计算，可等效移动副和转动副的圆柱副仍以圆柱副Ai所在的空间位置标注，且动力学计算过程中，不考虑因转动关节与移动关节轴线不重合引起的误差。

图3 圆柱副结构等效示意图Fig.3 Equivalent schematic diagram of cylindrical pair

2 含关节间隙并联机构的运动学模型

由引言所述，并联机构中的关节间隙必然存在，且在机构运动过程中，关节间隙必然引起关节元素间的相对位置发生变化，且这种变化具有一定随机性的。为分析随机变化的关节间隙对整个机构动态特性的影响，本文利用正态分布概率统计模型建立转动关节径向和轴向的运动学模型，研究关节间隙在机构运动过程中的变化规律，并进一步分析关节间隙对机构动态特性的影响。

2.1 含间隙的关节运动学模型

基于右手定则建立关节坐标系Or-XrYrZr，其中Xr轴和Yr轴指向k杆和k+1杆的长度方向。图4中:r,R为轴与轴套半径;Oa，Or分别为轴与轴套端面的中心点；er，ea分别为轴与轴套径向和轴向的间隙矢量，其对应的单位矢量为nr=er/er，na=ea/ea;ζ∈(0, 2π)为间隙矢量er相对于关节坐标系Xr轴正方向的夹角，如图4所示。

图4 含关节间隙的转动关节模型Fig.4 The model of revolute joint with clearance

为反映径向间隙矢量随机构运动变化的随机性和不确定性，由概率论与数理统计原理，定义径向间隙矢量值的随机分布服从正态分布，可得径向间隙的分布概率密度函数，其表达形式为

(6)

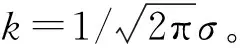
由式(6)可知，任一时刻轴与轴套的中心轴之间偏心距er为

(7)

(8)

式中：δr为轴与轴套碰撞时穿击深度值;cr为轴与轴套初始接触时的径向间隙值。

基于转动副的几何结构特征，考虑轴与轴套间的径向间隙与轴向间隙，文献[32]给出了关节元素间13种接触模式与存在条件。3-CPaRR并联机构转动副轴向长度相对较短，轴与轴套间的接触多以线、面接触为主，因而不考虑轴与轴套间点接触的倾斜情形。同上述分析方法，随机构运动，关节间隙矢量值在轴向随机变化，对于轴向间隙矢量ea，其概率密度函数的形式构造为

(9)

式中：zr为关节间隙坐标;ea max为轴套与轴轴向方向的最大间隙。

式(9)表示轴向间隙矢量出现在关节坐标系中某一轴向坐标位置的概率，由式(9)可知轴与轴套端面之间的距离ea为

(10)

(11)

式中：δa为轴与轴套碰撞时穿击深度值；ca为轴与轴套开始接触时的轴向间隙值。

2.2 含关节间隙的支链运动学模型

杆k、杆k+1为由转动销轴连接的两杆，销轴与杆k+1固接，杆k+1相对于杆k可沿转动副做径向、轴向方向的相对移动。经分析，转动副销轴的径向移动量被限制在半径为er的圆形区域内(即宽度为2×er的圆环区域)，由间隙矢量计算，杆k+1上任意一点Q相对于k杆的位置可以确定，如图5所示。

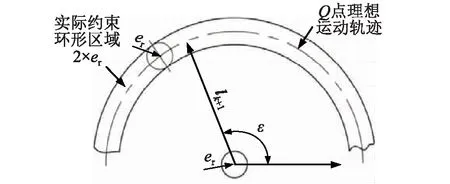
图5 含间隙转动关节运动学模型Fig.5 Kinematic model for the revolute joint with clearance

图5中：lk+1为杆k+1上的Q点到转动轴中心的径向矢量；ε为杆件k+1在系统坐标系下的相对转动角度。

则Q点在关节坐标系中径向坐标可以得到

(12)

定义因间隙引起的杆件在关节坐标系下长度变化量为虚长度Δlk+1，则

(13)

同理，由关节轴向间隙引起的Q点轴向的坐标为

zQ=zr+ea

(14)

综合式(12)、式(14)，可推出考虑关节间隙时杆k+1件上Q点在关节坐标系中的坐标(xQyQzQ)T。

3 含间隙转动关节的接触力模型

理想转动关节仅含有一个转动自由度，因关节间隙的存在，如不考虑销轴在轴套内的倾斜情况，则关节元素为4自由度的转动关节。由于关节间隙量较小，可忽略轴在轴套中产生的惯性力，如仅考虑与轴套发生接触碰撞时产生的碰撞力与摩擦力，则含间隙转动关节的碰撞接触运动模型，如图6所示。

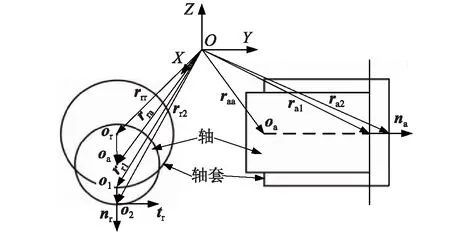
图6 含间隙转动关节的接触运动模型Fig.6 Kinematic model for contactof the revolute joint with clearance

图6中，O1，O2为关节元素轴与轴套在系统坐标系下的接触碰撞点，其在系统坐标系下的矢量rr1,rr2分别为

(15)

式(15)对时间求导，可得径向接触速度的法向速度矢量vnr和切向速度矢量vtr

(16)

因不考虑销轴在轴套内的倾斜情况，故不考虑轴与轴套在轴端面的切向相对接触速度和切向接触力，则轴向接触速度的法向速度矢量vna为

(17)

含间隙机构接触碰撞模型主要集中在离散分析法和连续接触分析方法，其中连续接触力模型被广泛应用于含有间隙的机构的接触冲击分析中。目前，连续接触力模型应中以Lankarani-Nikravesh接触力模型和Flores接触力模型应用较为广泛，相比Lankarani-Nikravesh接触力模型Flores接触力模型不受限于恢复系数大小选择的限制，更适用于一般机械结构之间的碰撞，另外，该模型不仅结构相对简单且拥有稳定的数值解，因此本文采用Flores接触力模型。

(18)

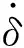
(19)

式中：vi与vj分别为接触体i,j的泊松比;Ei与Ej分别为接触体i,j的弹性模量;Ri与Rj分别为接触体i,j的接触半径。

为描述偏心碰撞中接触元素之间出现的切向摩擦力，本文采用Ambrósio[34]提出的修正Coulomb摩擦模型。

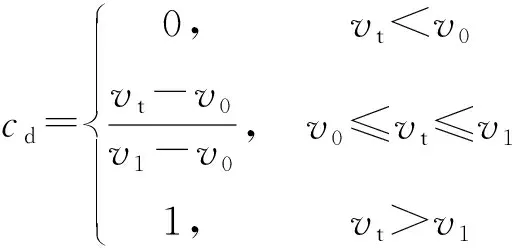
(20)

式中：ud为滑动摩擦因数;cd为动态修正系数；vt为切向速度;v0，v1为给定的速度界限。

4 含关节间隙3-CPaRR并联机构的动力学模型

4.1 含关节间隙并联机构中的广义力的转化

含关节间隙的3-CPaRR并联机构的等效圆柱副Ai本质为不含间隙的移动副和含间隙的转动副，由于轴向的法向接触力位于转动关节轴套与销轴端面的接触点处，因此要将接触点处的接触力向构件的质心转化，综上所述，含间隙等效圆柱副Ai的接触力为Fif。

Fif=Finn+Fitt+Fian(i=1, 2, 3 )

(21)

为建立在系统坐标系下含关节间隙的机构动力学模型，基于并联机构的运动学约束特性分析，将各支链视为一个整体的刚性构件，将被动转动副之间的关节碰撞力由转换矩阵Ri等效到相应广义接触碰撞力fi处，则

(22)

4.2 含关节间隙并联机构的动力学模型

为进一步研究含关节间隙并联机构的广义驱动力的变化规律，本文采用非完整系统的拉格朗日方程法对含关节间隙的该并联机构进行动力学建模。

(23)

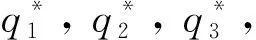
(24)

(25)

构件l1i,l2i,l3i和l4i在定坐标系O-XYZ中的质心坐标分别对时间t求导，并代入式(24)中，化简可得

(26)

将式(25)、式(26)代入非完整系统的Lagrange方程式(27)

(27)

经化简计算可得实现系统给定运动轨迹的广义驱动力的解析表达式，如式(28)～式(30)所示

(28)

(29)

(30)

式中，F1,F2,F3为含关节间隙并联机构与给定广义位移q1,q2,q3相对应广义驱动力的解析表达式。

5 数值分析

为验证上述理论分析的正确性，并进一步对该含间隙并联机构的运动学和动力学特性进行研究，需进行实例计算。设3-CPaRR并联机构的结构参数如表1(表中i=1, 2, 3 )所示，设机构的构件材料均质为碳素钢。表2给出了含间隙并联机构的动力学仿真参数。

表1 并联机构的结构参数

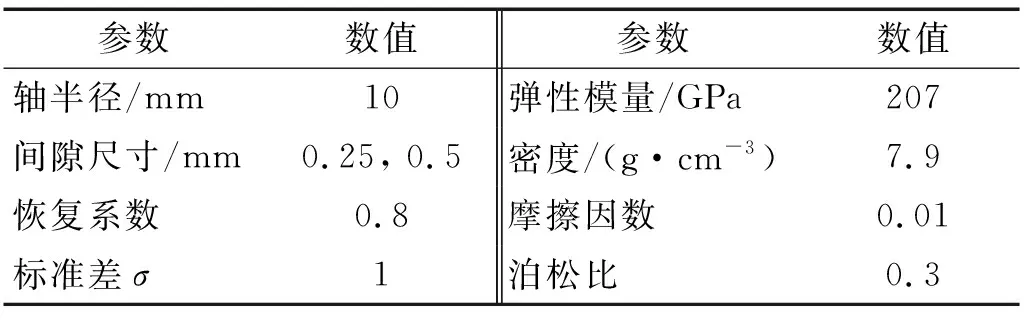
表2 含关节间隙并联机构的动力学仿真参数

设定系统任务运动规律，即动平台随时间的变化规律如下，同时，设定两种被动转动关节的间隙量分别为cr=ca=0.25 mm,cr=ca=0.5 mm。

(31)

为能清晰体现含关节间隙并联机构的动力学方程建模的计算过程，图7给出了含关节间隙并联机构动力学方程计算迭代过程。为降低计算难度，重点分析间隙引起的关节碰撞对机构的影响：① 为保证计算精度和计算效率，采用四阶龙格库塔法进行数值积分；②当关节元素判定为不接触碰撞时，为提高计算效率，可直接基于Lagrange方程法进行动力学建模。

计算结果如图8～图11所示。其中，在给定末端动平台运动规律后，图8和图9对比分析了在考虑两种关节间隙尺寸参数下实现系统给定运动轨迹等效圆

柱副Ai在定坐标系O-XYZ中沿X,Y,Z坐标轴方向的位移变化情况。图10和图11对比分析了在考虑两种关节间隙尺寸参数下实现系统给定运动轨迹驱动广义外力的变化情况。

图7 含间隙并联机构的动力学方程建模过程Fig.7 The calculation process of dynamic equation of parallel mechanism with joint clearance

图8 关节间隙量cr=ca=0.25 mm时，间隙关节的位移变化曲线Fig.8 The displacement variation of the joint with clearance when cr=ca=0.25 mm

图9 关节间隙量cr=ca=0.5 mm时，间隙关节的位移变化曲线Fig.9 The displacement variation of the joint with clearance when cr=ca=0.5 mm

图10 关节间隙量cr=ca=0.25 mm时，驱动广义外力变化规律Fig.10 The driving forces variation of the joint with clearance when cr=ca=0.25 mm

由图8～图11可知，可见间隙存在使得转动关节的关节元素在机构运转过程中发生高频接触碰撞，这些碰撞可引起机构振动，降低材料的疲劳极限，减少材料的使用寿命。其中，图8、图9给出了两种间隙量下该含关节间隙并联机构在给定动平台运动规律后，经运动学反解得到的驱动圆柱副Ai的位移情况，可见关节间隙对圆柱副的运动情况影响较大，其原因有：①关节间隙量相对并联机构结构尺寸较大;②并联机构的

图11 关节间隙量cr=ca=0.5 mm时，驱动广义外力变化规律Fig.11 The driving forces variation of the joint with clearance when cr=ca=0.5 mm

输入输出运动为完全解耦，该并联机构无过约束使得机构位移所受的间隙影响没有削弱。图10、图11给出了驱动圆柱副Ai相应的驱动外力的变化情况，因间隙的存在使得机构在碰撞过程中，广义驱动外力呈现高频大幅的震荡，震荡产生的冲击导致机械系统的非线性响应，使得该机构的动力学特性急剧退化。另外，可见随转动关节间隙量的增加，其振幅也随之增加，并联机构的碰撞和震荡情况愈加强烈。

参数μ作为正态分布概率统计模型的重要参数，其数学意义为随机变量的数学期望值，其值大小决定了正态分布概率的分布位置，考虑关节元素间的相对位置，本文定义以关节元素开始接触时的间隙值cr,ca作为定义数学期望值μ。为验证该定义的物理意义，本文取等效圆柱副A1为例，以标准正态分布的参数(即μ=0)为对照。给出了不同数学期望值μ下的间隙关节等效圆柱副A1的位移变化曲线和广义外力变化曲线，如图12、图13所示。

图12 不同参数μ下间隙关节的位移变化规律Fig.12 Displacement variation of the joint with clearance at different parameters μ

图13 不同参数μ下的驱动广义外力变化规律Fig.13 Driving forces variation of the joint with clearance at different parameters μ

由图12可知，当参数μ取值为0或cr,ca时，可见含间隙转动关节运动皆可达到最大碰撞冲击深度，即变化参数μ的取值并不影响关节元素间的最大间隙量。比较μ的不同取值可见，μ=0时的位移变化波动情况较μ=cr=ca时，波动情况较为平缓。其原因为：当定义μ=0时，即转动关节中心点随机集中分布于关节坐标系原点Cr处，而当μ=cr=ca时，转动关节中心点随机概率值集中分布于关节元素接触碰撞处附近。

由图13可知，图13(a)和图13(c)相对图13(b)和图13(d)的广义外力变化频率较高，其接触碰撞次数较多。同时也可见变化参数μ的取值不改变最大广义外力值，即并不影响最大接触碰撞力。

综上所述，μ值变化并不影响关节元素之间的最大间隙量和最大接触碰撞力，然而，接触间隙矢量值为μ=cr=ca值，接触碰撞频率较高，根据此值计算材料的疲劳极限和机构的使用寿命可以提前到达，工程应用预测更可靠。

6 结 论

(1) 本文分析了3-CPaRR并联机构的运动学规律，揭示了该机构在空间正交方向上的移动完全解耦特性，确定了支链末端转动关节为消极运动副，且该并联机构圆柱副可等效分解为驱动移动副和被动转动副。

(2) 基于运动学分析规律，提出以正态分布概率统计模型建立含间隙转动副在转动关节径向和轴向的运动学模型，进而建立了关节间隙支链运动学模型。然后基于Flores接触模型建立间隙关节法向接触力模型和修正的Coulomb摩擦模型建立了间隙关节切向接触力模型，并基于非完整Lagrange方程法建立了含间隙并联机构的动力学模型，通过实例计算详细分析并验证了含间隙并联机构运动学特性和间隙对系统动态响应的影响。

(3) 通过与标准正态分布模型对比，分析了定义关节元素开始接触时的间隙量为μ值时，更具有工程应用价值。