圆柱体涡激振动的高阶非线性振子模型研究

康 庄， 张 橙， 付 森， 徐 祥

(哈尔滨工程大学 深海工程技术研究中心，哈尔滨 150001)

涡激振动现象广泛存在于许多工程领域中，例如海洋油气勘探中的立管、桥梁悬索、天线等[1]。当一定流速的流体绕过柱形结构物时，会在其后方产生周期性的泄涡现象，漩涡的不断产生和脱落会对结构产生周期性变化的升力和阻力，使其发生横流向和顺流向的涡激振动，涡激振动是结构产生疲劳损伤的重要原因之一。

对圆柱进行涡激振动进行研究是对立管等柱形结构物涡激振动分析的基础，近些年大量研究者通过开展模型试验或采用CFD(Computational Fluid Dynamics)数值模拟以系统研究圆柱涡激振动中的诸多现象及产生机理等，如Govardhan等[2-6]等。这两种方法的研究内容较为丰富，但模型试验的成本较高，CFD数值模拟又较为复杂，特别是在高雷诺数情况下的数值模拟仍是一个难题，其目前还难以满足工程的实际需求，因此通过建立相应的数学模型并结合试验数据选取合适的经验参数来快速预报涡激振动的一些重要特性得到了广泛的关注。

Bishop等[7]最先提出了利用自激自限的Van der Pol方程来模拟涡激振动中流体对结构的升力作用。之后Hartlen等[8]对Bishop等的模型进行了改进，将结构振动的速度与Van der Pol方程进行耦合，其改进的模型是最早提出的尾流振子模型。在他们的研究基础上，Griffin等[9-11]都对尾流振子模型进行了研究并取得了一定的成果，这也使得尾流振子模型逐渐成为预报圆柱体涡激振动的最经典的模型。但他们的研究大多都只考虑了单自由度涡激振动，而涡激振动中的流向振动具有其高频特性及对横向振动产生的耦合作用，在涡激振动中所产生的作用是不可忽视的，特别是对于较低质量比的结构物。

Srinil等[12]通过采用两个duffing方程和两个Van der Pol方程来分别模拟结构振子和流体振子的运动，但其得到的脉动升力与脉动阻力之间不存在联系，难以充分考虑流向振动与横向振动的耦合作用。秦伟等[13]利用离散点涡的方法推导了圆柱涡激振动所受的流体力，再结合线性振动方程与经典尾流振子方程，得到了一种可以计算双自由度涡激振动相关特性的模型，但其建立的双自由度涡激振动预报模型中的线性化假设过多，使得最后预报结果的精度仍有提高的空间。

为定性且定量预报圆柱双自由度涡激振动幅值响应、频率及运动轨迹等重要特性，本文首先基于拉格朗日第二类动力学方程推导了双自由度涡激振动方程，将传统的线性结构振动方程改为了非线性振动方程以提高预报精度；然后利用毕奥-沙伐定理、圆定理以及非定常流动的卜拉休斯合力公式推导了圆柱所受的脉动流体力，得出了脉动升力与脉动阻力间的数学关系，减少了方程数量，有利于提高计算效率；最后引入一个包含五阶气动阻尼项的高阶Van der Pol方程来模拟流体振子，此方程可以更好地模拟迟滞现象以及低质量比条件下振动幅值的超上端分支。在此基础上提出了一种用以准确预报圆柱双自由度涡激振动幅值等重要特性的高阶非线性振子模型，然后对模型在不同质量比和阻尼比下进行了验证与分析，并对模型中各参数进行了敏感性分析，系统研究了该模型的预报特点。

1 高阶非线性振子模型的建立

1.1 非线性结构振动方程

结构的涡激振动具有很强的非线性特征，以弹性支承方式来固定圆柱时一般会用到多个弹簧，特别是在双自由度的涡激振动中，圆柱带动弹簧运动时已经不再是满足线性条件。圆柱双自由度涡激振动的模型，如图1所示。四个弹簧的耦合作用使其运动表现出非线性特征。

对于图1中的振动模型，设四个弹簧的弹性系数均为k，其原始长度均为a，圆柱位于中心的平衡位置时各弹簧均为原长状态，则对于该系统，其动能为

(1)

势能为

图1 圆柱双自由度涡激振动的模型示意图Fig.1 Schematic diagram of VIV of a cylinder with two DOF

(2)

则拉格朗日函数为

(3)

(4)

式中:qj分别为X和Y; 对式(4)求解即可得到X和Y方向的系统运动方程

(5a)

(5b)

可以发现式(5a)和式(5b)是非线性耦合方程，其非线性主要体现在弹簧的几何非线性上，此公示较为复杂，难以直接求解，需要对其进行化简。应用二元函数的泰勒展开公式对上式中的非线性项进行三阶展开，得到

(6a)

(6b)

同时，考虑到kx=ky=2k，m=ms+ma，c=cs+cf。

(7a)

(7b)

可以发现改进的非线性结构振动方程包含X3，XY2，Y3以及YX2，其中X3和Y3主要模拟振动的轴向几何非线性，XY2和YX2主要模拟横向和流向振动的耦合非线性，并且本文改进推导的方程将轴向几何非线性参数和耦合非线性参数联系了起来，减少了非线性项中的经验参数，有利于提高计算的精度和减小计算量。

1.2 流体力推导

将贴近圆柱表面的一层区域称为近壁控制域，近壁控制域以外的区域称为尾涡域，如图2所示。设在某一时刻近壁控制域有m个控制涡，尾涡域有n个稳定点涡，则整个流体域内一共有N=m+n个离散点涡。

图2 圆柱周围流场划分示意图Fig.2 Schematic diagram of flow division around the cylinder

由N个点涡与均匀来流叠加，并结合圆柱壁面映像—圆定理可得到图2中流场复势为

(8)

由非定流动的卜拉休斯合力公式可知圆柱所受流体力为

(9)

(10a)

(10b)

式中：xk和yk为第k个涡位置与直径D的比值，即无量纲化的位置。

对于上式中的方括号部分，将其分别记为fD1和fL1，在控制域内，点涡的平均速度可以忽略不计，所以只有尾涡域的点涡对其产生作用。在尾涡域中，认为uk=U，vk=0，即点涡沿顺流向运动，同时由于尾涡域中点涡到圆心距离的平方增加很快，并且点涡的横向位置yk较小，将其近似为0，则fD1和fL1可以近似表达为

fD1=0

(11a)

(11b)

对于尾涡域中的总涡量Γn(t)，由于正向和反向点涡交替进入尾涡域，其总涡量表现为周期性地增大和减小的状态，并且其频率为泄涡频率ωst，峰值为Γ，出于简化的目的，用余弦曲线来描述这一过程，则

fD1=0

(12a)

fL1=ρΓUcos(2πωstt)

(12b)

(13a)

(13b)

式中：xC和yC为等效控制涡质心的无量纲位置；考虑到yC在y轴的正负半轴振动，而xC只在x轴正半轴作微幅变化，因此只考虑yC的作用。

根据涡的生灭原理，整个流场的涡量是保持不变的，因此等效控制涡的涡量变化与尾涡域的涡量变化过程相反，因此可得到

ΓC=-Γcos(2πωstt)

(14)

进一步得到

(15)

等效控制涡的大小与尾涡域的涡强大小相反，并且等效控制涡取代的是刚进入尾涡域的点涡的位置，因此yC在尾涡域正向点涡与反向点涡的位置间交替变换，也可以用余弦函数来近似表示其变化过程，并且认为其幅值与稳定点涡的涡强有关，但由于其具体大小未知，需要引入由试验确定的经验参数α，进而可以将其表示为

(16)

进一步可得到

(17a)

fL2=0

(17b)

结合推导得到的fD1，fL1，fD2以及fL2，再引入无量纲尾流变量q=2CL/CL0，CL0为参考升力系数，它表示固定圆柱在流场中所受的升力，结合FL=ρDU2CL/2，得到4Γcos(2πωstt)=UDCL0q，因此FX和FY为

(18a)

(18b)

1.3 Van der Pol方程的高阶改进

经典尾流振子模型利用Van der Pol方程来模拟尾流振子的运动，Facchinetti等[14]在其研究中认为Van der Pol方程的激励项与横流向振动的加速度有关，Dolatabadi等[15]研究发现经典尾流振子模型可以较好地预报高质量比情况下的圆柱涡激振动响应，但在低质量比条件下，经典尾流振子模型预报得到的值要偏小，因此有必要对其进行改进。

本文根据Landl[16]提出的一种高阶Van der Pol方程模型，结合Farshidianfar对单自由度涡激振动的高阶尾流振子模型的研究，对经典尾流振子模型进行了高阶改进。Landl的高阶模型包括了一个Van der Pol阻尼项和一个五阶气动阻尼项，具体公式为

(19)

式中：Ωr为结构振动频率；α′,β′,λ′和b为经验参数，需要根据不同的具体问题而选择。将其转化为Van der Pol方程的形式，令α′=-ε，β′/ε=-β，λ′/ε=λ，再结合Van der Pol方程可以得到

(20)

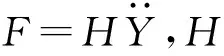
可以发现该模型方程与经典Van der Pol方程是相通的，当β=1，λ=0时此方程便是经典Van der Pol方程，此方程通过调整β和λ的值便可适当地增加Van der Pol振子的振动幅值，可以有效地改善经典Van der Pol方程难以准确模拟出低质量比条件下的高振动幅值情况。

1.4 耦合非线性振子方程

(21a)

(21b)

(21c)

式中：M=CD0/(32π2St2μ);N=CL0/(16π2St2μ);ξ=cs/(2msωn)为圆柱的黏性阻尼比；ωn为固有频率，μ为质量比参数，μ=(ms+ma)/ρD2;δ=ωn/ωst为频率比;γ=cf/(4πSt)，根据Ogink等[17]的研究将其取为0.5；η为圆柱振动的几何非线性参数，本文通过与试验结果拟合将其取为0.2；h为无量纲形式的耦合参数，根据Facchinetti等的研究将其取为12；ε为Van der Pol方程的阻尼参数，与圆柱的质量比有关，本文通过与大量试验数据进行拟合给出了其确定曲线，如图3所示；β和λ为Van der Pol振子的非线性参数。CL0和CD0分别为参考升力系数和参考脉动阻力系数，本文参考Blevins等[18-19]的研究，将CL0和CD0分别取为0.3和0.2。

图3 由质量比得到的参数ε值拟合曲线Fig.3 Fitting curve of ε based on mass ratio

对于β和λ，参考Stappenbelt等[20]对非线性方程的求解方法，在无外力扰动时，高阶Van der Pol方程可写为

(22)

该方程的解可分为线性部分u(t)和非线性部分εv(t)，忽略其中的高阶非线性部分，可得到

q(t,ε)=u(t)+εv(t)+…

(23)

将式(23)代入式(22)，对其中的线性部分和非线性部分分别求解，可得到

(24)

代数运算求解式(24)得到

u=q0cosωt

(25a)

(25b)

(26)

可以发现公式中的自变量有两个，为β和λ，通过合理选择β和λ的值便可达到改变q0从而改变流体振子振动幅值的目的，进而影响结构振子的振动幅值，本文通过与试验数据进行拟合，将β取为0.25，λ取为0.008。

2 算例验证与分析

2.1 圆柱双自由度涡激振动算例验证

以Jauvtis等 的圆柱双自由度涡激振动模型试验为参考，圆柱相关参数如表1所示。

表1 圆柱各项参数

利用变步长四阶龙格-库塔法对高阶非线性振子模型进行求解，得到了圆柱无量纲振幅、频率以及运动轨迹，并与试验结果进行对比，如图4～图6所示。

(a)横向振动

(b)流向振动图4 圆柱振动幅值响应对比Fig.4 Comparison of the amplitude of the cylinder

通过对比分析图4(a)的横向振幅曲线可以发现，Ur>4之后，圆柱横向涡激振动逐渐进入共振阶段，其振幅显著增加，Ur>8后，开始渡过共振阶段，幅值又大幅减小，这与Williamson的试验结果在总体趋势上是一致的，并且对于涡激振动幅值响应预报中最重要的“上端分支”和“超上端分支”，数值结果与试验结果吻合较好，得到的最大振动幅值约为1.5D，与试验结果非常接近。但也可以发现数值模型没有准确模拟出振动幅值中的“下端分支”，这主要是由于本文将耦合参数ε选为仅和质量比有关的常数，如果将其再与约化速度联系起来即可调整下端分支的形状，这在今后可以进行进一步的研究。

对于图4(b)的流向振幅曲线，可以发现在Ur=2.5附近处，流向振动出现了流向的共振，而后其振幅又迅速减小，紧接着由于横向振动对流向振动的耦合作用，大幅值的横向振动导致流向振动也开始大幅增加，之后由于横向振动渡过共振，流向振动幅值也相应大幅减小。数值模型得到的流向振幅趋势与最大值都与试验结果吻合良好，再结合其对横向振动幅值响应的合理预测，表明本文的非线性振子模型可以定性并定量地预测圆柱双自由度涡激振动幅值特性。

图5 圆柱横向振动无量纲频率对比Fig.5 Comparison of the cross-flow dimensionless frequency

对于图5的横向无量纲振动频率，可以发现计算结果在Ur大约为4～9发生了锁定现象，而在其他Ur下则满足斯特劳哈尔关系，这与试验数据及相关的理论研究基本一致，但由于数值模型未能准确模拟出Wiiliamson试验中横向振动的“下端分支”，导致其在Ur较大时与其试验结果出现一定差别，总的来说，数值模型基本能够定性反应圆柱涡激振动的频率特性。

图6 圆柱涡激振动运动轨迹图Fig.6 Trajectory of the vortex-induced vibration of the cylinder

图6给出了计算得到的各约化速度下圆柱的运动轨迹，在流速较低时，流向振动幅值相对横向幅值较大，圆柱运动轨迹为扁平或标准的“8”字形，但是其总体运动比较小；随着流速的增大，横向振动逐渐进入共振状态，幅值显著增加，圆柱轨迹表现为拉长的“8”字形，并且逐渐表现出向右倾斜的趋势，Ur为8～9附近轨迹形状接近月牙形；随着的流速的持续增加，横向和流向振幅均大幅减小，圆柱运动轨迹又变为了缩小的“8”字形，并不断在变瘦变小，这些轨迹变化规律与目前的涡激振动研究结果一致。

总的来说，通过与Williamson的试验结果对比，发现本文提出的高阶非线性振子模型能够较为准确地模拟出圆柱涡激振动幅值响应、频率及运动轨迹特性，可以为快速预报结构物涡激振动特性研究提供一定的参考。

图7 不同质量比下圆柱横向振动幅值响应对比Fig.7 Comparison of cross-flow amplitude of the cylinder with different mass ratios

2.2 质量比对振动的影响

质量比是影响圆柱涡激振动特性的一个重要因素，本文将参考Stappenbelt等开展的圆柱双自由度涡激振动试验结果，将质量比分别选为2.36,3.68,5.19,6.54,8.76及10.63，阻尼比选为0.006，进行圆柱双自由度涡激振动特性预报。

图7为不同质量比圆柱涡激振动横向振幅的计算结果与Stappenbelt的试验结果，Increase和Decrease分别表示加速和减速模拟，可以发现在不同质量比下，两种结果在趋势上能够保持一致，并且计算的最大幅值与试验值差别不大，另外，可以发现随着质量比的增加，圆柱横向振动的最大幅值在不断减小，锁定区间也在减小，振子模型预测的迟滞区间在不断变大，这是因为随着质量比的增加，耦合参数ε也在增加，使模型方程的非线性增强，导致迟滞区间变大。

对比分析图8中流向振动幅值响应曲线，发现各质量比条件下的计算结果也与试验结果在趋势上一致，并且计算的最大幅值在总体上与试验值基本吻合，但在质量比为2.36时过度地预测了圆柱流向振动最大幅值，这是由于在低质量比条件下本文选取ε时参考的是Willamson试验，而Stappenbelt等试验在低质量比条件下的流向幅值结果要比Willamson试验结果偏小，导致此时的模型预测出现差别。另外，随着质量比的增加，横向振动对流向振动的耦合作用在减弱，使得其第二个峰值不断减小，与横向振动类似，流向振动迟滞区间也随质量比的增大而增大。

另外，为分析质量比对圆柱在幅值分支突变附近的运动轨迹的影响，在图9中给出了不同质量比下Ur为6.0, 8.5, 10.0时的运动轨迹曲线。可以发现在Ur=6.0时，随着质量比的增加，其轨迹的“8”字形变得越细，这是因为质量比增加使得横向振动对流向振动的耦合作用降低；Ur=8.5时，低质量比下圆柱轨迹为“月牙”形，随着质量比的增加其轨迹形状大幅减小，并且没有呈现出“月牙”形，这是因为随着质量比增加，锁定区间在减小，在Ur为8.5时其振动已跳出锁定区；Ur=10时，各质量比下圆柱轨迹又变为“8”字形，并且质量比越高，“8”字形越小。

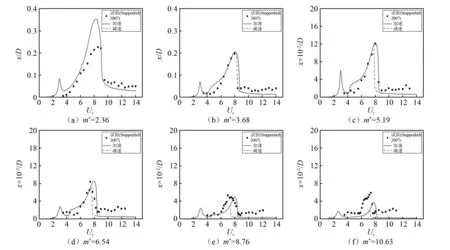
图8 不同质量比下圆柱流向振动幅值响应对比Fig.8 Comparison of in-line amplitude of the cylinder with different mass ratios

图9 不同质量比下圆柱运动轨迹对比Fig.9 Comparison of the trajectories of the cylinder with different mass ratios

2.3 阻尼比对振动的影响

阻尼比是另一个影响圆柱涡激振动特性的参数，本文参考Blevins等开展的不同阻尼比下的圆柱双自由度涡激振动试验结果，对质量比为5.4，阻尼比分别为0.002, 0.02, 0.05, 0.1, 0.2及0.4的圆柱涡激振动进行数值模型预报，并与试验结果进行了对比。

图10为各阻尼比下圆柱的横向幅值响应曲线，可以发现计算结果的曲线趋势与最大值与试验结果具有较好的吻合度，随着阻尼比的增加，横向振动幅值显著降低，迟滞现象也不再明显，但其锁定区间的大小变化不大。

图11为各阻尼比下圆柱的流向幅值响应曲线，由于高阻尼比下流向振幅非常小，本文只给出了阻尼比为0.002和0.02时的对比结果；由图11可知计算结果与试验结果在趋势上能够保持一致，但计算得到的最大幅值要比试验值偏小一些，并且随着阻尼比的增加，流向振幅的最大值随之减小。

总的来说，各阻尼比条件下的模型计算幅值响应与试验结果基本吻合，再次验证了本文模型应用的正确性和广泛性。

同样，在图12中给出了Ur为6.5和8.5时的圆柱运动轨迹曲线，可以发现Ur为6.5时，随着阻尼比的增大，运动轨迹逐渐由“8”字形变为“月牙”形，并且轨迹尺寸大幅减小，这是由于阻尼比较大时其振幅达到峰值时的Ur较小，对应的“月牙”形轨迹会提前出现；Ur为8.5时，其轨迹也随阻尼比的增加而向“月牙”形过渡，但其尺寸大小的变化较为缓慢，这是由于Ur为8.5时开始跳出锁定区间，阻尼比对其振幅的影响较小。

图10 不同阻尼比下圆柱横向振幅对比Fig.10 Comparison of cross-flow amplitude of the cylinder with different damping ratios

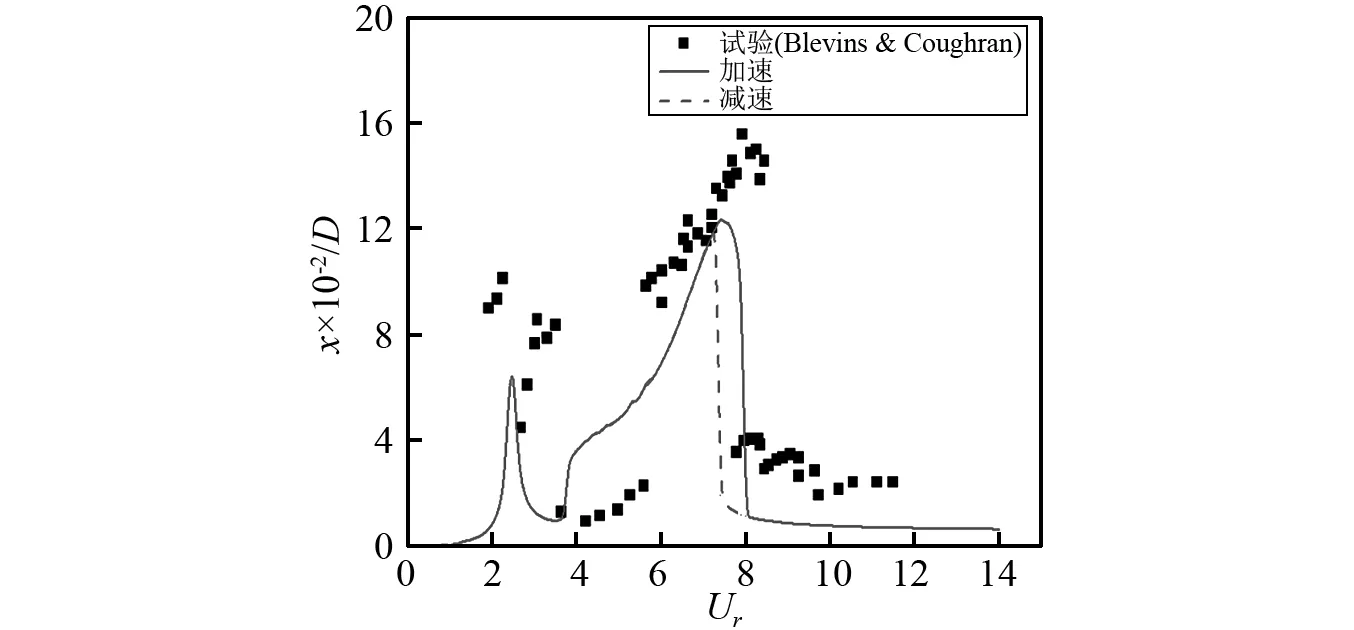
(a)ξ=0.002

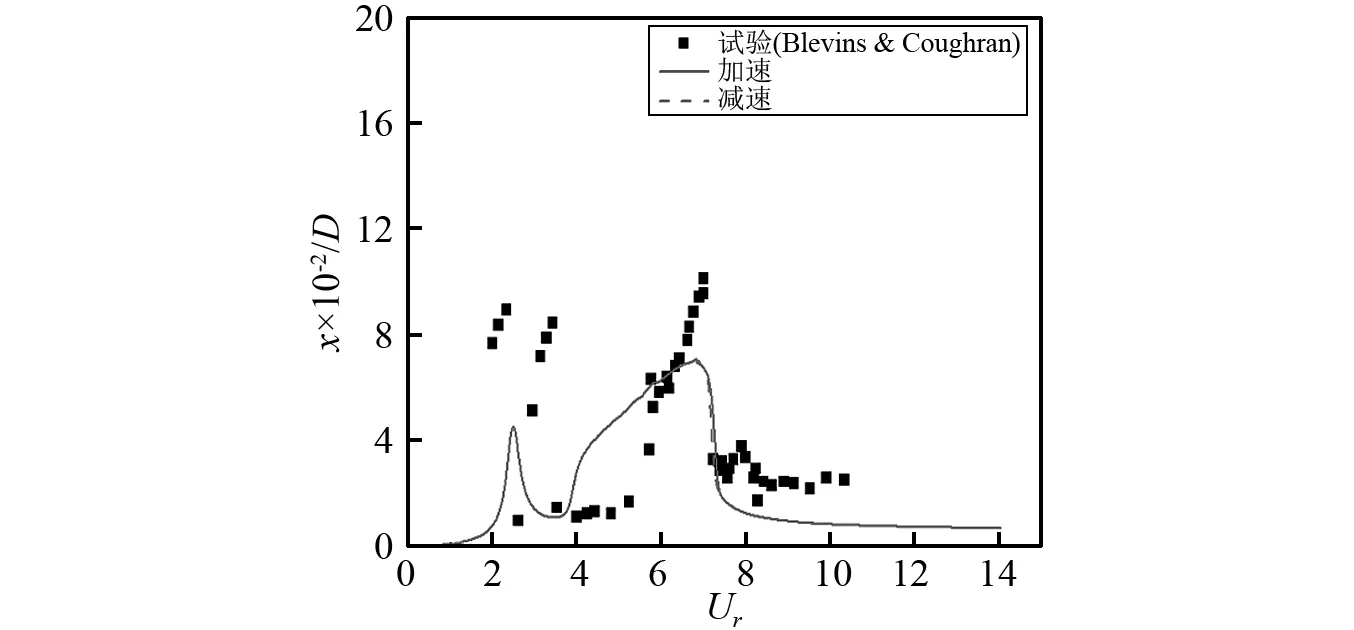
(b)ξ=0.02图11 不同阻尼比下圆柱流向振幅对比Fig.11 Comparison of in-line amplitude ofthe cylinder with different damping ratios

(a)Ur=6.5

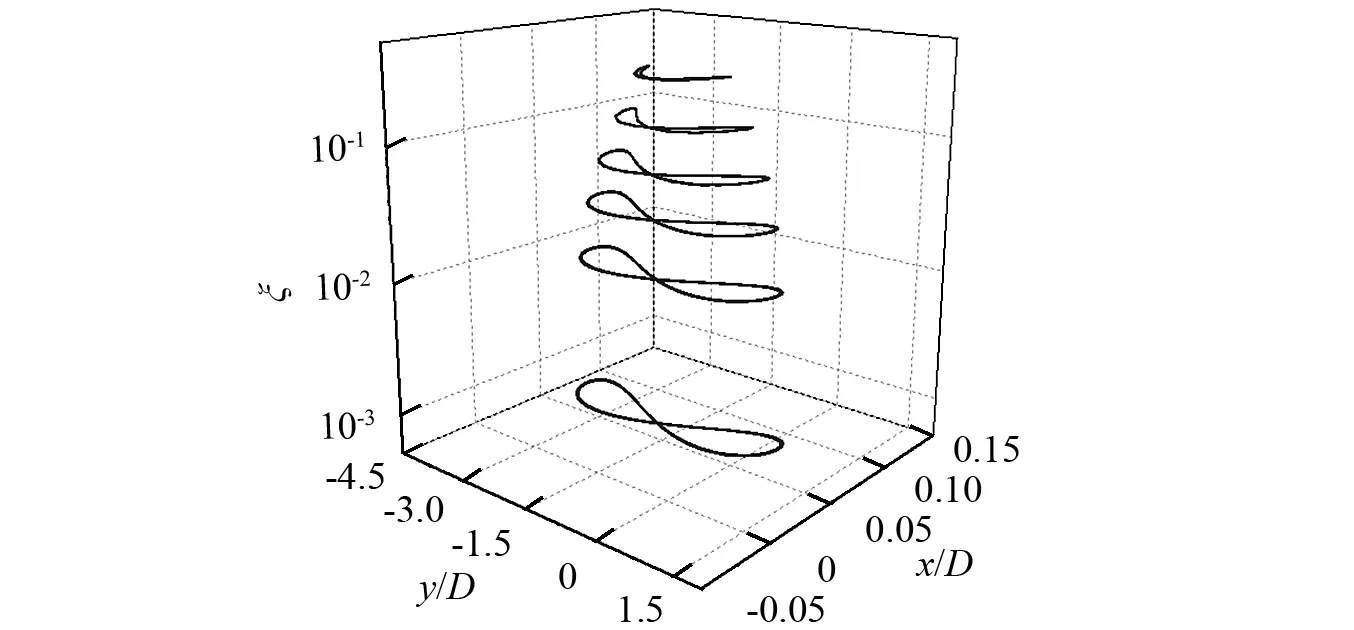
(b)Ur =8.5图12 不同阻尼比下圆柱运动轨迹对比Fig.12 Comparison of the trajectories ofthe cylinder with different mass ratios

3 模型参数敏感性分析

本文模型主要引入了三类经验参数，分别为几何非线性参数η、耦合参数h和ε以及流体振子阻尼参数β和λ，为全面分析其对预报效果的影响，需要对其敏感性进行研究。

3.1 几何非线性参数分析

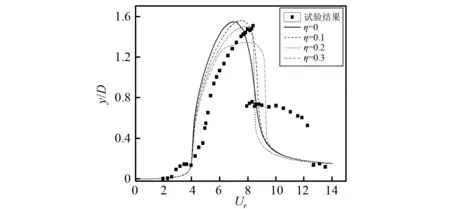
将模型的几何非线性参数η分别取值为0, 0.1, 0.2和0.3进行圆柱双自由度涡激振动计算，圆柱参数仍取Jauvtis等的圆柱双自由度涡激振动模型试验参数，质量比为2.6，阻尼比为0.005。将模型预报结果与试验结果进行对比，如图13所示。

(a)横向振动

(b)流向振动图13 不同几何非线性参数下圆柱振动幅值响应对比Fig.13 Comparison of the amplitudes withdifferent geometric nonlinear parameters

由图13可知，随着参数η的增加，横向和流向振幅曲线形状都发生了较为明显的变化。对于横向振动，η增加时，曲线达到峰值时的Ur有所增大，并且其峰值大小各不相同，η为0.1和0.2时预报得到的最大幅值均与试验结果较为接近，但η为0.2时的峰值对应的Ur更接近试验值。对于流向振动，其形状随η的变化较为剧烈，随着η的增加，其第二个峰值的大小也在增加，但第一个峰值大小基本没有变化，可见η对流向振动的影响主要体现在横向对流向的耦合作用方面，并且η为0.2时流向幅值响应结果与试验值吻合最好。

总的来说，随着η的增加，横向最大振幅在减小，而流向最大振幅在增加，并且流向幅值响应曲线形状受η的影响更大，通过分析选择几何非线性参数的大小可以实现对横向和流向振动耦合作用的合理配置。

3.2 耦合参数分析

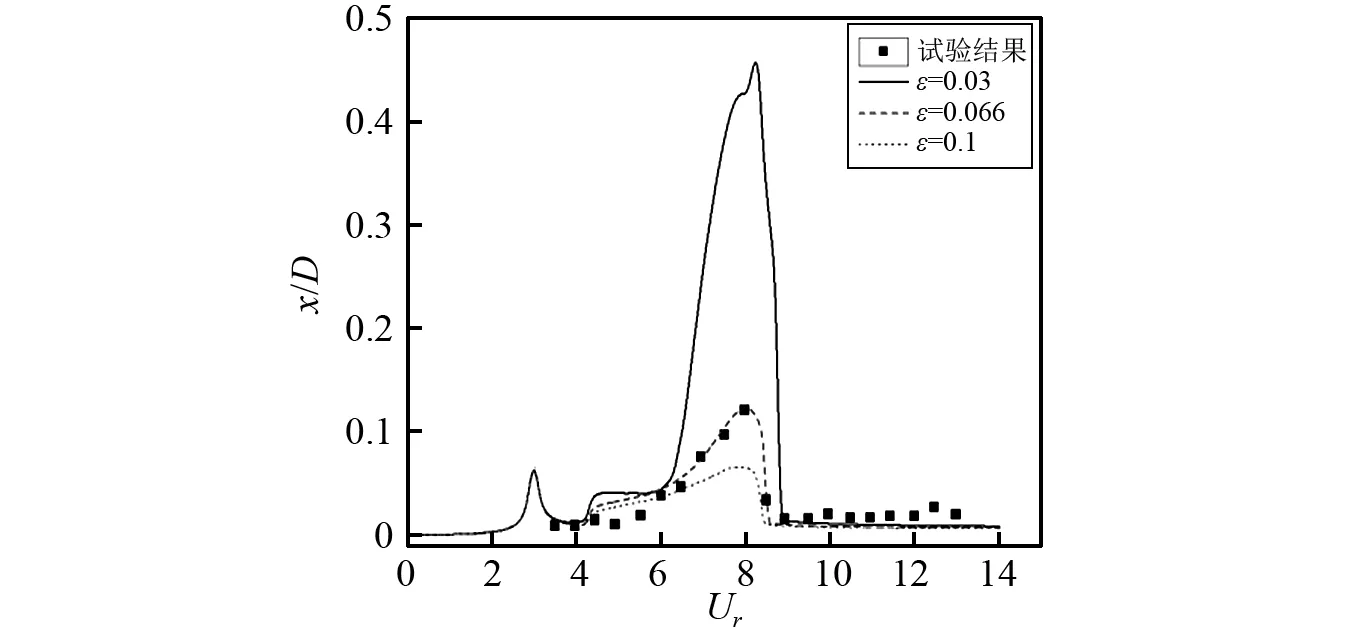
首先对参数ε进行分析，以Stappenbelt等的试验数据为参考，在质量比为5.19，阻尼比为0.006的条件下，将ε分别取为0.03， 0.066和0.1进行计算，将得到的圆柱幅值响应曲线与试验结果进行对比，如图14所示。

由图14可知，随着参数ε的增加，横向振动和流向振动的最大幅值都在不断减小，并且锁定区间宽度也出现微小幅度的减小。对于横向振动，其峰值所对应的Ur值随ε的增加而减小，三组参数下所得结果的差别主要体现在锁定区域内，ε取0.066时模型预报结

(a)横向振动

(b)流向振动图14 不同参数ε下圆柱振动幅值响应对比Fig.14 Comparison of the amplitudes with different ε

果与试验结果吻合最好；对于流向振动，其幅值曲线形状对ε的变化更敏感，表明随着ε的增大，横向振动对流向振动的耦合作用更强，使其变化更大。总的来说，参数ε的作用主要是调节横向与流向振动的锁定区域内幅值峰值大小及它们之间耦合作用的大小。

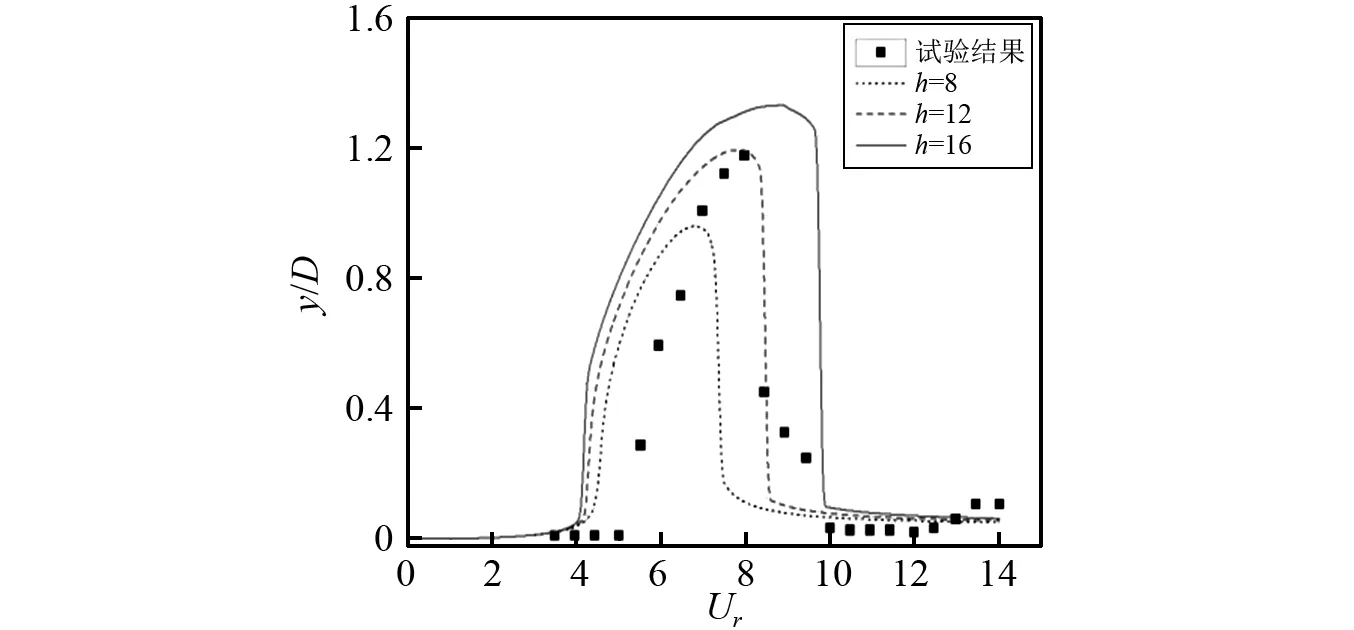
对于参数h，仍以Stappenbelt的试验参数为基础，将其分别取值为8,12和16，将模型预报结果与试验结果进行比较，如图15所示。

(a)横向振动

(b)流向振动 图15 不同参数h下圆柱振动幅值响应对比 Fig.15 Comparison of the amplitudes with different h

由图15可知，参数h不仅影响最大振幅的大小，而且也影响锁定区间的宽度，随着参数h的增加，横向和流向振动的最大幅值都有所增加，其锁定区间的宽度也有显著增加。通过与试验值进行比较，发现h为12时模型预报的最大振幅、锁定区间宽度以及曲线形状等能够与试验结果吻合良好，其他取值均出现较大差别，这与Facchinetti等的研究结果一致。

3.3 流体振子阻尼参数分析

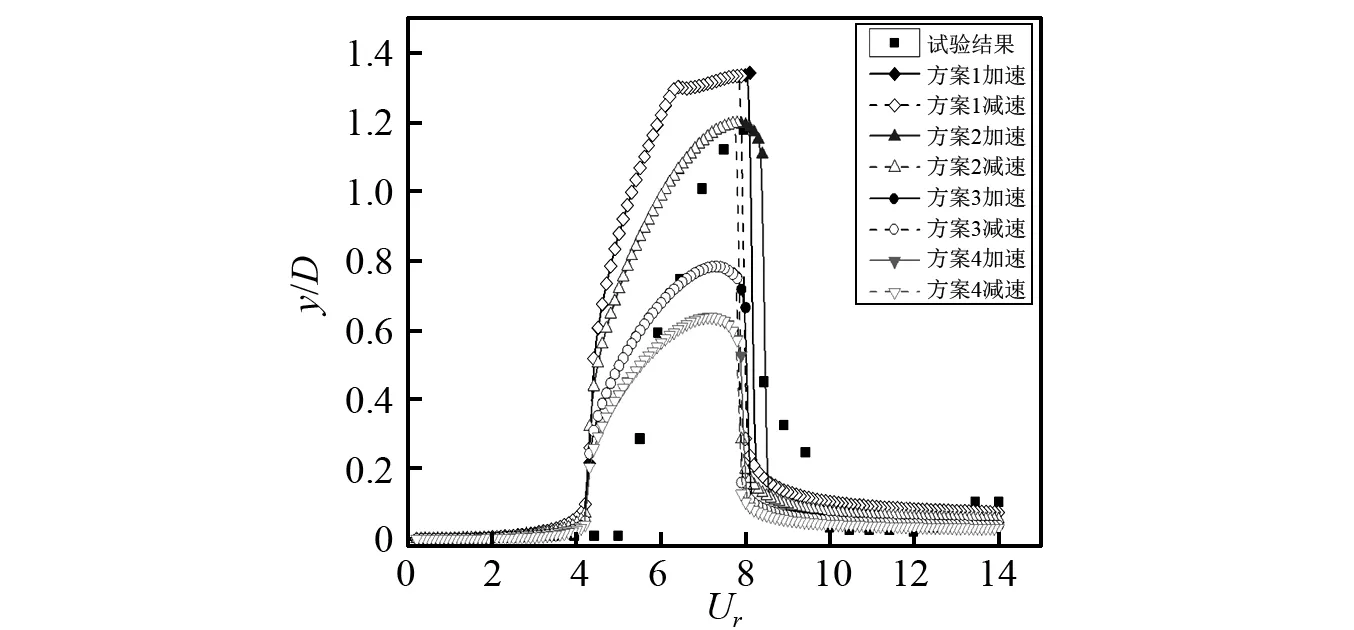
对于阻尼参数β和λ，圆柱质量比仍为5.19，阻尼比为0.006，依据“1.4”节中介绍的参数确定方法选择4组参数β和λ，分别编号为方案1～方案4，具体见表2，考虑到参数β和λ对迟滞区间有一定的影响，分别采用匀加速和匀减速两种条件进行计算，将各方案的计算结果与试验结果进行比较，如图16所示。

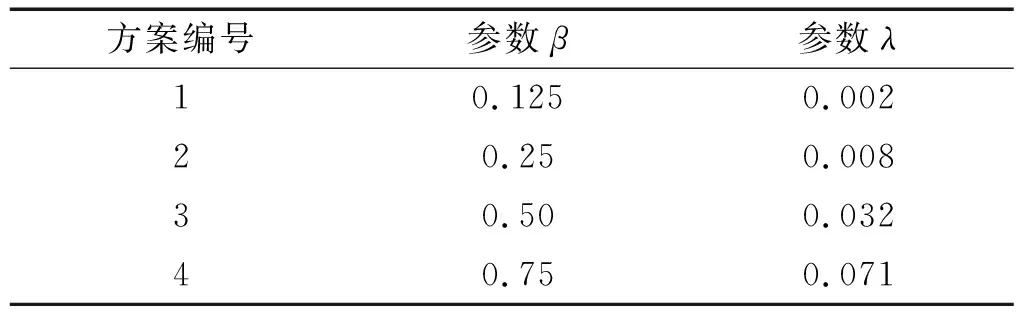
表2 阻尼参数选择方案

(a)横向振动

(b)流向振动图16 不同阻尼参数方案的圆柱振动幅值响应对比Fig.16 Comparison of the amplitude with different damping parameter schemes

对比分析横向振动幅值曲线，可以发现方案1～方案4的最大振动幅值依次递减，但其锁定区间和迟滞区间的宽度经历了先增后减的过程，其中方案2的锁定区间和迟滞区间最大；同样，在流向振动幅值曲线中也出现了类似的结果，而且流向振动不仅第二个峰值在发生变化，第一个峰值也有所区别，表明流向振动第一峰值的大小对流体振子阻尼参数的变化较为敏感，可以通过合理改变流体振子阻尼参数的大小来实现对其第一峰值的调整。将各方案得到的曲线与试验值比较，发现方案2的结果与试验结果拟合较好，表明本文所选择的阻尼参数β为0.25，λ为0.008的参数组合是合理的。

4 结 论

本文通过将非线性的结构振子方程和高阶Van der Pol方程进行耦合，并基于离散点涡理论推导了脉动升力和阻力，提出一种可以定性定量预报圆柱双自由度涡激振动幅值、频率及轨迹等重要特征的高阶非线性振子模型，然后对模型进行了算例验证，并分析了不同质量比和阻尼比下的振动特性，最后对模型中的三类参数进行了敏感性分析，得出以下结论：

(1)应用本文提出的高阶非线性振子模型计算得到的低质量比圆柱振动幅值、频率等特性与Williamson的试验结果吻合良好，并且得到的圆柱运作轨迹变化规律与现有研究一致，表明本文模型可以较为准确地预报低质量比圆柱涡激振动重要特性，验证了模型在低质量比条件下应用的正确性。

(2)在不同质量比和阻尼比下的模型预报幅值响应结果能够与Stappenbelt等的试验结果基本保持一致，并且发现质量比和阻尼比对圆柱横向和流向振动幅值及运动轨迹等特性有较大的影响，表明本文的高阶非线性振子模型可以用于预报不同质量比和阻尼比柱形结构物的双自由度涡激振动重要特性，验证了其应用的广泛性。

(3)通过采用控制变量法改变模型中的几何非线性参数η、耦合参数ε与h以及流体振子阻尼参数β与λ，对计算结果进行对比分析，发现参数η对横向和流向振幅都有所影响，通过分析选择η的大小可以实现对横向和流向振动幅值的合理配置；参数ε的作用主要是调节横向与流向振幅峰值及它们之间耦合作用的大小，而参数h不仅影响最大振幅的大小，而且也影响锁定区间的宽度；参数β和λ除了可以调节横向和流向幅值峰值的大小以外，还影响着迟滞区间的大小。另外，在对各参数进行对比分析的过程中也发现本文所选取的参数可以更加准确地预测出圆柱涡激振动的幅值特性，表明本文模型参数的选择合理可行。

总的来说，相比于经典尾流振子模型，本文的高阶非线性振子模型更加全面地考虑了双自由度涡激振动中的非线性特征，并且建立了脉动升力和脉动阻力的数学关系，在一定的质量比和阻尼比范围内的预报精度较高，可以为此范围内的海洋柱形结构物双自由度涡激振动特性的快速预报提供一定的理论支持。