抑制模态混叠的HHT结构模态参数识别方法研究

2018-09-28练继建荣钦彪董霄峰王鸿振

振动与冲击 2018年18期

练继建，荣钦彪，董霄峰,3，王鸿振，刘卓

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；3.天津大学前沿技术研究院有限公司，天津 301700)

希尔伯特-黄变换(Hilbert-Huang Transform，HHT)是Huang等[1-2]提出的用于处理非线性、非平稳信号的时频分析方法，是由希尔伯特变换(Hilbert Transform，HT)和经验模态分解(Empirical Mode Decomposition，EMD)两部分组成[3]。HT要求信号在任何时间点上只有唯一的“窄带”频率值，EMD能将非线性、非平稳的信号转化分解成多个本征模态函数(Intrinsic Mode Function，IMF)，IMF具备的条件恰能满足HT分析要求。因此，EMD拓展了HT方法的应用[4-5]。目前，HHT已在故障诊断[6]、医学、爆破、地震等非线性信号分析领域普及应用[7-8]。

EMD是HHT结构模态参数识别的基础，IMF质量好坏关系后续HT模态参数识别的精度，而模态混叠很大程度上影响IMF的分解质量[9]。造成模态混叠的根本原因表现在密集模态相互作用和间断事件干扰两个方面。针对密集模态互相作用造成的模态混叠：孙伟峰等[10]提出了使用增加IMF筛选迭代次数和改进掩蔽信号的方式，并以仿真试验证明了方法的有效性；肖瑛等[11]认为模态混叠的根源是各阶IMF间不完全正交，提出在EMD分解的过程中加入解相关的算法解决模态混叠问题；胡维平等[12]使用改进的屏蔽信号来限制分解信号带宽，进而解决密集模态相互作用造成的模态混叠；黄天立等[13]通过波组信号改变了相邻模态频比，进而实现EMD对密集模态的有效分解。针对因间断事件干扰造成的模态混叠：Wu等[14-15]提出总体平均经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)，能有效平滑信号中存在的间断事件提高IMF的分解质量，但会遗留部分辅助残余噪声；胡爱军等[16]提出在原始信号中加入辅助高频谐波信号，试验表明高频谐波能有效抑制间断事件的影响；Yeh等[17]提出了互补总体平均经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)，其本质是对EEMD的改进，在有效抑制间断事件对分解影响的同时较好的消除辅助残余噪声。

实测信号易受噪声干扰且大多被测结构的刚度和质量是突变的，这造成实测信号往往既包含密集模态也存在间断事件。对于模态混叠，以往研究主要围绕密集模态或间断事件进行单方面研究，鲜有研究考虑两方面因素的综合作用。针对上述问题，本文提出基于CEEMD分解与信号调频(Frequency Modulation，FM)结合的改进模态分解方法，并将改进方法应用于HHT模态参数识别中。针对仿真试验与实际水利工程坝体信号，改进HHT法在避免模态信息丢失的同时提高了模态参数识别的精度。

1 模态混叠

1.1 间断事件与CEEMD分解

间断事件是指：高频小幅值信号或脉冲干扰。通过时频平面可以形象的说明间断事件造成模态混叠的原因，信号存在间断事件时的时频平面，如图1所示。

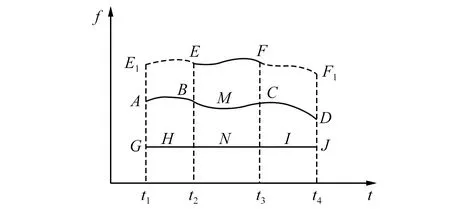
图1 含间断事件的时频平面Fig.1 Time-frequency plane with intermittent events

时频平面纵轴表示频率，横轴表示时间，EF代表信号中存在的间断事件。理想情况下，希望经过传统EMD分解获取复合在信号中的EF，ABMCD和GHNIJ3个IMF分量。但实际传统EMD分解总是从高频到低频依次将IMF分解出来，因此实际的分解结果为ABEFCD，GHBCIJ和HNI，可以看出分解误差具有传递性。相比传统EMD分解，CEEMD分解向含间断事件的信号中添加正负成对的高斯白噪声，借助添加噪声频率均匀分布的特征，使分解信号在各频率尺度上具备连续性，进而抑制间断事件对分解过程造成的影响。辅助高斯噪声的添加，使原本间断的信号在各频率尺度上具备了连续性。间断信号EF在加入辅助噪声后变为E1EFF1，高频间断信号会被分解到首阶高频IMF中，不会影响后续IMF的分解。CEEMD分解本质上仍以EMD分解为基础，具体可通过以下步骤实现[18]：

步骤1向待分解信号S加入m组正负成对的高斯白噪声N，得到2m组添噪信号

(1)

式中：M1和M2分别为加入正负高斯白噪声后的添噪信号。

步骤2对M1和M2中的每一个添噪信号进行EMD分解，则第i个添噪信号分解后得到的第j阶模态分量为IMFij。

步骤3计算添噪信号各阶模态分量的加总平均，得到最终模态分量IMFj。

(2)

下文通过仿真信号分析间断事件造成模态混叠的原因，仿真信号x(t)为两个单一频率余弦信号的叠加。

x(t)=x1(t)+x2(t)

(3)

x1(t)=cos(2πt×3)

(4)

式中：x2(t)为频率为45 Hz，幅值为0.1的高频小振幅间断信号。x(t)在EMD分解过程中，首阶IMF筛选3次时的极值包络曲线如图2所示。

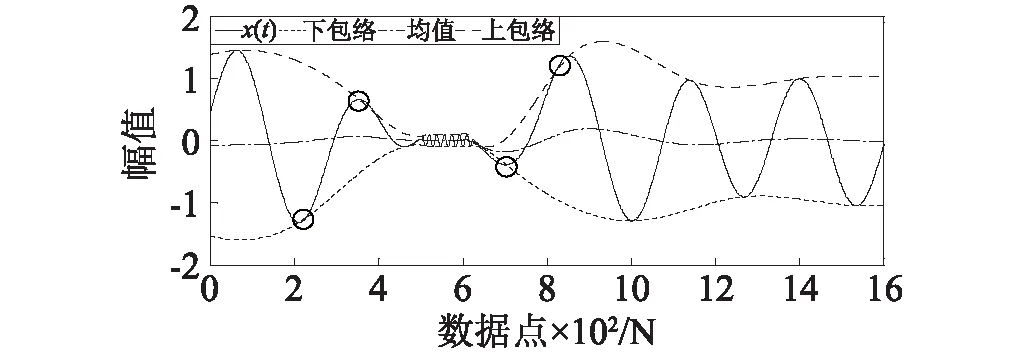
图2 含间断事件的极值包络Fig.2 Extremal envelope with intermittent events

由图2可知，间断事件造成模态混叠的原因主要是间断事件的出现使信号的时间特征尺度在局部范围内发生显著改变，造成EMD分解时因极值包络拟合“过冲”(如图2中圆圈处所示)产生较大的拟合误差，拟合误差会在后续包络拟合过程中逐步传递和扩散，使分解后的各阶IMF产生严重模态混叠。x(t)分别经EMD和CEEMD分解后获取的各阶IMF，如图3所示。

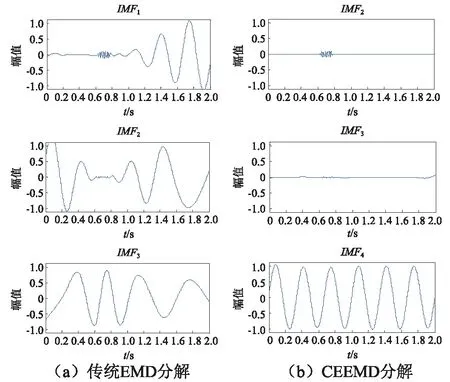
图3 模态分解比较Fig.3 Mode decomposition comparison

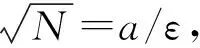
1.2 密集模态与信号调频

传统EMD算法因被分解信号各阶模态频率接近而不能将其正确分离，称此时信号中的各阶模态为密集模态，被分解信号为密集模态信号。给出信号模型

x(t)=a1cos(2πf1+φ1)+a2cos(2πf2+φ2)

(5)

为简化分析，令a1=a2=1，φ1=φ2=0，简化后进行和差化积，得

x(t)=2cos π(f1-f2)tcos π(f1+f2)t

(6)

可见信号相邻频率接近时可视作调幅信号，而调幅信号具备极值包络的均值为零和过零点数目与极值点数目相同或差一个的条件。因此，当相邻IMF频率接近时传统EMD分解会产生模态混叠。模态的EMD可分解性与相邻IMF的幅值频比和模态频比有关[20]，以信号模型为例，其EMD可分解条件为

(7)

传统的EMD分解只能将同时满足模态频比和幅值频比条件的信号正确分解，本文将式(7)作为密集模态的定量判别准则。

信号调频可以间接实现密集模态分离，避免因密集模态相互作用造成的模态混叠。其核心思想是：通过信号调频使相邻模态频率同时减去适当的调频频率，使调频后的信号变为非密集模态信号；其后，对调频后的信号进行模态分解获得imf；最后，对imf进行调频逆变换得到真实的IMF。称该模态分解方法为FM-EMD，以简化后的密集模态信号模型x(t)为例介绍FM-EMD的分解过程，可通过以下步骤实现[21-22]:

步骤1对密集模态信号模型x(t)实行Hilbert变换得到与之对应的唯一虚部iH[x(t)]，构造与x(t)对应的解析信号X(t)。

X(t)=x(t)+iH[x(t)]

(8a)

(8b)

把式(8b)代入式(8a)，可得

X(t)=x(t)+iH[x(t)]=
cos(2πf1t)+cos(2πf2t)+i(sin(2πf1t)+sin(2πf2t))=
exp(iω1t)+exp(iω2t)

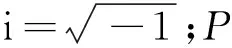
步骤2选择和合适的调频频率ω0，对X(t)实行调频变换，即将X(t)乘以e-iω0t得到调频后的解析信号Z(t)。

Z(t)=Zr(t)+iZj(t)=
X(t)×exp(-iω0t)=
exp[i(ω1-ω0)t]+exp[i(ω2-ω0)t]

(9)

步骤3对Z(t)的实部Zr(t)和虚部Zj(t)分别进行经验模态分解

(10a)

(10b)

式中：Crk,Cjk分别为Zr(t)和Zj分解出的IMF分量；rnr和rnj为常数或趋势项。

步骤4将式(10)代入式(9)后，Z(t)可表示为

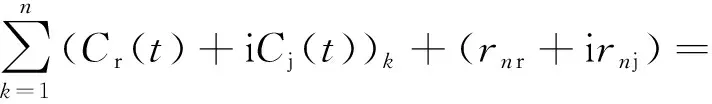
(11)

式中：Ck(t),Rn为Z(t)的实部和虚部分解后的叠加，且均为复数。当实部和虚部分解出的IMF分量数量不一致时，为避免能量泄露可以补充零向量与多出的低频IMF分量进行叠加。

步骤5将Z(t)乘以eiω0t进行调频逆变换得到X(t)，并取其实部得到原始信号x(t)

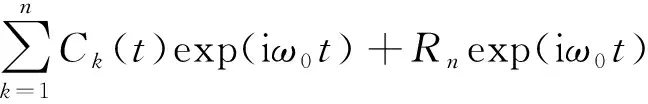
(12)

x(t)可表示为

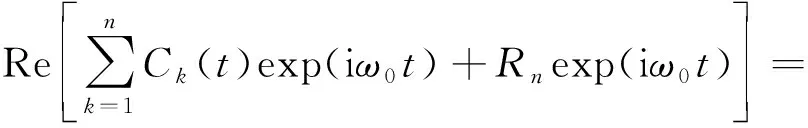
(13)

信号调频过程中，调频频率的选择至关重要。主要考虑使调频频率满足模态频比条件f0>2f2-f1，幅值频比要求可以在确定调频频率范围后通过调试满足。根据密集模态信号定义可知2f2-f1>0，有f0>2f2-f1>0成立，因此一定存在某个正频频率满足模态频比要求。对于频率未知的实测信号，选取调频频率时首先通过原始信号的傅里叶变换初步估计信号的频率值，其后以f0>2f2-f1>0为依据调试选取合适的调频频率。

1.3 抑制模态混叠的FM-CEEMD分解

实测信号通常既包含间断事件又包含密集模态，单凭信号调频或CEEMD分解往往不能有效抑制模态混叠。因此，将信号调频与CEEMD分解进行有机结合得到抑制模态混叠的组合办法，称其为FM-CEEMD模态分解方法，具体分解步骤与FM-EMD相同。

构造信号x(t)为两个单频正弦密集模态信号的叠加，并向其添加两段高频小幅值间断信号模拟间断事件的作用。

x(t)=x1(t)+x2(t)+x3(t1)+x4(t2)

(14)

x1(t)=sin(2πt×3)

(15)

x2(t)=sin(2πt×2)

(16)

式中：x3(t1)和x4(t2)为频率为45 Hz，幅值为0.1的高频小幅值间断信。

分别采用CEEMD，FM+EMD和FM+CEEMD方法对x(t)进行分解，其中调频频率为1.48 Hz，噪声标准偏差倍数设为0.1，加噪次数设为100，各阶IMF及其频谱如图4所示。

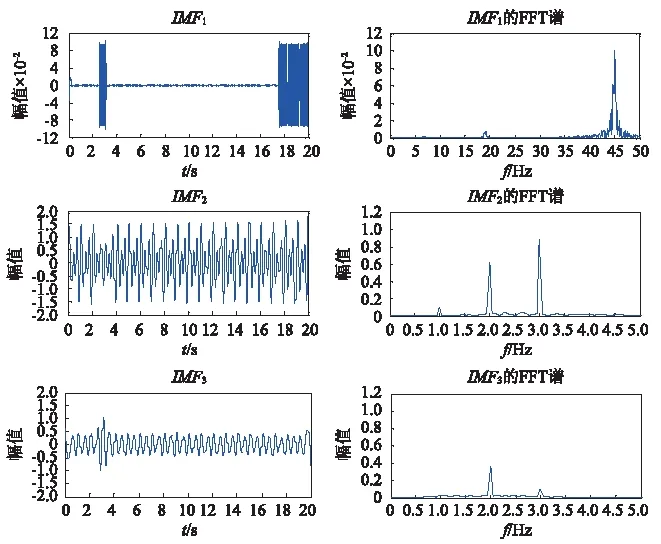
(a)CEEMD分解

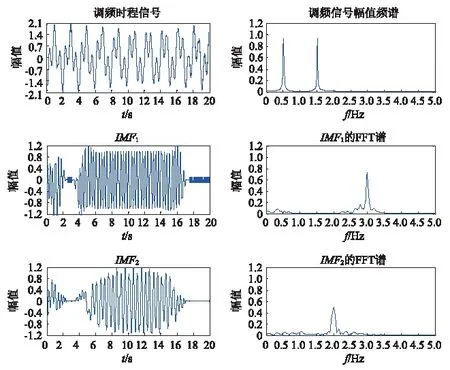
(b)FM+EMD分解

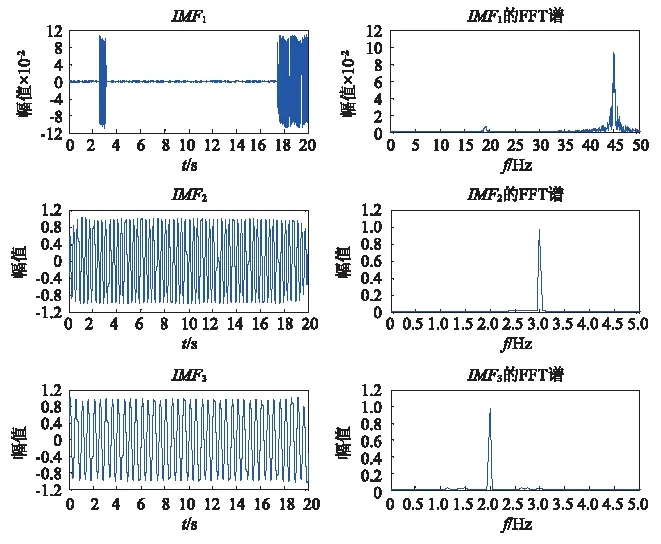
(c)FM-CEEMD分解

分析图4可知，CEEMD能将间断信号准确分解到IMF1中，但对密集模态造成的模态混叠作用不大，IMF2包含了两阶模态信息。FM-EMD能准确分离密集模态，但对间断信号造成的模态混叠作用不大，IMF1中既包含间断信号也包含频率为3 Hz的信号。FM-CEEMD模态分解方法，既有效避免了间断信号对模态分解的影响又抑制了密集模态相互作用造成的模态混叠，分解出的各阶IMF具有实际物理意义。为定量评价FM-CEEMD模态分解方法的性能，引入模态分解均方误差NMSE。

(17)

式中：fi(t)为与第i阶imf对应的值为信号分量。

三种模态分解方法对应的各阶IMF分解均方误差NMSE，如表1所示。可见FM-CEEMD分解得到的各阶IMF的均方误差更小，更接近真实的信号分量。

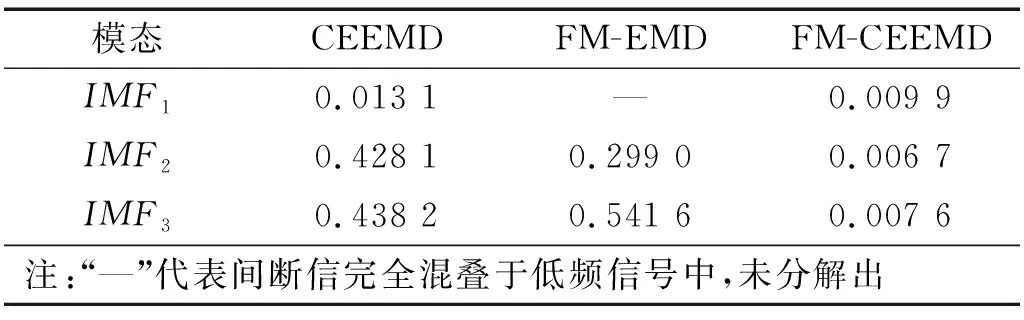
表1 标准均方误差比较

2 抑制模态混叠的HHT结构模态参数识别方法

2.1 HHT结构模态参数识别原理

振动信号经EMD分解得到表征实际物理过程的IMF，并对IMF进行HT分析得到结构动力参数。单自由度线性阻尼结构体系，承受脉冲荷载后的振动时程曲线为

y(t)=A0e-ξω0tcos(ωdt+φ0)

(18)

式中：ωd,ω0和ξ分别为有阻尼固有频率、固有频率和阻尼比；A0为冲击荷载作用下的初始位移，其与冲击荷载强度和结构质量、频率特性有关。对y(t)进行HT变换，并构造与其唯一对应的解析信号。

(19)

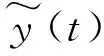
A(t)=A0e-ξω0t

(20)

θ(t)=ωdt+φ0

(21)

对A(t)求对数，θ(t)求微分，得

lnA(t)=-ξω0t+lnA0

(22)

(23)

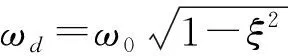
图5 传统HHT参数识别流程Fig.5 Parameter identification flow chart of traditional HHT

2.2 抑制模态混叠的HHT识别法

针对传统HHT结构模态参数识别的模态混叠问题，用带通滤波和信号调频控制CEEMD分解过程，避免因间断事件和密集模态造成的模态混叠。将改进后的方法称为抑制模态混叠的HHT结构模态参数识别法。具体实施步骤如下：

步骤1绘制自由衰减响应的归一化功率谱图，根据功率谱图选择合适频带对信号进行带通滤波，得到不同频带分量；

步骤2获得各频带分量的归一化功率谱图，判断频带内是否含有不同模态信息；

步骤3若只含单阶模态信息，则直接对频带分量进行CEEMD分解，并选择与原始信号或相关函数(NExT法得到)偏差系数小的模态作为特征IMF；若含多阶模态，则用FM-CEEMD将易产生模态混叠的不同模态分解出来；

步骤4对特征IMF进行RDT处理，并用HT法识别模态参数。

偏差系数SD，计算公式为

(24)

式中：imfi(t)为第i阶IMF分量;s(t)为原始信号或相关函数。改进的HHT结构参数识别流程，如图6所示。

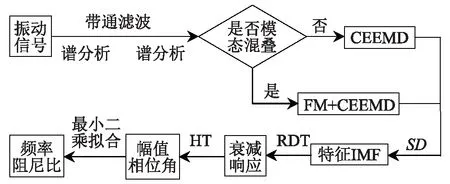
图6 改进HHT参数识别流程Fig.6 Parameter identification flow chart of improved HHT

3 仿真与实例验证

3.1 仿真试验

三自由度密集模态系统，如图7所示。刚度k1,k2,k3,k4分别为30 kN/m,15 kN/m,15 kN/m,30 kN/m；质量m1,m2,m3均为1 000 kg；阻尼c1,c2,c3,c4分别为120 N·s/m, 45 N·s/m， 45 N·s/m， 120 N·s/m。

图7 密集模态系统Fig.7 Dense mode system

为模拟实测信号中的噪声干扰，向冲击荷载作用下的振动曲线中加入幅值为1的高斯噪声，振动幅值衰减曲线如图8所示。

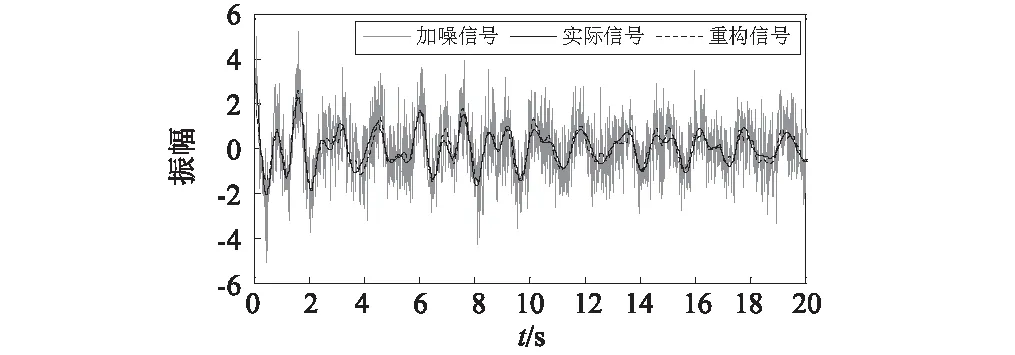
图8 振动幅值-时程曲线Fig.8 Vibration amplitude-time curves

自相关去除加噪信号的噪声干扰，保留确定性周期信号，去噪重构信号如图8所示。经计算，加噪信号信噪比为-5.4 dB，重构信号信噪比为7.65 dB，互相关系数为0.975 2。由去噪重构信号的归一化功率谱密度可知，信号在1.3 Hz，1.18 Hz和0.67 Hz存在明显峰值，分别用0～1 Hz和1～2 Hz对去噪重构信号进行带通滤波得到信号分量x1,x2，分量x2的归一化功率谱密度含有两个峰值判断其存在模态混叠。

为了对比分析FM-EMD和FM-CEEMD对含噪密集模态信号的分解效果，选用1.08 Hz的调频频率对分量x2分别进行FM-EMD和FM-CEEMD分解，将混叠模态分解出来。对各特征IMF进行RDT处理，并用HT法识别模态参数。其中，FM-CEEMD分解后识别出的第2阶模态信息和FM-EMD分解后识别出的第3阶模态信息，如图9所示。

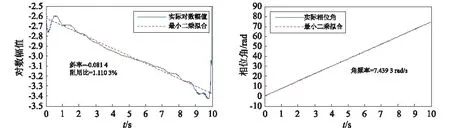
(a)FM-CEEMD分解后识别出的第2阶模态

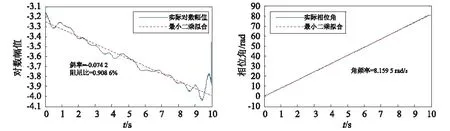
(b)FM-EMD分解后识别出的第3阶模态

运用ITD法、传统HHT法、HHT法(FM-EMD)和改进HHT法(FM-CEEMD)对密集模态系统进行模态参数识别，结果如表2所示。

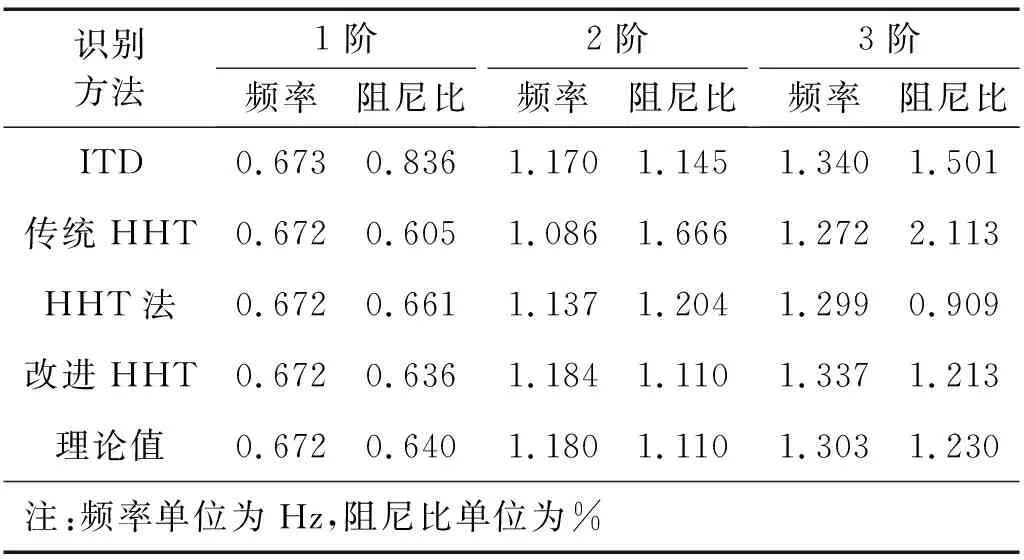
表2 结构动力参数识别结果

由图9和表2可知，信号经过FM-EMD和FM-CEEMD分解后再进行HT模态参数识别均能获取较精确的频率信息，但FM-EMD分解后的阻尼比识别精度较低。阻尼比识别精度的高低取决于HT分析中对振动对数幅值曲线拟合的好坏，本质归结于不同分解方法获取的自由衰减响应质量的好坏。两种模态分解方法处理的对象虽然为去噪后的信号，但此时信号中的噪声不可能完全去除。因此，FM-CEEMD分解能抑制噪声和脉冲干扰，更准确的提取模态自由衰减响应，进而阻尼比的识别精度更高。

由表2还可知，传统HHT法虽未因模态混叠造成模态信息丢失，但2阶、3阶的频率和阻尼比识别结果均与理论值差距较大；改进HHT法和ITD法均能较精确识别模态频率，但ITD法的阻尼比识别结果较差；改进HHT法在频率和阻尼比识别方面均表现优异，在四种模态识别方法中具有最高的参数识别精度。

3.2 拱坝模态参数识别

高双曲拱坝是典型的密频结构，采用本文中提出的抑制模态混叠的HHT法识别坝体振动的模态信息。某混凝土双曲拱坝，汛期沿坝顶拱圈顺水流方向布设9支频响为0.35～200 Hz，灵敏度为8 mV/μm的水平振动位移传感器，观测泄流激励下坝体的振动响应，测点布置如图10所示。

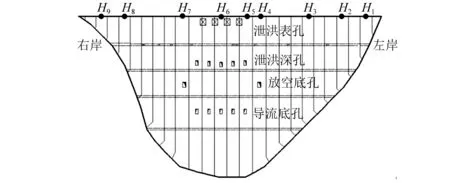
图10 测点布置Fig.10 Layout of measuring points

泄流激励下拱坝振动幅值较小，有用信号容易淹没于环境噪声，且观测期间存在坝肩施工干扰，因此毗邻坝肩的H1和H9测点不予分析。选择振动幅值较大的坝顶拱圈中部H5作为分析测点，振动幅值较小的右坝肩H8作为参考测点，两测点在表孔全开工况下的振动幅值时程曲线，如图11所示。

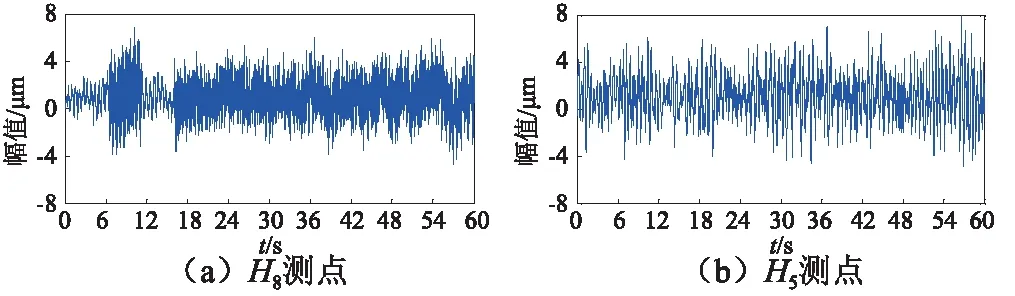
图11 振动幅值-时程曲线Fig.11 Vibration amplitude-time curves

由图11可知，两测点的振动幅值时程曲线均出现“零漂”，采用多项式最小二乘法消除趋势项，并采用滑动平均法消除信号中的毛刺。信号预处理后，H5以小振幅的H8作参考点，通过自然激励技术(Natural Excitation Technique，NExT)求得的相关函数及其归一化功率谱密度，如图12所示。

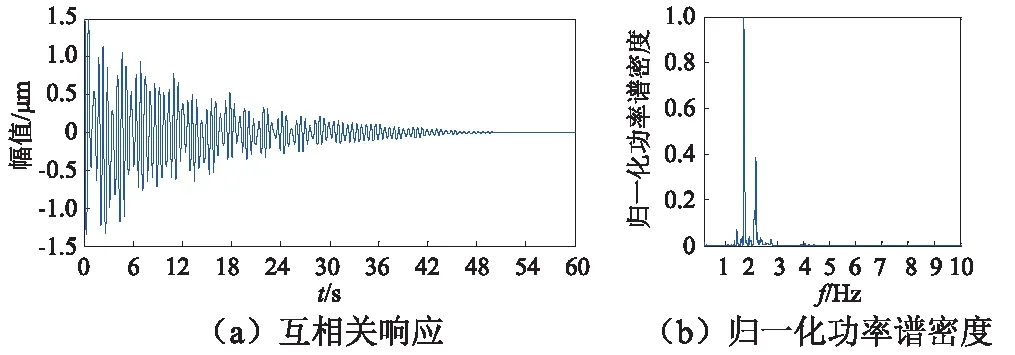
图12 互相关响应及其功率谱密度Fig.12 Cross-correlation response and power spectral density

互相关响应的归一化功率谱密度在1.4 Hz, 1.7 Hz, 2.7 Hz和4.2 Hz附近存在较明显的峰值，因此用0.9～1.9 Hz, 1.9～2.9 Hz, 2.9～3.9 Hz和3.9～4.9 Hz的频带对互相关响应进行带通滤波，得到x1,x2,x3和x44个滤波分量，并作各分量的归一化功率谱密度，如图13所示。

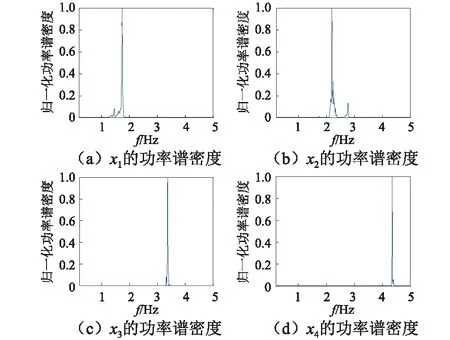
图13 滤波分量的归一化功率谱密度Fig.13 Normalized power spectral density of filter component

由滤波分量的归一化功率谱密度可知，x3和x4中只含单阶模态信息，直接对其进行CEEMD分解，并选择与相关函数偏差系数小的模态作为特征IMF；x1和x2的功率谱密度含有两个峰值，判断其含有两阶模态信息，使用FM-CEEMD分解获取不同模态信息。以x1为例，其在1.44 Hz和1.74 Hz处存在明显峰值，选用

1.30 Hz的调频频率对x1进行FM-CEEMD分解，选择与x1偏差系数小的两阶模态作为特征IMF。x1经FM-CEEMD分解后得到的两阶特征IMF及其功率谱密度，如图14所示。图14(b)和图14(d)分别为IMF1和IMF2的归一化功率谱密度，两阶IMF功率谱密度中只含有单个峰值，表明调频处理有效解决了模态分解过程中密频造成的模态混叠。

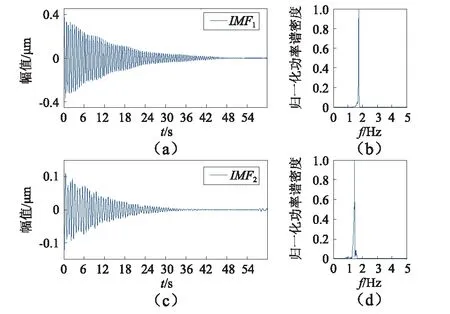
图14 FM-CEEMD模态分解结果Fig.14 Modal decomposition results by FM-CEEMD

对各特征IMF进行RDT处理，并用HT法识别模态参数，H5测点的第2阶模态参数识别结果，如图15所示。同理可得其它模态参数。

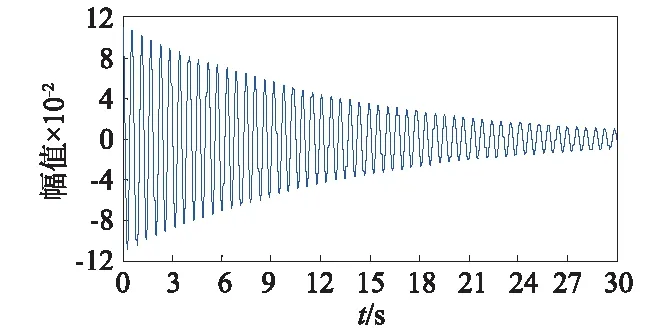
(a)自由衰减响应

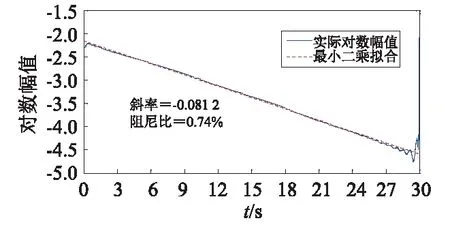
(b)对数幅值拟合

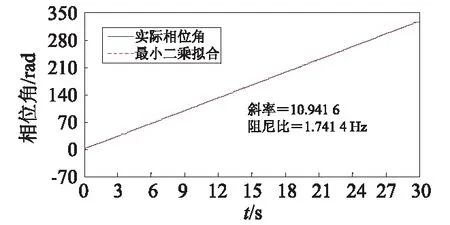
(c)相位角拟合

图15 第2阶模态参数识别结果

Fig.15 Parameter identification results of second modal

运用ITD法、传统HHT法和抑制模态混叠的改进HHT法分别对H5测点进行模态参数识别，结果如表3所示。

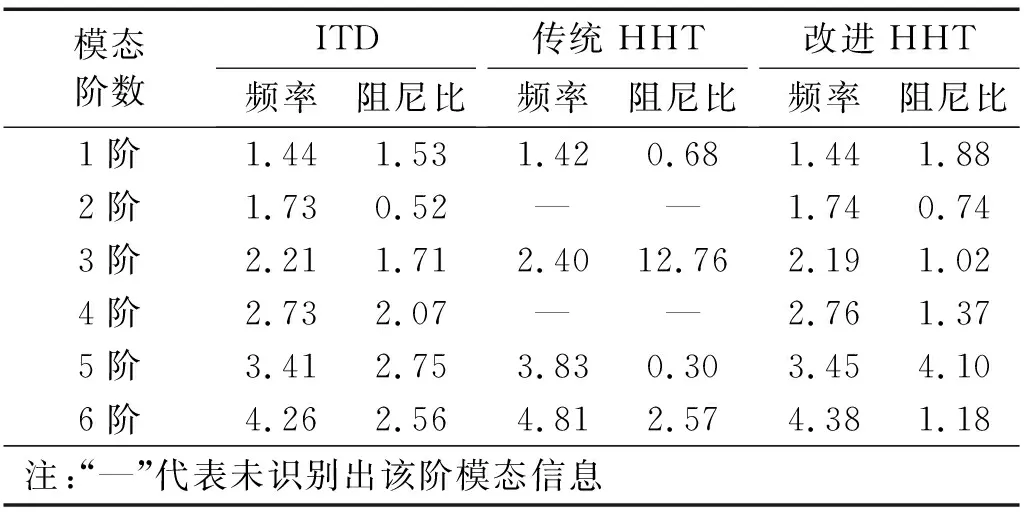
表3 模态参数识别结果

为检验改进HHT法模态参数识别效果，根据功率谱密度对拱坝典型泄流工况下的主频和3阶频率进行统计，发现主频位于1.43～1. 47Hz，3阶频率位于2.17～2.21 Hz。改进HHT法识别的模态频率均位于统计频率范围内，且与ITD法识别结果接近。传统HHT法未能识别2阶和4阶模态信息，且参数识别结果与频率统计结果相差较大。相比传统HHT法，改进后的HHT法能有效抑制因噪声干扰和密集模态造成的模态混叠，并有效提高模态参数识别精度。