基于优化粒子群的货物装箱管理方案

胥珠峰

（河海大学商学院 南京 210098）

1 引言

货物装箱管理随着物流标准的不断推行，使得问题变得尤为凸显［1］。无论是通过装载方案节约单位货物的运输成本，还是提高装载效率提升综合能力，经典的组合优化问题随着装箱规模的增加使计算的复杂性持续提升［2］。利用数学优化算法解决货物装箱问题的能力是有限的，例如启发式算法［3］、遗传算法［4］和模拟退火算法［5］等。而尽管粒子群算法优点明显，但也和其他全局优化算法一样，有易早熟，易陷入局部最优的缺点，避免算法早熟能够有效提高算法的收敛精度［6］。本文在简化粒子群算法的基础上引入小生境技术与混合蛙跳算法，将粒子群按照适应度值大小进行分组，结合混合蛙跳算法进行更新迭代，采用小生境技术改进策略，将初始种群按照欧式几何距离（装箱序列差异）分成多个子群（小生境），各子群单独进化，周期性地取出各子群最优粒子组成新种群应用混合蛙跳算法进行更新，进一步提升种群多样性与全局寻优能力。通过改变种群的拓扑结构，引入多种群的概念，改进算法的更新公式，通过该过程弥补其易早熟的缺点，提高其全局寻优能力与收敛精度。

2 模型建立

2.1 目标函数

建立目标函数之前，为方便研究，本文还需要以下假设：1）货物正交装载；2）货物只允许水平旋转；3）集装箱和货物均能无限载重；4）货物之间不存在优先级。假设箱体的长、宽和高分别为L、W和 H ，待装载货物的集合为 C={C1。C2。...。Cn}，货物Ci的长、宽、高分别为li、wi和hi。若货物Ci装入集装箱中表示为ai=1；货物Ci未装入集装箱中表示为ai=0，需要达到的要求为满足给定约束条件下的最大体积装载率，以提高集装箱的空间利用率获得最佳效益。目标函数如：

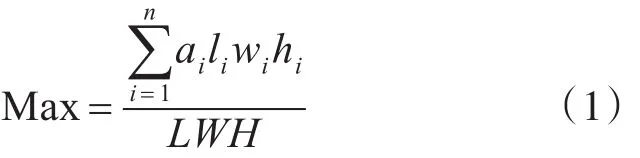
2.2 装载策略

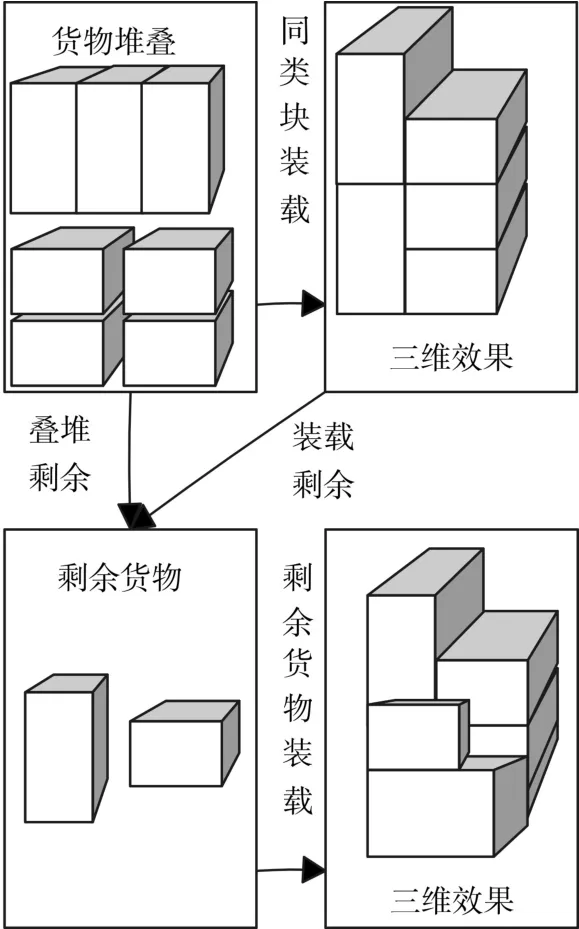
图1 装载策略

同类块的堆叠数量为在给定箱体高度下的最大数量，堆叠剩余后的货物连同按照当前装载方案无法装入箱体的同类块构成当前装载方案下的剩余货物。将同类块看作矩形块应用二维启发式排样算法进行装载［7］；已装入集装箱的同类块与箱体顶部之间可能存在可放下若干剩余货物的剩余空间，该空间进行适当合并后亦可能装入较大的剩余箱子或产生更优的装载组合，从而提升集装箱的空间利用率。剩余空间与剩余货物的种类较少，装载搭配有限，故采用规划类排样算法直接求取最优组合［8］。装载策略示意如图1所示。

2.3 同类块装载

采用剩余矩形算法实现同类块的装载，该算法是一种动态局部寻优算法。首先在母板的指定位置放下第1个矩形件，按照面积占比最大的原则将矩形件依次放入空白间隙中，排入N个矩形件会产生N+1个空白间隙，每次装载后进行更新，直到排入所有矩形块或没有适当的空白间隙为止。假设母板左下角与右上角的位置坐标分别为(X0。Y0)和(X1。Y1)。所有矩形件的下料点为空白间隙的左下角。当排入长宽分别为l1和w1的矩形件时，产生 了 两 组 空 白 间 隙 (X0+l1。Y0) 、(X1。Y0+w1) 、[(X0。Y0+w1)。(X1。Y1)] 或 [(X0+l1。Y0)。(X1。Y1)] 、[(X0。Y0+w1)。(X1+l1。Y1)]；放入长宽分别为 l2和 w1的矩形件后，更新后产生的3个空白间隙有多种组合，举例其中一种组合为 [(X0+l1。Y0)。(X1。Y1+w1)]、[(X0+l2。Y0+w1)。(X1。Y1)] 和 [(X0。Y0+w1+w2)。(X0+l2。Y1)]，排样示意过程如图2所示。

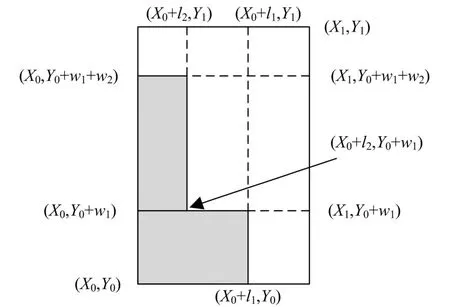
图2 排样示意过程

采用连分数算法实现剩余货物的装载［9］，在能够实现方案最优的前提下该算法时间效率最高。装载过程遵循以下规则：

1）剩余空间按货类合并为长方体型剩余空间，剩余货物按货类进行分组。

2）剩余货物按组装入当前未装载的最大合并空间，取其中空间利用率最大的装载方案进行装载。

3 粒子群算法

3.1 简化粒子群算法

经典粒子群算法中粒子包含位置与速度两个基本属性［10］，粒子的更新通过改变粒子的速度间接影响粒子位置来实现。通过分析经典粒子群算法的运行机制，提出进化过程与粒子速度无关的定理，剔除了经典粒子群算法中的速度项，仅由粒子位置控制进化过程，避免了由粒子速度项引起的粒子发散而导致后期收敛变慢和精度低的问题［11］。简化后的更新公式如：

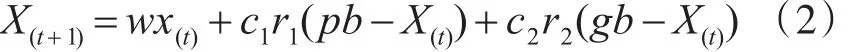
其中，w表示收缩因子；t代表当前的演化代数，t+1代表当前演化代数的下一代；X(t)和X(t+1)分别表示粒子在第t和t+1；pb和gb分别表示个体的历史最优位置和群体的历史最优位置；c1和c2分别表示个体学习因子和全局学习因子；r1和r2均为0～1之间的随机数。

3.2 编码方式

1）粒 子 位 置 ，一 个 装 载 序 列 X=(r1N1。r2N2。…。rnNn)就代表了一个粒子的位置，即装箱方案的一个解。其中Ni和ri分别代表货块的类和旋转因子，其取值为1或-1，若货块正常装载表示为ri=1，货块水平旋转90°装载表示为ri=-1。

2）置换子，设粒子k的位置为 Xk，则置换子(riik。rjjk)代表交换 Xk中序号为ik和 jk的货块位置，并继承置换子中的旋转因子。即

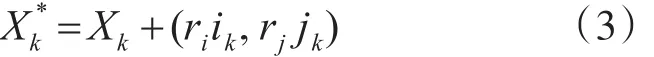
3.3 基本操作

1）位置-间距：将置换序列按顺序依次作用在粒子位置上，生成新的粒子位置；

2）位置-位置：计算两个粒子的位置间距，得到粒子间距（置换序列）；

3）间距-间距：两个粒子间距（置换序列）按照顺序组合成一个新的置换序列；

4）实数-间距：实数与置换序列中置换子的数量相乘，向前取整得到整数，取出前个置换子构成新的置换序列。

举例某粒子的更新过程如图3所示。

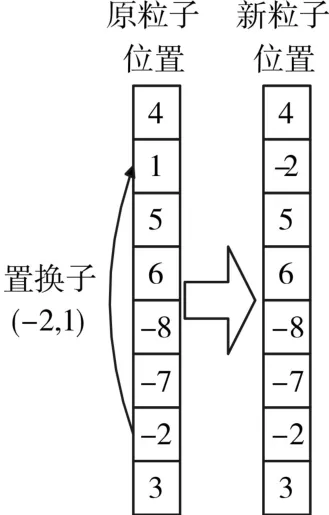
图3 粒子更新

4 优化粒子群算法

4.1 局部搜索优化

小生境技术（NT）起源于遗传算法，该方法基于群体的随机优化算法形成物种［12］，利用其保持种群多样性的特点弥补粒子群算法易陷入局部最优的缺陷，同时提升了种群的局部搜索能力［13］。应用过程为：计算每个粒子的欧式几何距离（装箱序列差异），将粒子按从小到大的顺序依次取出，将初始种群均分为P个子群，各子群单独进化。因此需要增加新变量：子群的历史最优位置g*b，更新公式变化如：

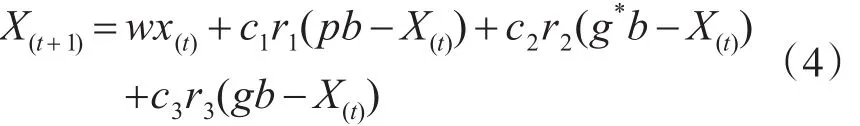
其中，c2和c3分别表示子群学习因子和全局学习因子；r3表示0～1之间的随机数。

4.2 群体优化

为了实现各子群之间的信息交流，提升各子群最优解的质量，采用混合蛙跳算法（SFLA）实现优化过程［14］。该算法是一种群体进化算法，先将种群划分为若干个子群进行局部搜索，再全局混合以达到全局交流的目的，有效提升种群的全局寻优能力［15］。应用过程为：达到迭代周期后，取出各子群最优解组成蛙群，按照适应度值依跨度均分为M个子群，在每个子群中，记录下当次迭代适应度最好的个体Xb和适应度最差的个体Xw，并计算两者之间的间距dj，同时记录整个蛙群的最优个体Xg。在每次迭代时，对子群中适应度最差的个体Xw进行更新，如下所示：

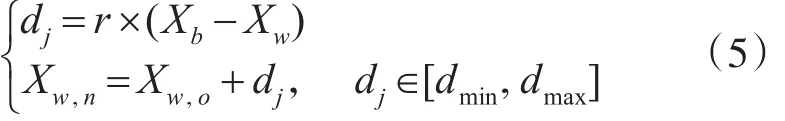
其中，r表示0～1之间的随机数，Xw。n和 Xw。o分别表示子群最差个体的新解与旧解；dmin和dmax分别表示间距的最小值与最大值。更新过后，若有改进，则用新解替代旧解；若没有改进，则将Xg替换Xb进行更新；若仍无改进，则随机产生一个解替代旧解。

4.3 算法流程

改进粒子群优化算法具体流程如下：

步骤1：初始化粒子群的初始位置，设置相关参数；

步骤2：根据粒子的欧式几何距离（序列差异程度）将粒子群分成P组，每组Q个；

步骤3：使用装载算法进行装载，计算粒子适应度值F；

步骤4：更新粒子的个体历史最优位置 pb、子群历史最优位置g*b以及全局历史最优位置gb；

步骤5：按照式（4）进行更新。是否达到迭代周期，若是，则跳到步骤6；否则跳到步骤9；

步骤6：取出各子群最优位置g*b组成蛙群，按照适应度值进行排序分组，分为M组，每组N个；

步骤7：使用装载算法进行装载，计算粒子适应度值F，更新子群最优粒子 Xb，最差粒子 Xw以及全局最优粒子Xg；

步骤8：按照式（5）进行更新子群最差粒子的位置。是否达到迭代次数，若是，则跳到步骤4；否则跳到步骤7；

步骤9：是否达到终止条件，若是，则执行结束；否则跳到步骤3继续执行。

5 仿真分析

5.1 参数设置

根据本文的目标函数及约束条件，选择L&N经典算例中的L&N01与L&N05进行测试。两组数据均是典型的弱异构类装箱问题，且货物不能被集装箱全部装下，使用Matlab实现算法。经过调试，确定粒子群规模为30，迭代100次；初始种群均分为6个子群（小生境）。每迭代10次进入混合蛙跳算法更新过程，蛙群均分为2组，更新5次退出循环：w=1，ci=1，i=1。2。3。

5.2 实验结果

每个算例独立循环10次，记录运行结果，分别取其中最优解进行统计：两算例均有200个货物，其中L&N01装入172个货物，空间利用率为92.82%；L&N05装入139个货物，空间利用率为93.36%。具体装载信息如表1所示。

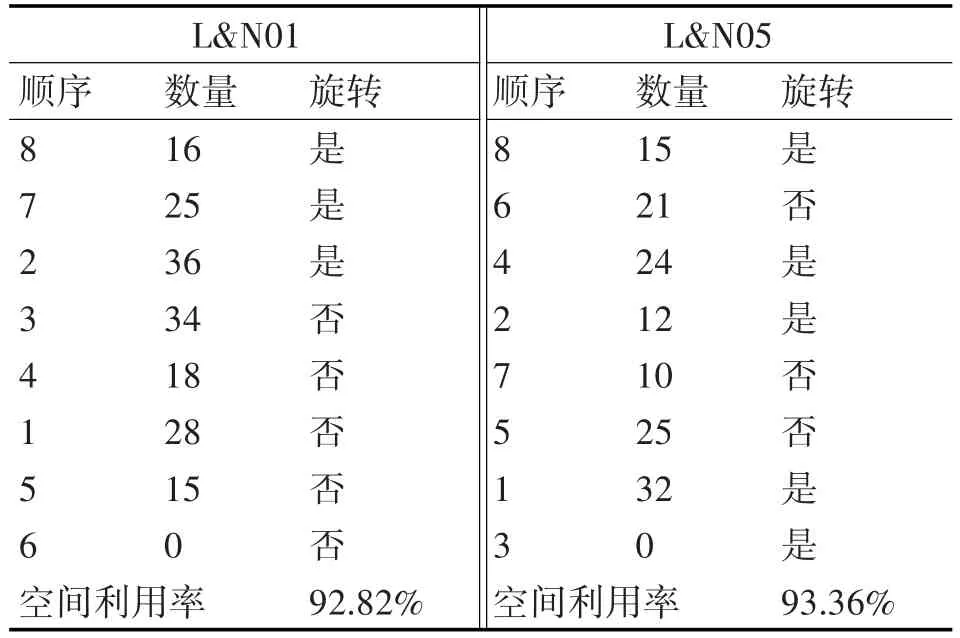
表1 实验结果

5.3 对比分析

应用经典粒子群算法与改进算法在同一条件下求解，分别绘制最优解对应的迭代过程对比图，L&N01如图4所示、L&N05如图5所示。

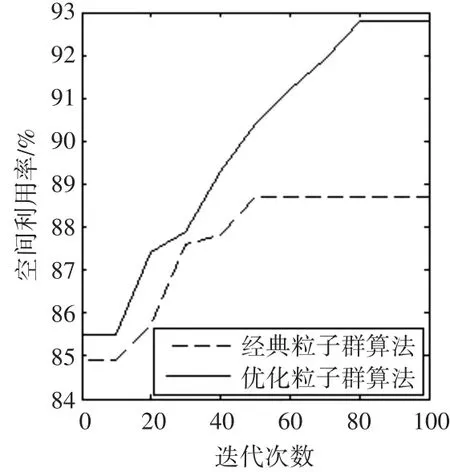
图4 L&N01算法迭代过程对比

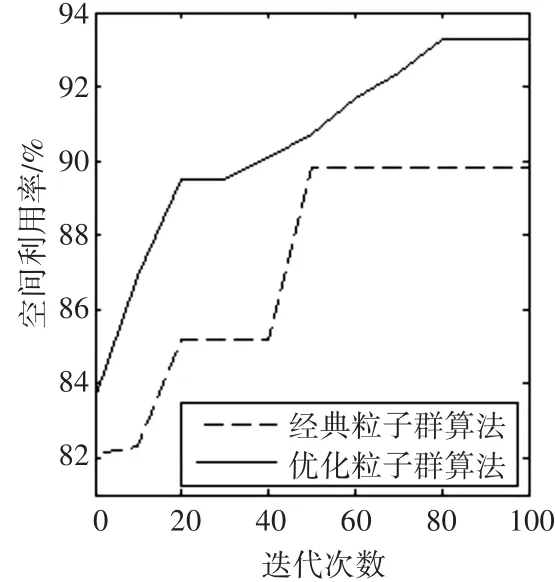
图5 L&N05算法迭代过程对比

从图4和图5中看出：经典粒子群算法在迭代前期便陷入了局部最优直到迭代结束，改进算法的解在迭代后期仍能不断提升；在整个迭代过程中改进算法始终显著优于经典粒子群算法的解。由对比可知：改进算法能够使粒子跳出局部最优，提升全局寻优能力，显著提高求解效率。以L&N算例验证其求解算法，将这些算法与改进算法进行比较，对比结果如表2所示。

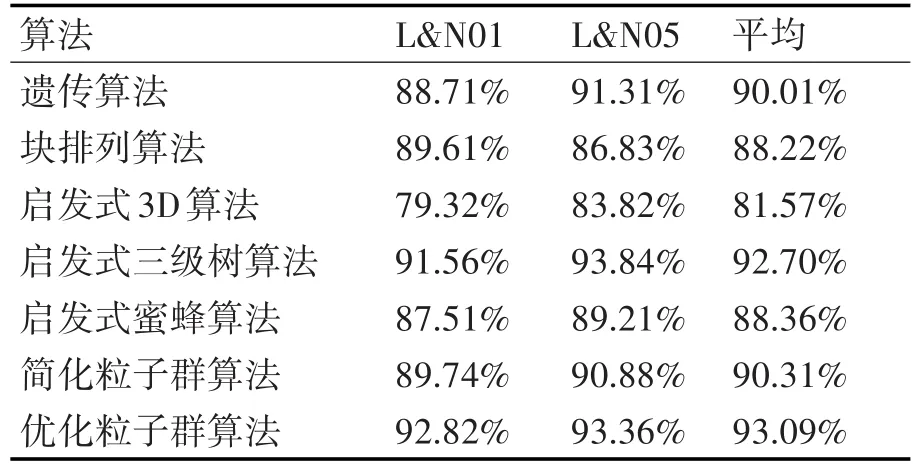
表2 结果对比

从表2可以看出：本研究提出的优化粒子群算法对L&N01的求解质量高于其他算法，较其中最优解提升1.26%；优化粒子群算法对L&N05的求解质量略低于其他的算法，较其中最优解低0.48%；综合来看，本研究提出的优化粒子群算法的平均求解质量达到93.09%，优于其他算法的结果，较其中最优解提升0.39%；与同采用粒子群算法（简化粒子群算法）的方式比较，优化粒子群算法的平均求解质量较前者高2.78%。算例对比结果验证了优化粒子群算法的有效性与优越性。

6 结语

优化粒子群算法作为一种新型的智能算法，研究如何将该算法应用于求解实际问题具有很大的实用价值。本文将优化粒子群算法应用于货物装箱管理问题，并针对其搜索精度不高、容易陷入局部最优解的缺点引入小生境技术与混合蛙跳算法进行弥补，提出一种优化粒子群算法。在装箱策略上，为简化装载过程采用同类块的思想，应用排样算法实现装载。对比结果表明优化后的算法能够跳出局部最优解，具备较强的全局寻优能力，有效提升单箱弱异构货物装箱的空间利用率，具备较强的实践价值。