求解超定病态线性方程组的一种正则化迭代算法

李鹏飞 佟喜峰 李鹏举

（1.东北石油大学计算机与信息技术学院 大庆 163318）（2.东北石油大学地球科学学院 大庆 163318）

1 引言

在地球物理反演问题中，大多数建立的数学模型都是超定病态线性方程组［1］，此时方程组为矛盾方程组，往往是无解的。即便方程有精确解，由于方程组的系数矩阵是病态的，直接解法和迭代解法等求解方法，所得到的数值解是不稳定的［2］，往往因误差太大而失去意义。

目前，针对病态线性方程组的求解方法可以分为如下几类。截断奇异值分解法［3～5］，正则化方法［6～7］，条件预优法［8～9］，进化一类的算法，比如遗传算法求解［10～11］。截断奇异值分解法具有克服病态能力强，不放大误差的特点，但是截断参数确定较困难。正则化一类的方法是用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解，其正则参数的选取对问题解的性态起关键作用。参数值太小对系数矩阵的条件数改善不明显，近似解的误差很大。而参数值太大，新问题的解稳定了，但是与原问题相差太大。可以用先验原则和后验原则来确定正则参数，但不幸的是，这两种方式确定正则参数都比较麻烦。条件预优法通过构造预优矩阵左乘原方程组，来降低系数矩阵的条件数，这样也是用一个新问题的解去近似原问题的解。但是这种方法寻找预优矩阵比较复杂。遗传算法的优点是全局优化，在多数情况下，遗传算子的参数设定需要根据解的分布情况做动态改变，否则算法容易早熟而收敛到局部最优解。

受迭代Tikhonov正则化思想启发，本文设计一种简单的正则化迭代算法，来求解超定病态线性方程组。

2 正则化迭代算法设计

设有如下形式的超定线性方程组：

其中：A∈RM×N。x∈RN。b∈RM。M＞N 用 AT左乘式（1），得到如下形式正则方程组：

其中：ATA∈RN×N为N阶实对称方阵。如果矩阵A为病态矩阵，此时ATA的病态性会加剧。基于Tik⁃honov正则化的思想，将式（2）系数矩阵 ATA的主对角线上元素叠加一个正则参数α，以此来降低ATA的条件数。同时为了保证与式（2）同解，可构建如下公式：

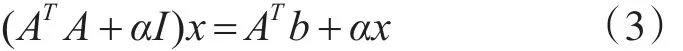
其中：α为正则系数，I为与ATA同阶的单位阵。由于式（3）等式左右两端分别含有解向量x，在式（3）两端分别乘(ATA+αI)-1，则可以构成一个一般迭代式（4）：

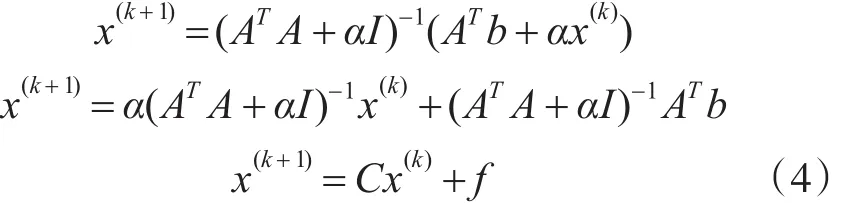
其中：K=ATA。C=α(K+αI)-1。f=(K+αI)-1ATb

要想确定式（4）对应算法是否有效必须满足两个条件，一是K+αI是否可逆，二是迭代矩阵c是否收敛。下面通过对正则参数α取值范围进行判定，进而回答式（4）对应算法何时有效。

3 正则参数取值范围判定

结论1：有实方阵K，如果K的特征值为λ，则矩阵K+αI的特征值为λ+α。

证明：设 λi为矩阵 K=(kij)n×n的第i个特征值为矩阵K+αI的第i个特征值，则对于矩阵K+αI有如下等式成立：

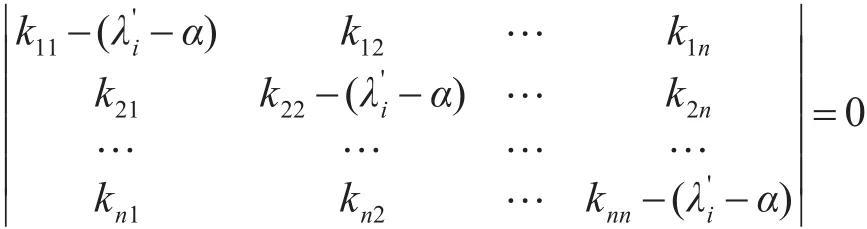
对于矩阵K则有有如下等式成立：

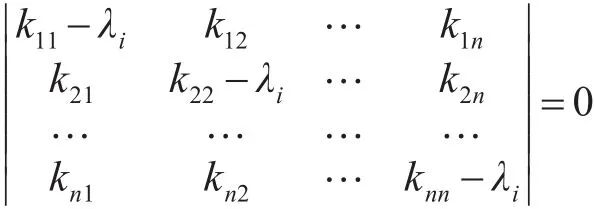
比较上式得：

结论2：如果K为对称正定方阵，当α＞0时，式（4）所构成的迭代公式必收敛。

证明：根据式（4）知其迭代矩阵为

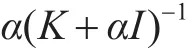
因为K为对称正定方阵，所以K的全部特征值均大于0。根据结论1和α＞0（已知）得：矩阵K+αI的全部特征值也均大于0，所以矩阵K+αI必可逆。设K的任一特征值为λ，则存在非零向量x，使得如下等式成立：

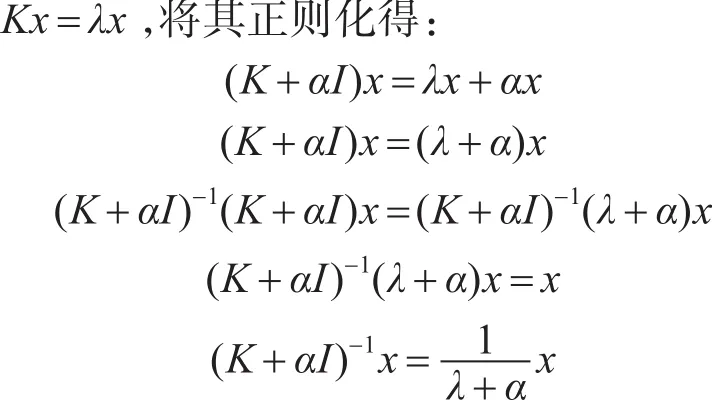
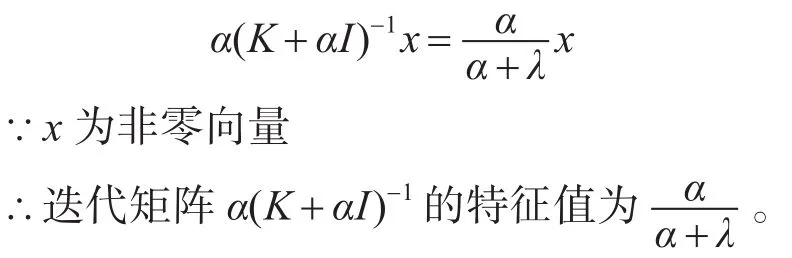
上式两端同乘以α，则：值均小于1，其谱半径也小于1，所以式（4）所构成的迭代公式必收敛。

证毕。

因此，对于对称正定矩阵选取正则参数α＞0，就可以保证矩阵 K+αI可逆，且迭代矩阵α(K+αI)-1收敛。

为了有效地降低系数矩阵的条件数，提高数值解的精度，只有α＞0的结论是不够的。对于对称阵为严重病态时，λmax＞＞λmin。此时取 α=λmax，根此时可将严重病态的系数矩阵改为良态矩阵，从而提高了数值解的精度。

4 核磁共振弛豫反演模型

根据核磁共振测井理论可知，氢原子核系统磁化强度矢量的横向分量是按指数规律衰减的，由CPMG脉冲序列测得的回波串也按指数规律衰减。储层岩石通常存在一个孔隙尺寸分布，并且常常含有多种流体成分，此时孔隙中存在多种弛豫组份，即横向弛豫时间常数（T2）不是单值，而是一个分布，称之为T2谱。由CPMG脉冲序列测量记录的自旋回波串按多指数规律衰减，即各单指数衰减的叠加。回波幅度与横向弛豫分量初始幅度之间满足式（5）关系［13］：

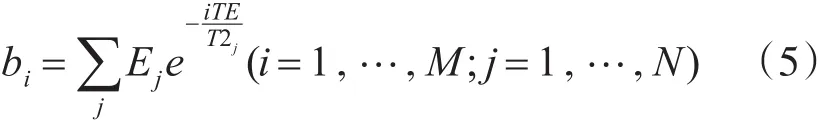
式中：bi为CPMG脉冲序列测量记录的第i个回波幅度；Ej为第j个横向弛豫分量的初始幅度（正数）；T2j为第j个横向弛豫分量衰减的时间常数；TE为CPMG脉冲序列测量记录的回波间隔；N为横向弛豫分量的个数；M为回波个数；T2谱反演就是根据预设的T2值和仪器测得的回波串数据，求解出Ei，使其满足式（5）。其实质是求解M个方程，N个未知数的线性方程组。

5 有噪声理论数据反演

考虑如下核磁共振测井T2谱反演模型：

其中：所有算法均在Matlab上实现。

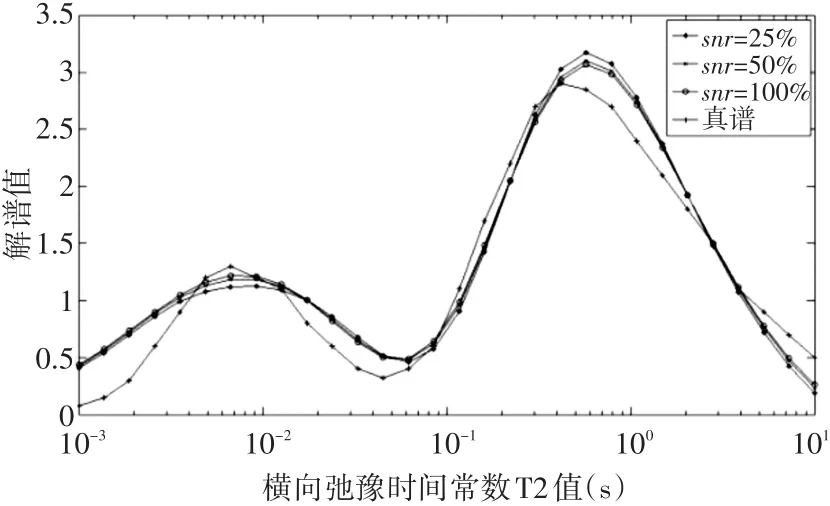
图1 不同信噪比正则化迭代算法解谱对比图

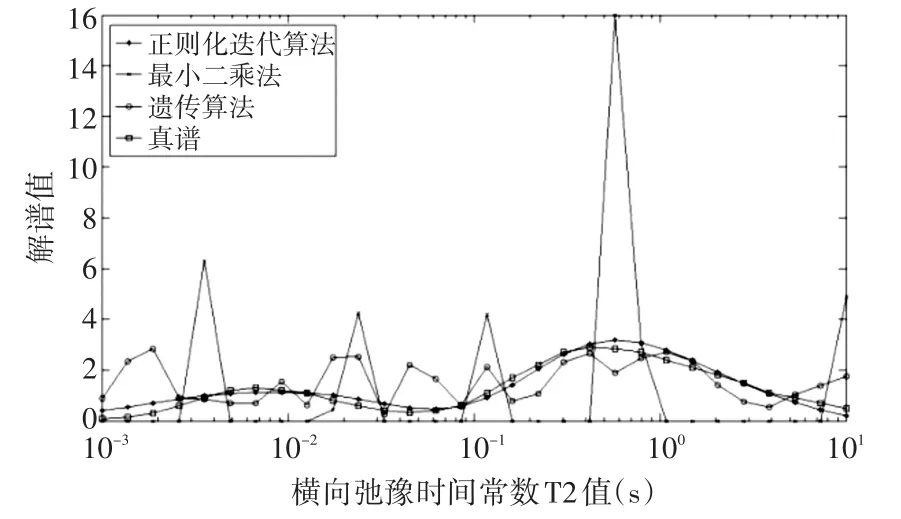
图2 三种不同算法解谱对比图（信噪比=25%）

表1 不同信噪比和算法误差表

6 岩心实验数据反演

在实验室以实测的某井岩心回波数据为T2谱反演模型的右端向量，回波间隔取TE=322.65+(i-1)×300，i的意义同式（6）。使用正则化迭代算法对其进行反演解谱，并与实验室某国外反演软件包的解谱结果进行了对比，如图3所示。

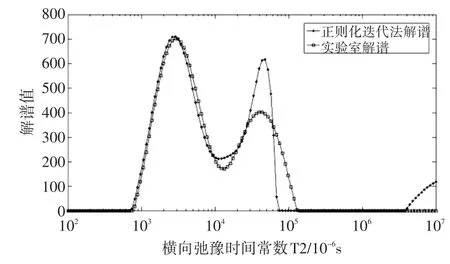
图3 某井岩心反演结果与实验室反演结果对比图

7 结语

对于有噪声的理论数据反演，对比图1和表1，可知在α一定的情况下，信噪比snr越大，数值解的精度越高，这个道理是很浅显的，因为信噪比snr越大，噪声对病态矩阵的影响越小，解的精度越高。对比图2和表1，可以得出，正则化迭代算法数值解的精度明显高于简单遗传算法和最小二乘法求解精度。这是因为对于病态线性方程组，如果不对系数矩阵改造，使之变为良态，在求解时右端向量的噪声或系数矩阵的误差会因系数矩阵病态性而被放大，从而导致数值解的误差非常大。正则化迭代算法是在对病态的系数矩阵改造成良态的基础上构成的迭代公式进行求解，所以解的精度得到了有效的提高。对于某井岩心实验数据反演结果，通过观察可以得知正则化迭代算法反演结果与实验室反演结果基本吻合，谱的形状与变化趋势基本一致。因此，正则化迭代算法是求解大型超定病态线性方程组的一种有效算法。