有限群的弱τσ-嵌入子群

王大山, 吴珍凤, 孔祥智, 杨南迎

(江南大学 理学院, 江苏 无锡 214122)

1 引言与预备知识

本文所有的群均为有限群,G总表示一个有限群, |G|表示G的阶, P表示全体素数的集合,π(n)为n的素因子集合,π(G)=π(|G|), |G|π表示整除|G|且素因子全在π中的最大整数.

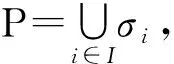
如果群G的子群H与G的任意Sylow子群P可置换, 则H称为在G中是S-置换的[3].如果子群H与G的任意满足(p,|H|)=1的Sylowp-子群P可置换, 则H称为在G中是S-半置换的[4]; 如果子群H与G的任意满足(p,|H|)=1且(|H|,|PG|)≠1的Sylowp-子群P可置换, 则H称为在G中是τ-拟正规的[5]; 如果存在群G的正规子群T, 使得HT在G中是S-置换的, 且H∩T≤HsG, 则群G的子群H称为在G中是S-嵌入的[6], 其中HsG是由所有含于H且在G中是S-置换的子群生成的群.如果存在G的正规子群T, 使得HT在G中是S-置换的, 且H∩T≤HτG, 则群G的子群H称为在G中是τ-嵌入的[7], 其中HτG是由所有含于H且在G中是τ-拟正规的子群生成的群.由定义知,S-置换子群、S-半置换子群、τ-拟正规子群和S-嵌入子群都是弱τ-嵌入子群, 但文献[7]中例1.3和例1.4表明反之不成立.

如果群G有一个完全Hallσ-集H, 使得对所有H∈H和所有x∈G, 均有AHx=HxA, 则群G的子群A称为在G中是σ-置换的[1].如果群G有一个完全Hallσ-集H, 使得对所有x∈G和所有满足σ(A)∩σ(H)=Ø的H∈H均有AHx=HxA, 则子群A称为在G中是半置换的[8].设H是群G的某个完全Hallσ-集, 令

τH(A)={σi∈σ(G)σ(A)|σ(A)∩σ(HG)≠Ø, 其中H是G的一个Hallσi-子群, 且H∈H }.

如果对H中满足σ(H)⊆τH(A)的子群H和所有x∈G, 均有AHx=HxA, 则子群A称为在G中关于H是τσ-拟正规的； 如果A关于G的某个完全Hallσ-集H是τσ-拟正规的, 则称子群A在G中是τσ-拟正规的[9].易见σ-置换子群和σ-半置换子群都是τσ-拟正规子群, 但文献[9]中例1.2表明反之不成立.

文献[1-10]利用上述概念和方法得到了一系列有限群结构的重要结果.通过分析上述已有的结果与方法, 再结合σ-置换子群和τσ-拟正规子群的概念, 本文引入如下概念.

定义1对于群G的子群H, 如果存在G的正规子群T, 使得HT在G中是σ-置换的, 且H∩T≤HτσG, 则H称为在G中是弱τσ-嵌入的, 其中HτσG是由所有含于H且在G中τσ-拟正规子群生成的子群.

注1如果σ是所有素数集合P的一个最小划分, 即σ={{2},{3},…}, 则弱τσ-嵌入子群即为弱τ-嵌入子群； 另一方面, 由定义1知τσ-拟正规子群也是τσ-弱嵌入的.但下列实例分别表明反之不成立.

例2令G=S4, 其中S4是4次对称群.设H=〈(14)〉,Q=〈(123)〉, 则H和Q分别是G的一个2阶子群和Sylow 3-子群, 设P是G的一个Sylow 2-子群.取σ={σ1,σ2,σ3}, 其中σ1={2},σ2={3},σ3={2,3}′, 则H={P,Q}是G的一个完全Hallσ-集.因为存在G的正规子群A4, 使得HA4=G且H∩A4=1, 所以H是G的弱τσ-嵌入子群.但H不是G的τσ-拟正规子群.事实上, 若H是G的τσ-拟正规子群, 则由σ2∈τH(H)知HQ=QH, 但经计算知显然HQ≠QH, 矛盾.

本文通过研究子群的弱τσ-嵌入性, 给出有限群是σ-可解和超可解的一些新的充分条件, 其中未说明的概念和符号可参见文献[11-12].

引理1[1]所有σ-可解群的子群和商群都是σ-可解的, 任意两个σ-可解群的直积也是σ-可解的, 并且任意σ-可解群被σ-可解群的扩张还是σ-可解群.

引理2[13]令H,R,K是群G的子群, 其中R≤K,H在G中是σ-置换的且R是G的正规子群, 则有:

1)HR/R在G/R中是σ-置换的；

2) 如果G是具有Sylow型的σ-完全群, 则H∩K在K中是σ-置换的；

3) 如果G是具有Sylow型的σ-完全群, 且K/R在G/R中是σ-置换的, 则K在G中是σ-置换的.

引理3设G是σ-完全群,A是G的一个子群, 则有:

1) 如果A是群G的一个σ-次正规子群且A是一个Π-群, 则A≤OΠ(G)[13]；

2) 如果A在G中是σ-置换的, 则A在G中是σ-次正规的[1];

3) 如果A是G的一个σ1-子群, 则A在G中是σ-置换的当且仅当Oσ1(G)≤NG(A)[1].

引理4[9]设G有一个完全Hallσ-集H={H1,…,Ht}, 使得G的子群H和K在G中均为关于H是τσ-拟正规的.令R是G的正规子群且H≤L≤G.则有：

1) H0={H1R/R,…,HtR/R}是G/R的一个完全Hallσ-集, 并且如果σ(H)=σ(HR/R), 则HR/R在G/R中关于H0是τσ-拟正规的；

2) 如果HK=KH且σ(H∩K)=σ(H)=σ(K), 则H∩K在G中关于H是τσ-拟正规的；

3) 如果L∩H={L∩H1,…,L∩Ht}是L的一个完全Hallσ-集, 则H在L中关于L∩H是τσ-拟正规的；

4) 如果G是具有Sylow型的σ-完全群, 则H在L中是τσ-拟正规的.

下面给出弱τσ-嵌入子群的性质.

引理5设群G是具有Sylow型的σ-完全群,H是群G的一个弱τσ-嵌入子群,U≤G且N是G的正规子群.则有：

1) 如果H≤U, 则H在U中是弱τσ-嵌入的；

2) 如果H是一个σi-子群且N≤H, 则H/N在G/N中是弱τσ-嵌入的；

3) 如果(|H|,|N|)=1, 则HN/N在G/N中是弱τσ-嵌入的.

证明： 因为H在G中是弱τσ-嵌入的, 所以存在G的正规子群T, 使得HT在G中是σ-置换的, 且H∩T≤HτσG.

1) 因为T∩U◁U且H(T∩U)=HT∩U, 由引理2中2)知,H(T∩U)在U中是σ-置换的.由引理4中4)知,H∩(T∩U)=H∩T≤HτσG≤HτσU.因此H在U中是弱τσ-嵌入的.

2) 因为TN/N◁G/N且(H/N)(TN/N)=HT/N, 由引理2中1)知,HT/N在G/N中是σ-置换的.又因为σ(H)=σ(H/N)={σi}, 所以由引理4中1)知，

(H/N)∩(TN/N)=(H∩T)N/N≤HτσGN/N≤(HN/N)τσ(G/N).

因此H/N在G/N中是弱τσ-嵌入的.

3) 因为TN/N◁G/N, 由引理2中1)知, (H/N)(TN/N)=HTN/N在G/N中是σ-置换的.又因为

(|N∩HT∶N∩H|,|N∩HT∶N∩T|)=(|(N∩HT)H∶H|,|(N∩HT)T∶T|)=1,

故N∩HT=(N∩H)(N∩T).由文献[11]中引理1.2知,HN∩TN=(H∩T)N.显然σ(HτσGN/N)=σ(HτσG), 故由引理4中1)知

(HN/N)∩(TN/N)=(H∩T)N/N≤HτσGN/N≤(HN/N)τσ(G/N).

因此HN/N在G/N中是弱τσ-嵌入的.

引理6[14]令H,K,N是群G的两两可置换的子群, 并且H是群G的Hall子群, 则N∩HK=(N∩H)(N∩K).

引理7[15]设A,B是群G的非平凡子群, 使得G≠AB, 并且对所有的x∈G, 均有ABx=BxA, 则G有一个真正规子群N, 使得A≤N或B≤N.

引理8[16]令N是群G的正规子群, 且S为G的具有下列性质的子群:

1)N∩S≤Φ(S)； 2) (|N∩S|,|G∶S|)=1.

假设π为|N∩S|的素因子集合, 则存在N的正规子群M, 使得M∩S=1,N/M是π-群, 且|N∩S|整除|N/M|.

2 主要结果

定理1设G是具有Sylow型的σ-完全群, 且H={H1,…,Ht}是G的一个完全Hallσ-集.令|G|的最小素因子p∈σ1.如果H1是超可解的, 且H1的每个极大子群在G中均是弱τσ-嵌入的, 则G是σ-可解的.

证明： 用反证法.假设结论不成立, 设G是极小阶反例, 则t>1.由Feit-Thompson定理[16]知,p=2∈π(H1).不失一般性, 对于所有i=1,2,…,t, 设Hi是一个σi-子群.

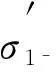
|H1R/R∶M/R|=|H1R/R∶(M∩H1)R/R|=|H1∶M∩H1|

是一个素数, 进而M∩H1是H1的一个极大子群.由定理假设和引理5中3)知,M/R=(M∩H1)R/R在G/R中是弱τσ-嵌入的, 表明G/R满足定理假设.从而由G的选取知G/R是σ-可解的.又由Feit-Thompson定理知,R是可解的.因此由引理1知G是σ-可解的, 矛盾.故2)成立.

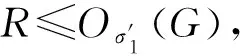
4)G有唯一的极小正规子群, 记为R.由3)知,G=RH1对于G的任意非平凡极小正规子群R都成立.因此由G/R=RH1/R≅H1/(H1∩R)是σ-可解的及引理1知,G有唯一的极小正规子群, 记为R.

如果T≠1, 则R≤T.因为L∩R≤L∩T≤LτσG≤L, 所以L∩R≤LτσG∩R≤L∩R, 表明L∩R=LτσG∩R.又因为

|H1∩R∶L∩R|=|(H1∩R)L∶L|=|H1∶L|,

且H1是超可解的, 所以L∩R≠1.下面令Rj是R的任意非平凡Hallσj-子群, 其中j≠1.由G=RH1知,Rj也是G的一个Hallσj-子群.设A≤LτσG, 且A在G中是τσ-拟正规的.因为

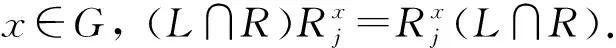
|R/N|σ1=|R|σ1/|N|σ1=|H1∩R∶H1∩N|||H1∩R∶L∩N|,

定理2设G是具有Sylow型的σ-完全群, 且H={H1,…,Ht}是G的一个完全Hallσ-集, 使得对所有i=1,2,…,t,Hi是G的超可解σi-子群.如果对任意的非循环子群Hi的每个极大子群都在G中是弱τσ-嵌入的, 则G是超可解群.

证明： 用反证法.假设结论不成立, 并设G是极小阶反例.

1)G是可解的.设p是整除|G|的最小素数, 不妨假设p∈π(H1).如果H1是循环的, 则G的Sylowp-子群是循环的, 由文献[16]中定理2.8知,G是p-幂零的, 从而G是可解的.如果H1是非循环的, 则由定理1知,G是σ-可解的.令H/K是G的任意一个主因子, 则H/K是σ-准素的.不失一般性, 设H/K是一个σi-群.因为H/K≤HiK/K≅Hi/(Hi∩K), 所以H/K是超可解的, 从而是一个初等交换r-群, 其中r是素数.由H/K的任意性知G是可解的.故1)成立.

|HiR/R∶L/R|=|HiR/R∶(L∩Hi)R/R|=|Hi∶L∩Hi|

是一个素数, 从而L∩Hi是Hi的一个极大子群.根据定理假设和引理5中3)知,L/R=(L∩Hi)R/R在G/R中是弱τσ-嵌入的.表明定理假设对G/R成立.从而由G的选取知G/R是超可解的.因此2)成立.

3)R是G的唯一极小正规子群,Φ(G)=1,R=Op(G),R是一个初等交换p-群且|R|>p, 其中p是素数.由1)和2)直接可得3).

如果T=1, 则L在G中是σ-置换的, 由引理3知,L≤Oσ1(G)≤H1.但L是H1的极大子群, 故L=Oσ1(G)或Oσ1(G)=H1.如果L=Oσ1(G)◁G, 由3)知R≤L或L=1.如果R≤L, 与L的取法矛盾.因此L=1, 从而L=Oσ1(G)=1, 进而R=1, 矛盾.表明Oσ1(G)=H1◁G.因为L在G中是σ-置换的, 所以对所有i≠1, 均有LHi=HiL.故LHi∩H1=L(Hi∩H1)=L.从而Hi≤NG(L), 进而Hi≤NG(L∩R)=NG(E).又因为H1≤NG(E), 所以G≤NG(E), 即E◁G, 从而E=1, |R|=p, 矛盾.

LτσGHi∩R=(LτσG∩R)(Hi∩R)=LτσG∩R=L∩R=E,

从而对所有i≠1均有Hi≤NG(E).又因为H1≤NG(E), 所以E◁G.从而E=1, |R|=p, 矛盾.证毕.

由定理2直接可得如下推论.

推论1[16]如果G的每个Sylow子群都是循环的, 则G是超可解的.

推论2[17]如果G的每个Sylow子群的极大子群在G中是正规的, 则G是超可解的.

推论3[17]如果G的每个Sylow子群的极大子群在G中是S-置换的, 则G是超可解的.

推论4[18]如果G的每个Sylow子群的极大子群在G中是c-正规的, 则G是超可解的.

推论5[19]如果G的每个非循环Sylow子群的极大子群在G中是S-嵌入的, 则G是超可解的.

推论6[20]设G是一个群, 如果G的每个Sylow子群的极大子群在G中是弱τ-嵌入的, 则G是超可解的.