基于组合导航系统的智能汽车精准定位

史 骏

（西安铁路职业技术学院机电工程系 西安 710026）

1 引言

智能汽车是集成环境感知、路线规划、智能决策和负责驾驶等多种功能的综合系统，是未来缓解交通拥挤、降低交通事故的重要解决方案。智能汽车得以安全行驶的重要前提是实现对智能汽车精准的导航定位。

目前智能汽车常用的导航定位技术有卫星导航定位技术、惯性导航技术等。卫星导航定位技术是通过接受GPS、CNSS等卫星导航系统的数据信息获取车辆准确位置信息以及行驶路径、方向实现方位导航。由于卫星导航系统的接受装置容易受到干扰导致不能稳定正确定位，因此卫星导航系统不能独立应用于智能汽车的实时导航。

惯性导航系统是通过对陀螺仪和加速度计等传感设备采集的速度、姿态角、位移量等数据进行一系列计算，得出当前导航信息。惯性导航具有系统独立、抗外部干扰能力强、无需接受信号的优点，但是长时间运行其导航定位的累计误差较大，需要与其他导航系统配合使用。

基于上述考虑，本文提出一种基于组合导航的智能汽车精准定位系统。该系统基于组合导航原理，采用分散滤波、混合校正以及改进滤波算法等技术，对GPS的导航数据和惯性导航的定位数据进行融合计算，最终输出精度较高的导航定位数据。

2 组合导航定位原理

本文所述的组合导航系统是采用对GPS和惯性导航系统的组合，利用组合滤波器对GPS的原始定位数据和惯性导航的输出定位数据进行滤波处理，然后将误差数据反馈至惯性导航模块，最后由惯性导航模块输出经过反馈校正的定位数据输出，实现智能汽车精准定位。组合导航原理如图1所示。

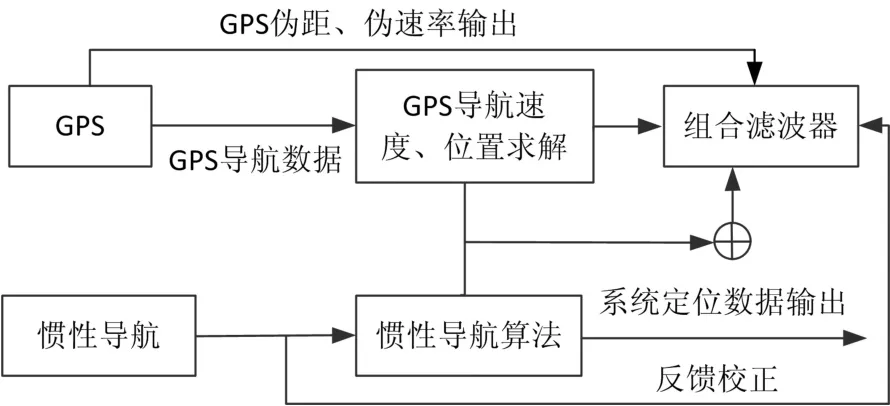
图1 组合导航原理图

由GPS和惯性导航组成的导航系统的平台误差角的计算公式如式（1）所示。

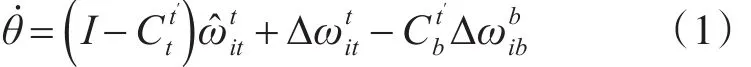
式（1）中θ表示误差角。速度误差计算公式如式（2）所示。

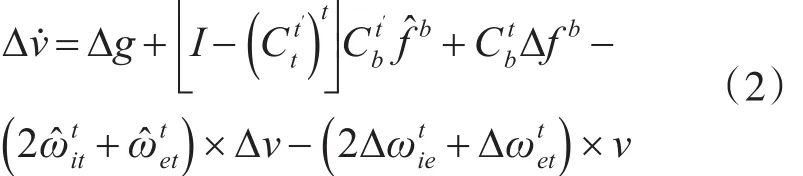
式（2）中Δv表示速度误差。位置误差的计算公式如式（3）所示。

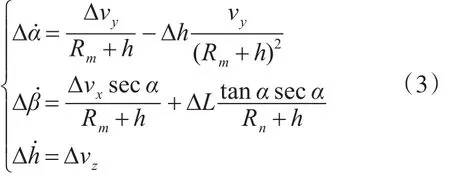
式（3）中 α、β、h分别表示维度、经度和高度。上述公式中=[aij]。i。j=1。2。3 ，aij的具体数值如式（4）所示。

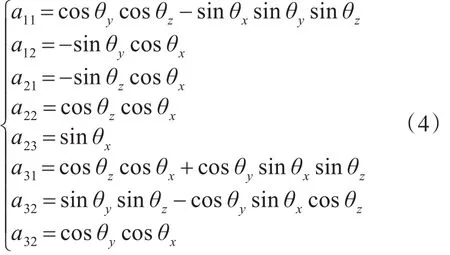
式（4）中 θx。θy。θz分别代表东、北、西方向的角度偏差。表示姿态误差。表示加速度传感器的输出数值。表示加速度传感器的测量误差。Δg为重力加速度的计算误差。Rm和Rn分别表示子午圈与卯酉圈主曲率半径。

式（1）、式（2）和式（3）组成组合导航系统的状态方程。

我就不信爬不上去。哎哟，这钢角刺真扎人。哎哟，痛死我了，他娘的。宝刚一边骂骂咧咧，一边曲里八拐往上爬，还别说，真让他上去了。宝刚那个喜呀，乱蹦乱跳好一阵才开始砍柴。很快就砍满了一担。宝刚将柴用葛藤捆好，然后顺着陡墈往下推，推第一捆还好，推第二捆的时候，宝刚没站稳，人就顺着那捆柴滚下去了，从此，落下了终身残疾。

组合导航系统的误差方程为式（5）所示。

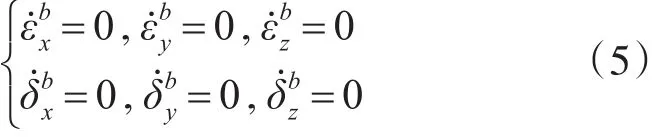
式（5）中εb为常值零偏，δb为常值漂移。

3 分散式滤波和混合校正技术

组合导航系统中的滤波器由全局滤波组件和局部滤波组件组成，其设置方式如图2所示。

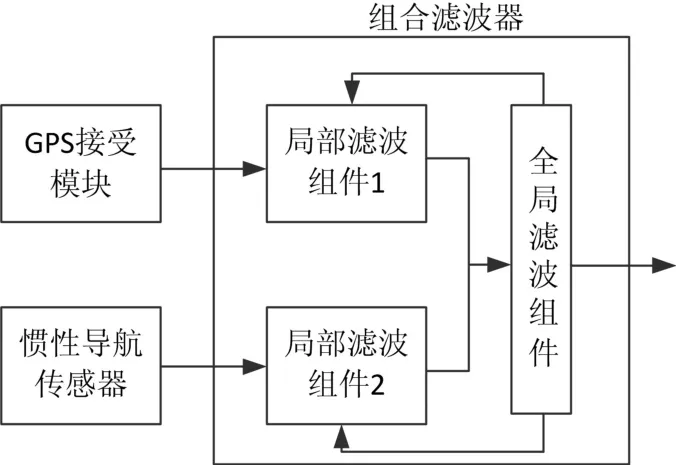
图2 分散式滤波

由于组合滤波器分散为局部滤波组件和全局滤波组件两个部分，所以其滤波计算分为两个过程。第一个计算过程是由相应的局部滤波组件对各个局部导航系统的导航定位数据进行计算，得出局部导航系统的定位信息；第二个过程是由全局滤波组对局部滤波组件的定位信息进行融合计算，得出最终的定位信息。在此过程中局部导航系统的定位计算得到了并行处理和重复优化，因此组合导航系统的定位效率和定位精度也得到了提高。

组合导航系统中，采用混合输出校正和反馈混合的校正方式对滤波器计算出的导航参数误差值进行校正。

在滤波器工作的初始阶段，由于初始状态值和噪声初值的选取偏差较大，导致滤波器计算出估值偏差也较大，如果直接反馈到惯性导航中，会导致系统输出误差偏大，精度降低，因此在滤波器工作初始阶段采用输出校正和滤波器反馈校正相结合的方式，并且将输出校正的速度设置为高于滤波器反馈校正反馈的速度。等到滤波器进入稳定工作阶段，就去掉输出校正，采用滤波器反馈校正方式对惯性导航系统的输出误差纠偏。这种校正方式能够最大限度保证组合导航系统的定位精度。

4 改进的容积卡尔曼滤波算法

容积卡尔曼滤波算法是基于状态值和测量值的正态分布的考虑，利用上一时刻的最优估算值和当前时刻的测量值的融合计算得出当前时刻的最优定位结果。容积卡尔曼滤波算法的基础是系统状态值和测量值服从没有任何耦合的正态分布规律，分布点均匀分布在以原点为中心的球的表面，且分布点的个数是状态值的2倍。以此为前提，依据容积准则可以确定的均差和方差是可以估算出系统的当前最优定位数据。而在前提条件充分的基础上，容积卡尔曼滤波问题则变成对由非线性函数和正态分布的噪声方程联立的积分函数进行计算的问题，其中噪声的正态积分权重可由容积准则来确定。

正态加权积分的计算过程如下所示。

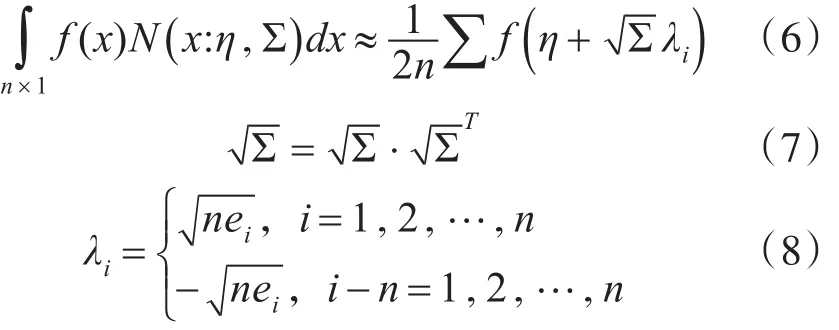
其中式（8）中ei是单列矢量的第i个元数据。此方法对线性正态加权积分函数具有较高的计算精度。

容积卡尔曼滤波算法包括时间更新算法和输出更新算法。时间更新算法如图3所示。

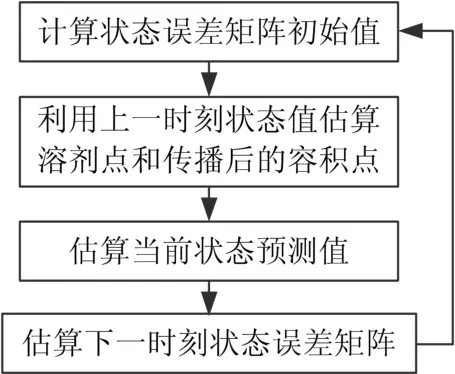
图3 时间更新算法

输出更新算法如图4所示。

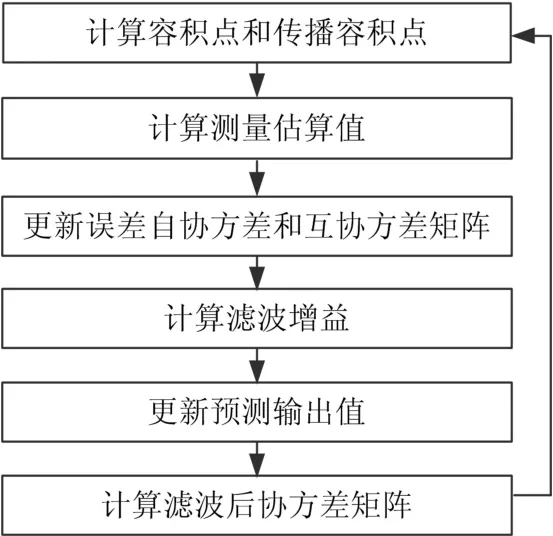
图4 输出更新算法

容积卡尔曼滤波算法在面对线性模型时有较强的输出精度和运行稳定性，但是由于面对组合导航的计算模型的非线性和以及噪声变化的不确定性会导致该算法输出精度下降，甚至会出现滤波发散、定位失败的问题。为此通过引入渐消系数λ对滤波后协方差矩阵进行及时调整，使得输出的误差序列能够保持相互正交，提高滤波器的误差跟踪的能力。

渐消系数λk依据式（8）计算得出。

式（8）中相关参数的计算方法如下所示。

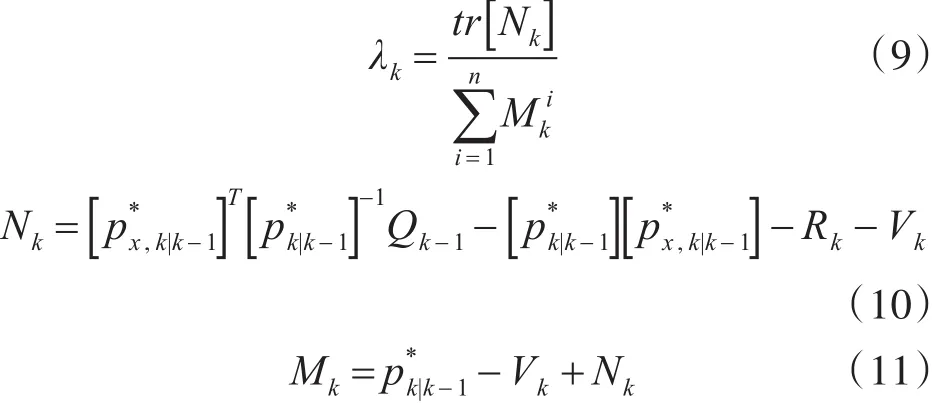
式（9）、式（10）和式（11）中标识*的变量表示是引入渐消系数λk之前的值。

将上述渐消系数运用到滤波算法中的状态预测协方差矩阵中的具体算法为

第一步，计算初始误差数据和预测误差。然后按照上文时间更新算法和输出更新算法计算出误差自协方差矩阵和互协方差矩阵。并将计算出的变量打上*标识。

第二步，按照式（9）～式（11）计算出渐消系数 λk。

第三步，将λk引入误差协方差矩阵Pk|k-1。

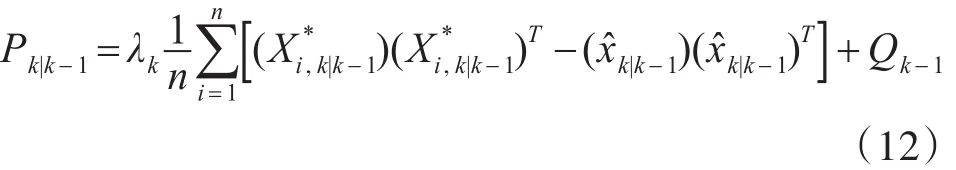
第四步，重新计算误差协方差矩阵等滤波参数。

第五步，重新计算滤波增益、预测输出值和滤波后误差协方差矩阵。

5 仿真分析

仿真测试针对独立GPS导航系统和组合导航系统进行定位精度测试。其中两个导航系统的滤波器均采用本文所述的改进滤波算法。

仿真系统的参数设置如表1所示。

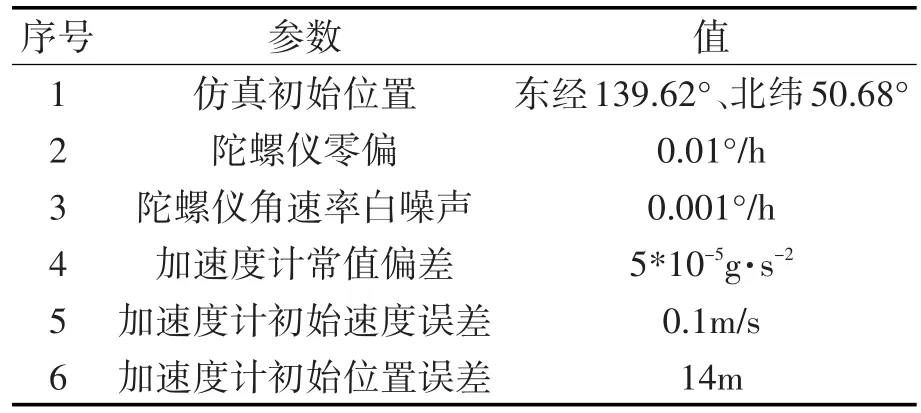
序号 值123456参数仿真初始位置陀螺仪零偏陀螺仪角速率白噪声加速度计常值偏差加速度计初始速度误差加速度计初始位置误差东经139.62°、北纬50.68°0.01°/h 0.001°/h 5*10-5g·s-2 0.1m/s 14m

仿真时间为10min。仿真结果如图5所示。

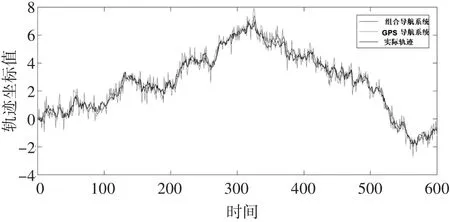
图5 仿真结果

由图5可以看出，基于GPS和惯性导航的组合导航系统定位的轨迹线更加贴近实际轨迹，而且其定位轨迹线的噪声也要小于GPS导航系统，因此基于GPS和惯性导航的组合导航系统的定位精度明显优于GPS导航系统。

6 结语

本文对基于GPS和惯性导航的组合导航原理进行深入研究，对组合导航系统中分散滤波方法、混合校正技术以及滤波算法进行了重点阐述，最后通过仿真分析证明了该导航系统能够为智能汽提供精度明显优于单个导航系统的车辆精确定位服务。