混合条件属性的细化类别特征粒度系数聚类算法

周 靖

（广东石油化工学院计算机与电子信息学院 茂名 525000）

1 引言

混合条件属性数据集是在同一个数据集中，同时存在分类条件属性［1］和数值条件属性［2］特征参数。混合条件属性数据集的复杂性广泛存在于实际应用领域中，如网络入侵检测、金融欺诈检测、天气预报、垃圾邮件识别等［3］。由于混合条件属性包含的分类和数值特征参数的取值范围、类别特性存在较大的差异，传统针对单一条件属性的聚类算法已不适合处理混合条件属性对象，如何有效地规范混合条件属性数据集的聚类过程是时下许多研究者面临的重大挑战。

针对混合条件属性数据集的聚类分析，近年来，学者们提出了很多优化算法。K-Protoypes［4～5］是处理混合条件属性数据的经典算法，该算法采用欧式距离度量数值条件属性特征参数间的相似性，采用差别度匹配的方式处理分类条件属性特征参数间的相似性。Hsu、Chen提出的CAVE算法［6］和文献［7］均提出对分类条件属性采用特征参数点熵度量，或配合层间距离计算相异度，对数值条件属性则采用方差或各种距离测度计算方法来衡量相似性。文献［8］通过定义条件语义属性的相异性距离测量，提出一种基于数据内在混合结构的熵聚类SEC算法。文献［9］对数据流的展现形式进行了区分，微聚类中采用针对维度的距离形式衡量相似性，在宏聚类中则采用变化了的密度聚类算法来处理微簇聚类。文献［10］将混合属性数据分为数值占优、分类占优和均衡三类形式，根据核心点确定密度关联的实际对象来实现聚类。文献［11］采用分别考虑属性距离及关系强度的密度聚类方法，综合处理条件属性的关系及关系强度信息。由David等提出的SpectralCAT［12］算法，将数值条件属性通过最优检测，利用谱聚类转化为分类条件属性，以牺牲特征信息为代价达到统一混合条件属性的目的。文献［13］提出了一种面向不平衡数据的迭代特征加权聚类算法，其依据每次迭代过程中，聚类簇的特征及类别特性重要性的衡量函数，确定条件属性的特征权重。这类加权算法在混合条件属性数据集中的聚类表现优越。SBAC［4］算法思想来源于生物遗传的分类问题，是一种围绕凝聚性层次聚类的聚类算法，其优点是能呈现混合条件属性中内聚性较大的簇。综合上述研究，提出现有的对混合条件属性对象的聚类算法存在以下缺陷：

1）鉴于混合条件属性对象的特点在于由分类和数值条件属性两类特征形态完全不同的特征参数共同组成，大部分算法对混合条件属性特征参数采取了“分而治之”的思想，在对两类条件属性特征参数相似性计算上，几乎不存在任何相同的、相关的处理点。但混合条件属性对象的组合形式对同一类别的共同指向，又意味着两类特征参数对类别特征的显示必然存在着相对或绝对的关联，绝对的“分而治之”，对两类特征参数所呈现出的类别特性的量化值，会存在较大的偏差，从而影响聚类的性能。

2）当混合条件属性个数比例不平衡时，其所对应的特征参数也呈现不平衡的特性，而普通的类别特性加权方式往往忽略比例较低的条件属性。而当混合条件属性个数相对接近时，其所对应的特征参数对类别特性的呈现又会出现界定模糊的弊端，包括太多的特征噪音。

为了降低不同条件属性间不同形式的处理方式所带来的累积误差，提出混合条件属性的细化类别特征粒度系数聚类算法（Refining Category Char⁃acteristics Granularity Coefficients Clustering，RCC⁃GR-C）。其聚类核心在于对分类（熵定义类别凝聚性）和数值（欧式距离定义相似性）条件特征参数相对“分而治之”的前提下，引入细化类别特征粒度系数，关联两者特征对象对类别特性共同形态的呈现，并最终通过迭代稳定系数的权重。

2 基于细化类别特征粒度系数的类别凝聚性概念描述及其分析

在介绍算法之前，先给出相关新算法的概念描述。概念中主要引入细化类别特征粒度系数的形式，关联混合条件属性间的相关类别特征。

定义 1 设数据集 S 记为 S=｛X1，X2，…，Xi，…，Xm｝=Sm×n，即S含有m个混合属性数据对象，n表示对象的混合属性数目。其中，任一Xi记为｛xi1，xi2，…，xip，x（i，p+1），x（i，p+2），…，xin｝，前 p个元素是数值条件属性值，其它是分类条件属性值。

定义2 针对分类条件属性，若S初始化为t个簇，则xij在第j个分类条件属性下的类别凝聚性记为V（xij），其采用信息熵的形式描述，定义如下：

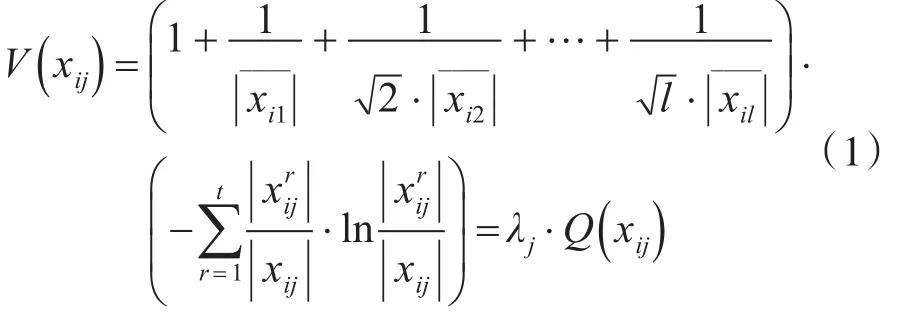
其中， ||xij是属性值xij在分类条件属性j下出现的次数，是xij在分类条件属性j下、第r簇中出现0；λj为类别特征细化粒度系数，直接面向数据集中从小到大的序列，下标值并不遵循原始条件属性的维度顺序；1。2。…。l是自然数等差数列，l≤p，

定义3 针对p个分类条件属性，Xi面向t个簇的分类粒度级别定义如下：

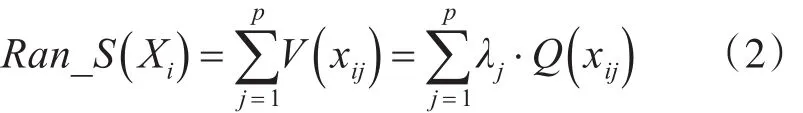
在类别凝聚性V（xij）的计算策略上，由于簇与簇之间的原始特征存在较大的差异，会造成V（xij）数值量级不在同一级别上，且数值级别趋向陡度大、不稳定的结果。鉴于对象特征值分布比例是最能体现类别特征的指标之一，因此引入λj，在计算过程中尽可能地对类别特征不明显的小簇设置细化程度较高的类别粒度级别，对大簇设置细化程度较低的类别粒度级别，即是对信息熵转换的类别特征值进行细化调整。

对λj的有效性验证，即证明λj存在于一个确定区间，且其取值范围为( )0。2 p ，验证如下。

也就是当p=k+1时，不等式成立。因此，由上述两种情况，不等式对任意自然数p都成立。所以，λj的最大值小于2 p，证毕。

定义4 针对数值条件属性，若S初始化为t个簇，则每个簇中心 Yi记为｛yb1，yb2，…，ybp，y（bp+1），y（b，p+2）…，yin｝，Xi与 Yi中任一数值条件属性采用特征参数值的欧氏距离计算形态，来描述数值条件属性部分的类别凝聚性，定义如下：定义5 针对数值条件属性，Xi面向t个簇的分类粒度级别定义如下：

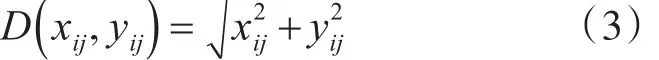
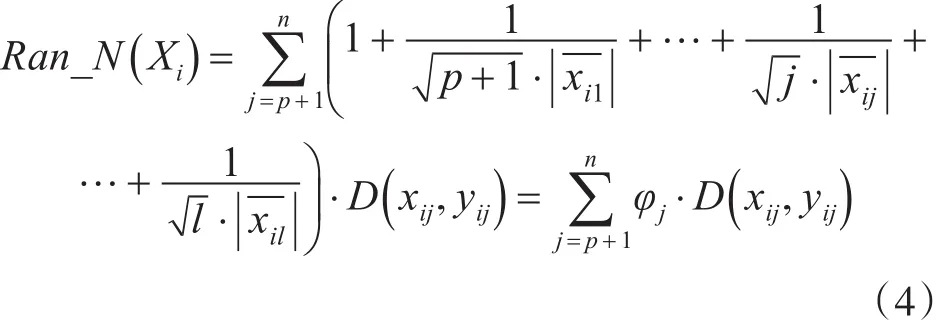
其中，φj是数值条件属性的整体类别细化粒度调整参数，其所有粒度变量的说明同式（1），且有效性验证参见λj的证明过程。

定义6 Xi面向t个簇的整体分类粒度级别，即合并式（2）和式（4），定义如下：

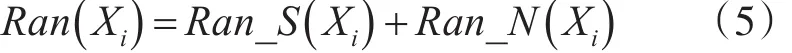
3 聚类算法策略设计

基于细化类别特征粒度系数聚类算法的基本步骤如下：

第1步 将数据对象集合D随机分为k个簇，并在每个簇中随机标注任一数据对象Xy作为簇中心，得到k个簇中心集合{X1。…。Xy。…。Xk}。

第2步 从k个簇中随机选择一个未被标注的数据对象Xi，标注它。

第3步 针对分类条件属性，逐个计算Xi的p

第4步 对第y个簇的簇中心Xy，遵循第3步得到 Ran_S（Xy）。

第5步 针对数值条件属性，逐个计算Xi的

第6步 对任意Xy，遵循第5步得到Ran_N（Xy）。

第7步根据式（5）计算Ran（Xi）和Ran（Xy），并计算增量值 SE=Ran（Xi）-Ran（Xy），若 SE＞0，Xi替换Xy成为第y个簇的簇中心，并撤销Xy的簇中心标注；若SE≤0，从D中随机选择任意数据对象，重复第2步至第7步。

第8步 直到所有SE均为正，算法结束。

围绕上述步骤，分析RCCGR-C算法的时间复杂度。算法簇中心的划分的计算成本为O（kmn）；R=MAX（tp）及O（p2）分别表示针对分类条件属性，类别凝聚性计算中单个不同特征值在t个簇中呈现不同值得最大数量及λj粒度变量排序过程的计算成本；O（km（n-p））表示针对数值条件属性欧式距离方法的基本计算成本，O（（n-p）2）为 φj粒度变量排序过程中的计算成本；w是算法整体要求收敛所需的迭代次数。因此，RCCGR-C算法的时间复杂度为O（（2kmn+tp+2p2-kmp+n2-2np）w）。

4 实验及结果分析

4.1 实验环境及数据

所有实验均在一台高性能配置PC机上运行，配置如下：酷睿i7-4790 CPU，DDR3 8G内存，1TB硬盘，WIN7操作系统，并采用Matlab结合Visual Stdio 2010中VC++的运行环境实现。实验数据出自 http：//archive.ics.uci.edu/ml/datasets.html的 UCI数 据 集 ，采 用 Adult、Chess、Credit Approval及Hear-Disease混合条件属性数据集。Adult共48842个数据对象，14维条件属性，其中分类条件属性8维，数值条件属性6维，分为2类；Chess共28056个数据对象，6维条件属性，其中分类条件属性3维，数值条件属性3维，分为17类；Hear-Dis⁃ease共303个数据对象，13个条件属性，其中分类条件属性8维，数值条件属性5维，分为5类；Credit Approval共690个数据对象，16维条件属性，其中分类条件属性10维，数值条件属性6维，分为2类。实验数据中包含大规模、高维、低维、小型等数据对象，适用于验证算法的伸缩性，且Credit Ap⁃proval和Hear-Disease数据集含缺省特征参数值。

4.2 λj及φj参数的聚类性能验证

伸缩性是指聚类算法除了有针对性地能在特定数据规模、数据格式的样本集中性能表现优异之外，面对混合条件属性的复杂数据环境，算法依旧能够保持有效的聚类性能。RCCGR-C算法中λj、φj参数是关键，主要起到对性能伸缩性调节的作用。实验过程中，对Adult的8维分类条件属性，粒度变量取值范围，即l取值从1～8，其中合的形态有=1种；（7，8）表示若l的取值为 7，所示，RCCGR-C与不接入λj系数的聚类算法（With⁃out Refining Category Characteristics Granularity Co⁃efficients Clustering，WRCCGR-C）分类属性部分聚类性能对比如图2所示。其中WRCCGR-C算法在策略设计中忽略了λj系数的计算过程。对Adult的性能间的关系如图3所示，RCCGR-C与不接入φj系数的聚类算法WRCCGR-C数值属性部分聚类性能对比如图4所示。由于数值条件属性数字量级、数字变化的多样性，实验中取数值条件属性特征参数值小数点后有效数字两位，且CC算法在策略设计中忽略了φj系数的计算过程。另外，对聚类准确率的计算，采用由Huang和Ng提出的评估标准［14～15］。

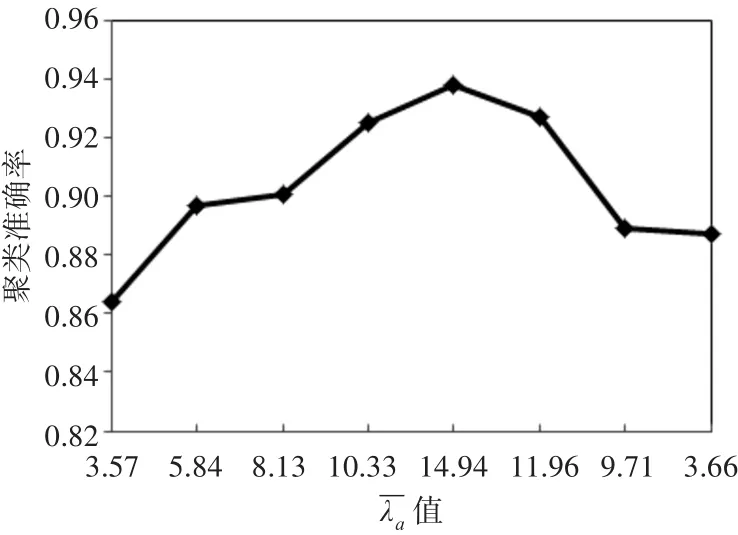
图1 RCCGR-C中λj的聚类性能

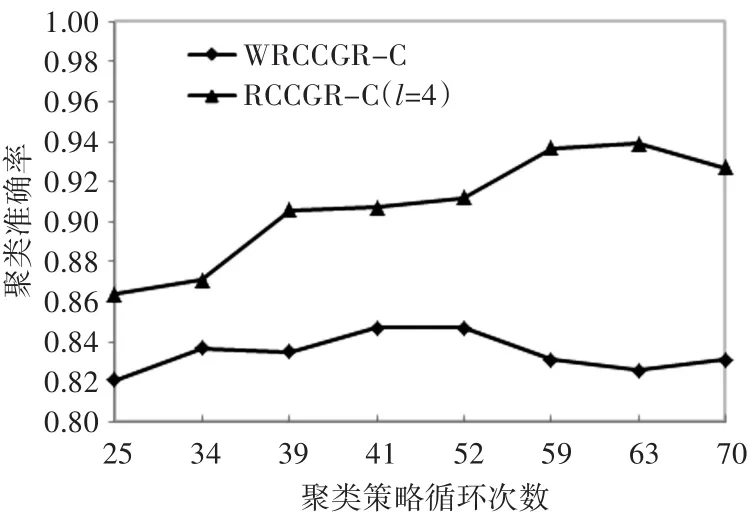
图2 WRCCGR-C与RCCGR-C（分类条件属性）的聚类性能

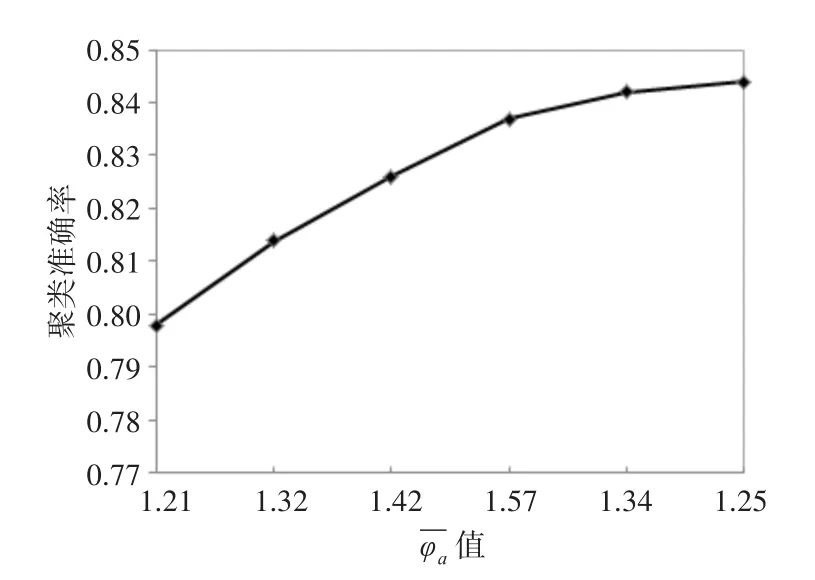
图3 RCCGR-C中φj的聚类性能

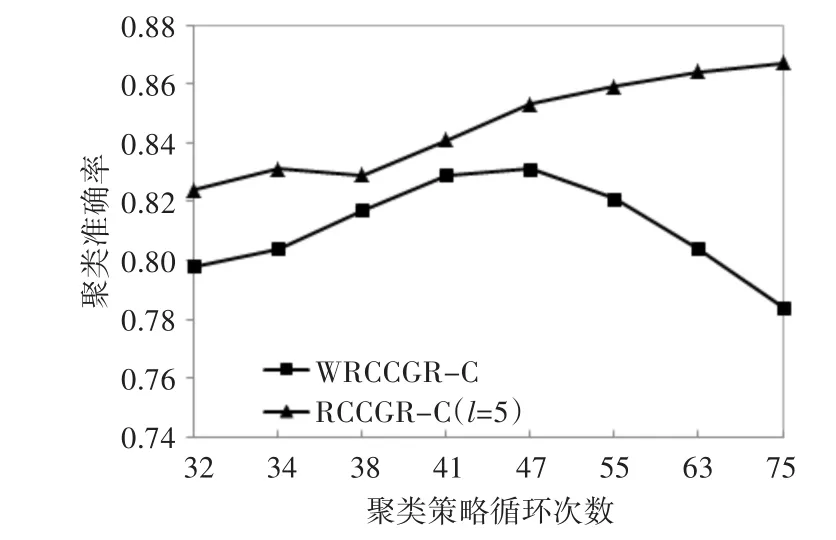
图4 WRCCGR-C与RCCGR-C（数值条件属性）的聚类性能

从图1可以看出，针对分类条件属性，l为8（涵盖所有分类条件属性）时，聚类准确性并不是最高的，甚至低于 l取值 3 时的情况，但当 l=4（ -λa=14.936）时，聚类准确性大幅度提高的陡度体现出λj系数突出的类别特征甄别能力。图3显示，针对数值条件属性，l=6时，聚类准确性也不是最高的，当l=3（-φa=1.42）时，聚类准确率最高陡度值出现。这说明在实际情况中，完整的数据样本中存在类别特征的混淆噪音很大，λj和φj在很大程度上能剔除不相关甚至干扰聚类的性能类别特征。对比图1和图3，针对Adult数据集，分类条件属性对类别特征甄别的贡献程度更高。图2中，RCCGR-C算法中l取值4，随着聚类循环次数的增大，聚类准确率达到最高值后逐步趋于稳定，与剔除λj系数的CC算法相比较，平均聚类准确率提高了将近7个百分点，算法体现出较强的稳定性。图4中，RCCGR-C算法中l取值5，随着循环次数的增大，聚类准确率也逐步提高，与剔除φj系数的WRCCGR-C算法相比较，平均聚类准确率也提高了3个百分点。显然，λj及φj参数的设置在某种程度上相对关联了两类“分而治之”的条件属性的类别特性，且在分类条件属性个数与数值条件属性个数比例相近时，条件属性类别特性的界定也较为清晰，噪音剔除效果优良，能有效提高聚类性能。但就Adult而言，系数设置对数值条件属性类别特征抽取的敏感度明显低于分类条件属性，因而图4的聚类准确率低于图2的描述。

4.3 RCCGR-C与其它算法的比较

实验选取了K-prototypes算法、GAVE算法和SBAC算法作为研究比较对象。从表1可以看出，RCCGR-C算法对混合条件属性数据集的聚类效果是明显的，且伸缩性能优越，适用于大、小规模的数据集。RCCGR-C对数据集的平均聚类精度能达到90%以上，说明在每一轮循环聚类后，RCCGR-C中的类别特征细化粒度系数会动态地调整不同簇中混合条件属性的综合类别特性，同时相应地统一归纳混合特征参数的类别贡献程度，使得条件属性个数、类别特征显著的一方的混合特征特性敏感度上升（更有利于混合特征特性的界定），不明显的一方的混合特征特性敏感度下降（减少忽略重要的类别特征的几率）。同时，避免常规聚类算法过度偏向包含过度特征噪音的大簇，而忽视类别特性更纯粹的小簇的缺陷。因此，RCCGR-C对混合条件属性数据的聚类性能，相比其它聚类方法，具有一定的优越性。相对而言，其它三种算法，尤其对缺省特征值的Credit Approval和Hear-Disease数据集的动态适应调整能力较差，聚类精度都在80%以下，受样本大小和类别质量的影响，体现出较弱的聚类性能。从算法效率的角度看，RCCGR-C聚类效率优势并不明显，这与其时间复杂度都属于O（n2）级有关，但仍高于CAVE，且与K-prototypes算法接近。

表1 RCCGR-C算法与其它聚类算法在四类数据集上的实验结果

5 结语

针对混合条件属性数据的类别特征特点，本文提出RCCGR-C伸缩性聚类算法。通过配置类别特征细化粒度系数，统一分类条件属性和数值条件属性对类别特征的描述形式，合理呈现条件属性类别特征权重。通过理论和实验分析，RCCGR-C算法对不同的数据集是有效的，具备了较强的伸缩性。而对类别特征细化粒度系数及相关的粒度变量的扩展与优化是后续需要研究的工作。