基于运动学非完整约束的里程计参数在线辨识

宋金龙，石志勇，王律化，王海亮

（陆军工程大学石家庄校区，石家庄 050003）

捷联惯导系统（SINS）具有输出导航参数多、完全自主、隐蔽性强等突出优点，因此被广泛应用于陆基导弹、武器发射车等陆地导航系统中。但是其误差随时间积累[1-2]，不利于长时间的高精度导航，因此组合导航技术得到了国内外学者的广泛关注。

全球卫星定位系统（GPS）导航范围广、精度高，成为组合导航技术的首选，但是其容易发生信号遮挡，具有暴露位置等缺点，而里程计（OD）通过输出位置增量，借助航位推算（DR）方法能够实现自主导航，并且与INS组合导航误差比惯导系统导航误差小，所以 SINS/DR组合导航技术在车辆导航领域有着重要意义[3-5]。然而里程计与捷联惯导安装在车体的不同位置，存在安装偏差角，并且里程计的标度因数受到车辆载荷、轮胎磨损、气压和温度等因素的影响[6]，因此对里程计的安装偏差角以及标度因数进行标定有利于提高SINS/DR组合导航的精度。目前针对里程计的标定方法主要有离线标定和在线标定[7]。离线标定的方法是通过确定车辆行驶直线路径的起点终点进行里程计的参数辨识，该方法对车辆行驶路径要求较高。文献[8]采用零速修正的惯导信息进行里程计标定，但是需要间隔一定时间停车一次，降低了车辆的机动性。文献[9]基于车辆的运动约束，通过卡尔曼滤波进行里程计标度因数误差的最优估计，但是文章没有考虑里程计与捷联惯性组的安装误差角。文献[10-11]通过建立航位推算的误差模型，利用卡尔曼滤波方法进行里程计参数的在线辨识，取得了较好的效果。文献[12]采用EKF进行里程计参数辨识，提高了系统的鲁棒性。文献[13]对里程计标度因数误差、杆臂误差进行了建模补偿，提高了INS/OD的组合导航精度。本文提出利用运动学非完整约束算法进行里程计参数的在线辨识。

1 SINS/DR组合导航系统误差分析

选取东北天为导航坐标系，记为n系；里程计坐标系与车体坐标系重合，记为m系，y轴沿车体纵轴指向正前方，x轴沿车体横轴方向指向右方，z轴与x轴、y轴构成右手直角坐标系；惯导坐标系记为b系。通常在安装惯性组件时会尽可能使b系与m系重合，但是受到安装工艺的限制，m系与b系之间存在着安装误差角，即为里程计安装偏差角依次为航向安装偏差角误差、横滚安装偏差角误差和俯仰安装偏差角误差。

1.1 里程计标度因数误差分析

里程计的输出是脉冲信号，车轮每旋转一周，里程计输出c个脉冲，此时车辆行驶距离为L，则里程计输出脉冲与车辆行驶距离之间存在如下关系：

由式(1)可以看出，里程计推算距离的精度很大程度取决于标度因数KD的稳定性。然而标度因数受到车轮充气程度、车轮磨损、车辆载荷、行驶中轮胎打滑等因素的影响，为了能够获得车辆行驶的精确里程或速度，必须要对里程计的标度因数进行标定，从而减小标度因数误差对导航精度的影响。基于里程计的工作原理，在不考虑车辆发生侧滑和跳跃的情况下通过记录行驶距离为L的时间，即可求解车辆的行驶速度里程计输出速度在车体坐标系的投影为：

车辆真实速度在导航坐标系的投影为：

1.2 航位推算误差模型

由于惯导坐标系与里程计坐标系之间存在安装偏差角，则惯导坐标系到里程计坐标系的转换矩阵可以表示为：

则里程计输出在惯导坐标系的投影为：

由式(7)可以看出，由于里程计坐标系与惯导坐标系存在小角度安装偏差，导致里程计的输出在惯导坐标系上的投影存在x、z轴的分量，并且与横滚安装偏差无关。假设方位安装角与俯仰安装角的误差分别为均满足小角度要求，所以同理。忽略二阶小量，则里程计的实际输出在惯导坐标系的投影为：

则式(8)进一步化简为：

因为M1中含有小量，所以忽略二阶小量得：

由于a为小角度，所以公式(11)中M1可简化为

综上，里程计方位安装角误差以及俯仰安装角误差对速度解算存在较大影响，因此需要考虑安装误差，以提高SINS/DR组合导航系统的导航精度。

由于里程计输出速度在导航系的投影为

对式(12)求导，并结合式(11)得：

1.3 捷联惯导误差模型

按照文献[9-11]列写捷联惯导的误差方程如下：

2 滤波算法

2.1 状态方程

陀螺、加计的误差由零偏以及随机误差组成，其中零偏为随机常数，随机误差为均值为0的白噪声，并认为里程计与惯性元件之间的安装误差经过上电后保持为一常数不变，则有如下关系：根据式(14)～(18)可以得到系统状态方程为：

式中，F为状态转移矩阵，G为噪声驱动矩阵，W为系统噪声矩阵。

2.2 基于车辆运动学非完整约束单点算法的观测量设计

利用里程计的输出求解车辆速度信息并将其转化为导航系的速度矢量，与捷联惯导输出的速度矢量进行比较，两者的差值作为系统的量测量之一，如下：

车辆在低速转向运动时，车体的横向加速度较小，轮胎不会发生侧滑，该时刻车辆的转向运动可用阿克曼转向模型来描述。根据阿克曼转向原理，车辆转向时，存在一点使得四个车轮均绕其做圆周运动。如图1所示，假设车辆在很短的时间内由A点移动到B点，移动距离dS可以通过里程计获得，行驶方向变化的角度为为车辆的旋转半径，当车辆直线运动时，可以认为

图1 车辆转弯运动分析Fig.1 Analysis of vehicle turning motion

向心加速度以及车辆旋转角速度的观测值可以通过惯导输出获得，将其换算到载体坐标系如下：

由于车辆线运动相对于地球的旋转角速度相对较小，所以忽略其影响，得到：

根据式(25)(26)可得向心加速度差值的观测值为：

向心加速度差值误差量的误差模型推导如式(31)～(35)所示。

对式(24)进行全微分可得：

由式(13)及(32)～(36)可以得到量测矩阵为：

式(36)中，V表示量测噪声矩阵。按照如上设计的状态方程、量测方程进行卡尔曼滤波，完成车载里程计参数的在线标定。

3 仿真试验与车载试验验证

为了验证所提方法的可行性，本文按照真实车辆的行驶规律，设计了车辆的加速、匀速、左转、右转、爬升、下降、最后减速为零的运动形式，模拟了车辆的行驶环境，进行仿真分析。车辆的具体行驶路径为：①静止100 s；②沿正北方向以1 m/s2的加速度行驶10 s；③匀速直线行驶110 s；④以2 (°)/s的角速度左转90°（45 s），之后匀速直线行驶100 s；⑤以9 (°)/s的角速度右转450°（50 s），匀速直线行驶100 s；⑥以2 (°)/s的俯仰角速度爬升10 s，之后匀速行驶50 s，之后再以−2 (°)/s的俯仰角速度行驶10 s，完成车辆的爬坡运动，车辆恢复水平；⑦匀速直线运行100 s；⑧以-2 (°)/s的俯仰角速度行驶10 s，并匀速行驶50 s，之后以2 (°)/s的俯仰角速度行驶10 s，完成车辆的下坡运动，从而车辆再次恢复水平；⑨匀速直线行驶100 s；⑩以−2 m/s2的加速度做减速运动5 s，车辆恢复静止100 s。

设定车辆行驶的初始位置：经度为108.909°E，纬度为34.246°N，海拔高为380 m，车辆的初始速度为0。得到车辆的行驶轨迹如图2所示，车辆行驶至东经108.904°附近绕行450°，旋转一周后向北行驶。

图2 车辆的行驶轨迹Fig.2 Track of vehicle

图3 车辆的行驶轨迹二维平面图Fig.3 Two-dimensional map of vehicle track

车辆行驶轨迹的二维平面图如图3所示。设置惯性元件的参数如下：陀螺仪零漂为0.01 (°)/h，陀螺随机游走为加速度计常值漂移为加计随机游走为设置车辆的初始速度为零，方位角、横滚角、俯仰角均为零；姿态误差角为为了方便从仿真结果看出应用算法的效果，这里将里程计与惯导之间的安装偏差角设置得稍大一些，航向安装偏差角为150¢，俯仰安装偏差为100¢；里程计的刻度因数误差为 1%。当单纯使用航位推算进行车辆轨迹求解时，得到如图4所示行驶路径，可见单纯使用航位推算会产生较大的导航误差。

利用SINS/DR组合导航方式进行车辆导航，并按照以速度差作为观测量，通过卡尔曼滤波的方式进行里程计的标定（记为滤波1）；按照基于运动学非完整约束算法设计的观测量进行滤波，标定里程计参数（记为滤波2）。图5给出了利用加速度计与里程计得到的向心加速度的对比结果。

车辆左转、右转时的行驶速度为10 m/s，左转时角速度为因此左转时车辆的向心加速度为同理，车辆右转时角速度为9 (°)/s，因此右转时车辆的向心加速度为，以上计算结果与图5中车辆向心加速度仿真结果基本吻合，证明了仿真结果的正确性。

图4 航位推算系统轨迹与真实轨迹的对比Fig.4 Comparison between the real track and the track of dead reckoning system

图6～7给出了两种滤波方式下，里程计航向安装偏差角误差以及标度因数误差的估计残差的对比结果。从图中仿真结果可见，第二种滤波方式能够实现里程计航向安装偏差角误差以及标度因数误差的最优估计。

图6 两种滤波方式下里程计安装偏差角的估计残差Fig.6 Comparison on residuals of installation deviation angle error estimation between the two filters

图7 两种滤波方式下里程计刻度因数的估计残差Fig.7 Comparison on res iduals of scalefactor estimatio n between the two filters

对于车载导航系统，由式(11)可知里程计的航向安装偏差角以及标度因数误差对车辆水平轴向速度影响较大，即对导航精度影响较大。由于滤波2相比滤波1对里程计的航向安装偏差角误差以及标度因数误差进行了最优估计，因此，由图8可见第二种滤波方式下经纬度误差明显较小，实现了较高精度的导航。当车辆行驶960s，对两次滤波进行组合导航误差分析，采用滤波2的组合导航方式造成的经度误差为−1.098×10-4(°)，采用滤波1的组合导航方式造成的经度误差为−3.231×10-4(°)，即东向位置误差提高了19.6 m。同理采用滤波2的组合导航方式造成的纬度误差为−1.257×10-4(°)，采用滤波1的组合导航方式造成的纬度误差为−2.531×10-4(°)，即北向位置精度提高14.2m。与采用滤波1进行组合导航相比，由于滤波2进行组合导航时，标度因数估计精度有所提高，所以高度误差也稍有减小，但两种组合导航方式对车辆的高度精度整体相差不大。

图8 两种滤波方式下组合导航系统的位置误差对比结果Fig.8 Comparison o f position error estimation between the two filters

为了验证所提方法的可行性，在车辆的航向角速度中加入均值为零的白噪声，模拟车辆的随机轻微转向运动，使车辆的模拟路径接近真实路径，并利用两种滤波方式进行里程计的在线标定，得到两种滤波方式下组合导航的行驶轨迹对比结果，如图9所示。可见该方法能够较高精度的辨识里程计参数，实现较高精度的组合导航。

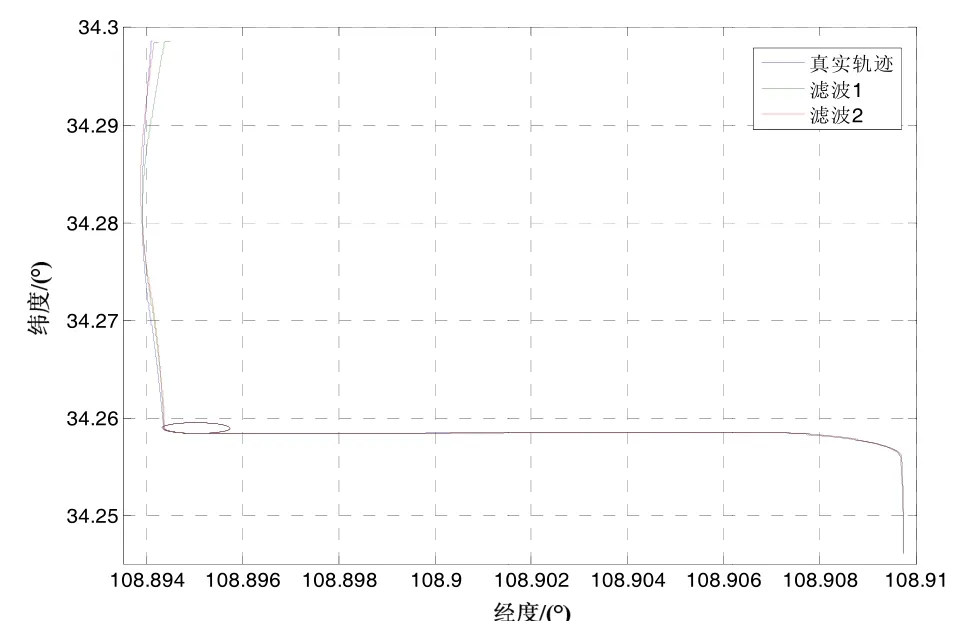
图9 两种滤波方式在模拟真实路径下导航轨迹对比结果Fig .9 Navigatioon path comparriison results betw een the two filteers in simulatedd real trajectory

为了验证本文所述方法的可行性，设计跑车试验，试验中所用设备的相关参数如下：陀螺零偏稳定性≤0.02(°)/h，随机游走系数加速度计零偏；里程计标度因数误差≤0.5%；跑车利用高精度 GGPS位置信息作为航位推算的位置参考，GPS定位精度≤10 m (1σ)。实车试验装置如图10所示。里程计安装于非转向轮的轮轴上。高精度惯导以及GPS安装如图10所示。

利用已知车辆行驶平直路径起点终点位置的传统里程计标定方式，对里程计参数进行标定，得到里程计刻度因数为0.0885m/pulse，里程计的定位精度为行驶里程）；航向安装偏差角为 0.20°，俯仰安装偏差角为 0.41°。试验中，车辆的行驶路径如图11所示。

图10 试验装置Fig .10 Experimental device

在实车试验中，初始装订里程计的标度因数为0.085m/pulse，航向安装偏差角以及俯仰安装偏差角均为0。按照上述里程计参数辨识方法进行里程计参数的在线辨识，得到车载试验的误差参数如图12所示。从图12可见，里程计的标度因数误差约为5‰，所提方法的标定结果与里程计传统标定结果基本吻合。利用本文方法得到航向安装偏差角为 0.1964°，俯仰安装偏差角为 0.4134°，从而验证了里程计参数在线辨识方法的可行性。

图11 车载试验跑车路径Fig.11 Path graph of vehicular experiment

图12 车载试验在线标定结果Fig.12 Online calibration results of vehicular experiment

4 结 论

针对里程计标度因数误差以及安装偏差角误差对SINS/DR组合导航精度影响较大的问题，本文提出了一种基于运动学非完整约束的里程计参数在线辨识方法，通过分析安装偏差以及标度因数误差对里程计输出的影响，建立航位推算的误差模型。将里程计安装偏差以及标度因数误差作为状态量，建立卡尔曼滤波状态方程，通过里程计输出速度解算得到车辆的向心加速度与捷联惯导加速度计的输出计算得到的向心加速度做差作为量测之一；将捷联惯导与里程计输出速度做差作为量测之二，建立卡尔曼滤波量测方程，进行里程计参数在线辨识；最后通过理想路径和模拟真实路径的仿真以及实车试验，发现该方法能够提高里程计航向安装偏差角以及标度因数误差的估计精度，从而实现较高精度的车辆导航。