螺旋线对斜拉桥斜拉索高雷诺数风致振动影响的试验研究

刘庆宽， 卢照亮， 田凯强， 胡 波， 马文勇

(1.石家庄铁道大学 大型结构健康诊断与控制研究所，石家庄 050043；2.河北省大型结构健康诊断与控制重点实验室，石家庄 050043; 3. 石家庄铁道大学 土木工程学院，石家庄 050043; 4. 石家庄铁道大学 工程力学系，石家庄 050043)

自日本明港西大桥的斜拉索被观测到风雨振现象[1]以来，世界上多座大桥都有过这方面的报道，如美国的Fred Hartman桥[2]、日本的Sun Bridge桥[3]、我国的杨浦大桥[4]等也都发生过风雨激振现象。因为其振幅大、危害严重，吸引了很多学者针对其机理和控制措施进行了研究。在机理方面，认为在特定的风速和风向下斜拉索表面形成的水线是导致风雨振发生的关键因素之一。在振动控制的气动措施方面，以阻碍和防止水线形成为目标，在斜拉索表面设置凹坑，或者缠绕螺旋线是常用的方法，其中缠绕螺旋线的方法应用更广泛一些。顾明等[5]研究结果表明，若缠绕螺旋线直径太小，斜拉索振幅会增大；Zasso等[6]研究表明，螺旋线减弱了漩涡脱落的轴向相关性；李寿英等[7]的研究表明，螺旋线使斜拉索漩涡脱落强度大大降低；刘庆宽等[8]分别改变螺旋线的直径和缠绕间距，研究了具有抑制风雨振效果的螺旋线参数组合。

在风雨振的研究过程中，研究者发现在没有降雨，或者降雨已经停止的情况下仍然观测到了大幅振动，被命名为干索驰振。Flamand[9]、Zuo[10]、Matsumoto[11]等都对这些振动现象进行了报导，Cheng[12]、Benidir[13]、Piccardo[14]、Nikitas[15]等针对该振动现象进行了机理研究，认为临界雷诺数时特殊的气动力和流场，是导致干索驰振的重要因素。刘庆宽等[16-17]研究了各种螺旋线参数组合情况下高雷诺数区域斜拉索的气动力，并研究了斜拉索表面粗糙度改变时高雷诺数下气动力的变化规律，发现无论是缠绕螺旋线，还是表面粗糙度的变化，在远高于风雨振发生的高雷诺数区域，斜拉索的气动力会有特殊的变化规律。针对干索驰振问题，缠绕螺旋线的斜拉索能够抑制风雨振，但是在高雷诺数区域气动稳定性如何，是值得关注，也是桥梁设计人员所关心的问题。

本研究针对缠绕螺旋线的斜拉索，通过风洞试验研究了高雷诺数时的振动特性，为相关的研究和设计提供参考。

1 风洞试验

本试验在石家庄铁道大学风工程研究中心的STU-1风洞内进行，该风洞是一座单回路双试验段回/直流大气边界层风洞，其高速试验段宽2.2 m，高2.0 m，长5 m，最大风速80 m/s。

模型的材质为有机玻璃管，直径D=120.13 mm，该直径是分别在模型的五个断面、每个断面四个方向测试结果的平均值，多处测试是为了确认模型无变形。

模型长度L=1 700 mm，此长度是为了保证模型处于风洞两侧洞壁形成的边界层之外的均匀稳定的流场中。模型区在40 m/s和65 m/s时的湍流度不大于0.16%[18]，如图1所示。

斜拉索模型两端设置端板，以保证模型周围流场的二维流动特性。模型中心的钢管贯穿到风洞的洞壁外，通过弹簧悬挂在机构上，通过弹簧连接的力传感器测试斜拉索模型振动时的动态力，并根据标定关系换算成振动的位移时程。

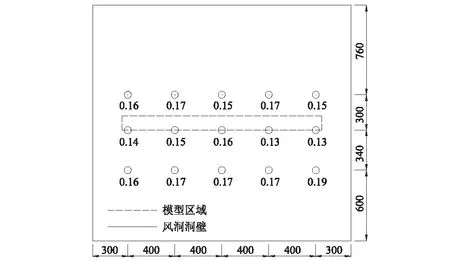
图1 模型区湍流度(尺寸单位：mm；湍流度单位：%)Fig.1 Turbulence intensity in model area (dimension unit: mm; turbulence intensity unit: %)

模型系统的自振频率f=2.48 Hz，各模型的Sc数(Sc=4 πmξ/ρD2，其中m为模型单位长度质量，ξ为阻尼比，本试验阻尼比为0.78%，ρ为空气密度，D为模型直径)在8.3～8.9之间，试验系统的Sc值比实际斜拉索的值要小，此设计一是为了得到相对安全的结果，二是在较容易振动的情况下研究相关参数对振动的影响。斜拉索模型安装如图2所示。

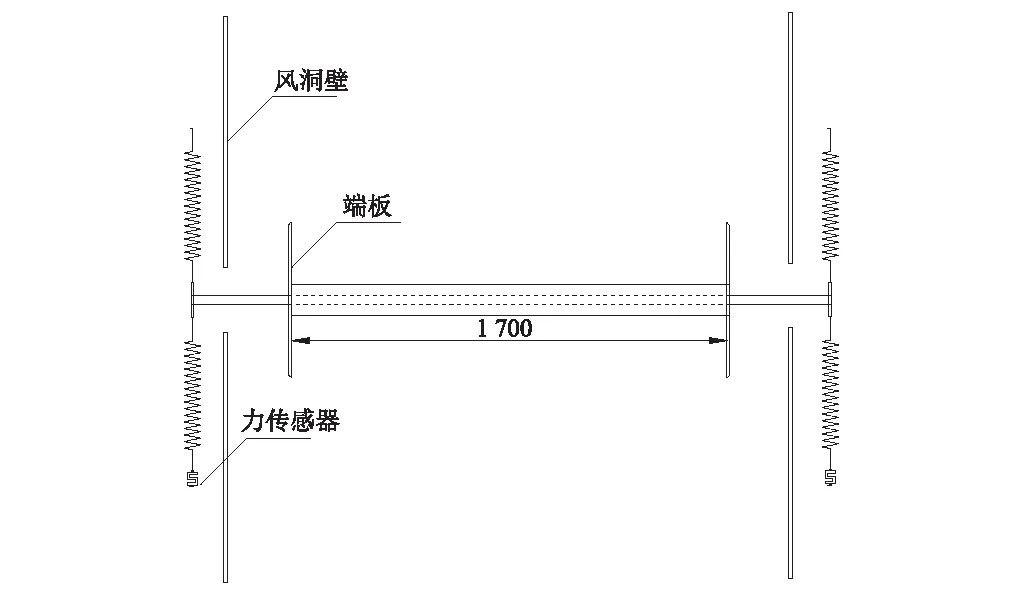
图2 斜拉索模型安装图(mm)Fig.2 Model installation diagram of the cable(mm)

斜拉索模型表面缠绕的螺旋线直径d采用0.89 mm、1.24 mm、1.71 mm、1.84 mm、2.35 mm五种，缠绕间距S分别为6D、8D、10D、12D、14D五种，其中D为斜拉索直径，均为双螺旋线缠绕，即每个断面上都有两条螺旋线，其连线经过断面的圆心。

试验过程中记录洞体内空气的温度、湿度和气压，进行空气动粘性系数的修正，并结合斜拉索模型直径和来流风速，计算得到试验的雷诺数。试验的雷诺数考虑了在临界雷诺数区域的加密，具体数值如表1所示。

表1 试验雷诺数范围及步长

为了叙述方便，将试验工况进行编号，螺旋线间距6D、8D、10D、12D、14D对应的工况分别用6、8、10、12、14表示，螺旋线直径0.89 mm、1.24 mm、1.71 mm、1.84 mm、2.35 mm对应的工况分别用1、2、3、4、5表示，如工况14-1表示缠绕间距为14D、螺旋线直径为0.89 mm的工况。工况组1表示螺旋线直径为0.89 mm时五种缠绕间距的工况组，工况组6表示6倍缠绕间距时五种螺旋线直径的工况组。各个试验工况编号如表2所示。

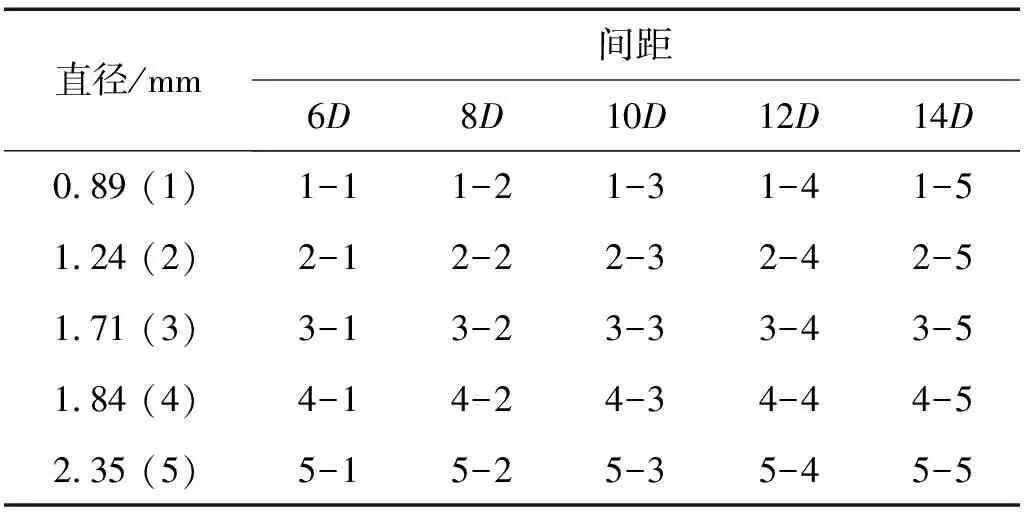
表2 试验工况组编号表

2 螺旋线参数对斜拉索振幅的影响

2.1 螺旋线缠绕间距对斜拉索振幅的影响

保持螺旋线直径d不变，改变螺旋线的缠绕间距S，得到斜拉索振幅随雷诺数的变化情况，如图3所示。

图3显示了工况组1五种缠绕间距下斜拉索振幅随雷诺数变化情况，由图3可得：第一，没有缠绕螺旋线的模型，在33万～37.5万雷诺数范围内出现较大振幅的振动，随着螺旋线间距的增加，斜拉索振幅大致呈现递增的规律，说明同等螺旋线直径下，减小螺旋线的间距，可以减弱斜拉索在高雷诺数下振动。第二，同没有螺旋线的模型相比，缠绕螺旋线模型的起振风速相对较大，说明斜拉索表面缠绕螺旋线可以提高起振风速。第三，随着螺旋线间距的增大，在较短的雷诺数变化范围内，即可发生从不振动到大幅振动的变化，而小间距时，振幅是随着雷诺数的增大缓慢增长的。工况组2～工况组5，总体规律类似，不再赘述。

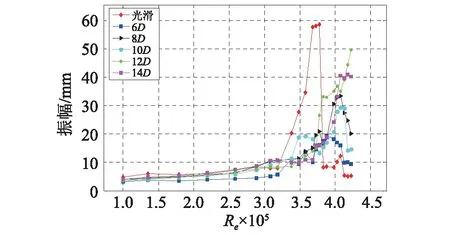
图3 五种缠绕间距下振幅随雷诺数变化情况Fig.3 The relationship between vibration amplitudes and Reynolds number of five helical line winding spacing cable models

将试验每个工况下振幅最大值选出，相同螺旋线直径的五个工况按缠绕间距从小到大相邻摆放，得到每种螺旋线直径下各螺旋线缠绕间距的最大振幅，如图4所示。从图中可以发现：①相同螺旋线直径下，随着螺旋线间距的增加，模型最大振幅整体规律上呈增大的趋势；②14D螺旋线缠绕间距下，个别工况下最大振幅比光滑模型振幅大。

图4 25种工况下振幅的最大值Fig.4 The maximum amplitude of the 25 kinds of operating conditions

将每种螺旋线间距下不同螺旋线直径的斜拉索模型的最大振幅选出，作为该种间距下的最大振幅，并进行相互比较，如图5所示。从图中可以发现：随着螺旋线缠绕间距的增加，每种缠绕间距下的最大振幅增加。

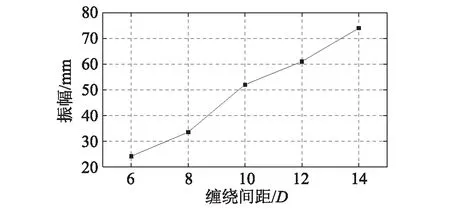
图5 各缠绕间距下振幅最大值比较图Fig.5 The comparison chart about maximum amplitudes in each helical line winding spacing

2.2 螺旋线直径对斜拉索振幅的影响

保持螺旋线缠绕间距为10D，对比相同螺旋线缠绕间距下不同螺旋线直径的斜拉索振幅，如图6所示。可以发现：相同缠绕间距、不同螺旋线直径下，振幅与螺旋线直径并不是简单的线性关系，振幅的最大值并没有产生在螺旋线直径最小的工况下，而随着螺旋线直径的增加整体的抑振效果也并没有增加，此工况下振幅的最大值出现在直径为1.71 mm的螺旋线直径工况下，但是与改变缠绕间距相比，各个螺旋线直径下的振幅差距并不明显。但就整体规律而言，螺旋线直径越大模型的起振风速越提前。其余工况组总体规律类似，不再赘述。

将试验每个工况下振幅最大值选出，相同螺旋线缠绕间距的五个工况按螺旋线直径从小到大排列，得到每种螺旋线间距下各螺旋线直径的模型振幅，如图7所示。从图中可以发现：相同螺旋线间距下，最大振幅与螺旋线直径并不是简单的线性关系，且螺旋线间距越大，线性关系越不明显。

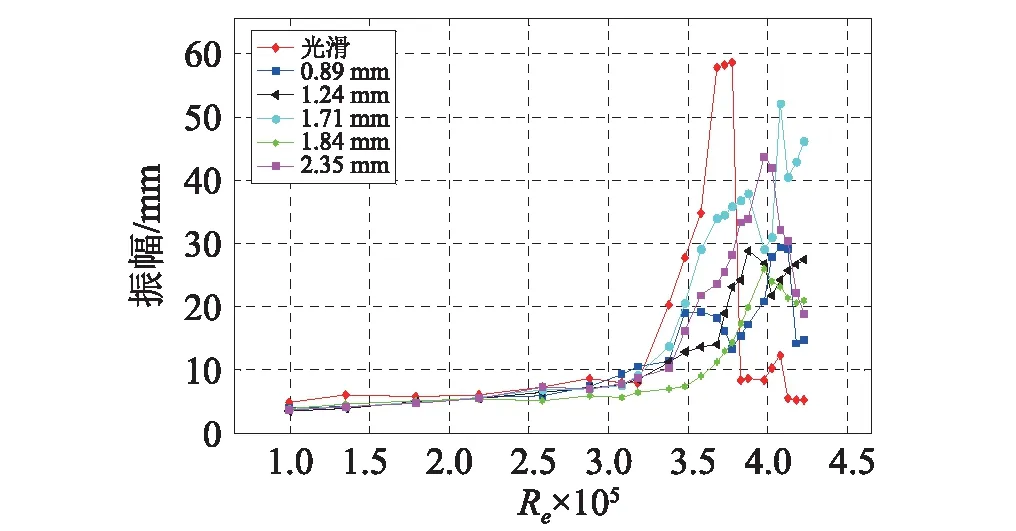
图6 五种螺旋线直径下振幅随雷诺数变化情况Fig. 6 The relationship between vibration amplitudes and Reynolds number of five helical line diameter cable models

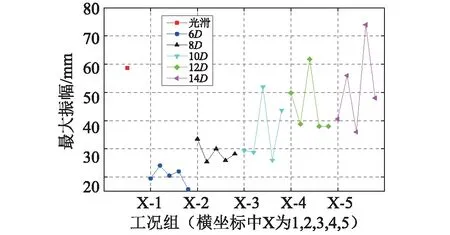
图7 每种螺旋线间距下螺旋线直径与最大振幅关系图Fig.7 The relationship betweenmaximum amplitude and helical line diameter in each winding spacing

将每种螺旋线直径下不同螺旋线间距的斜拉索模型的最大振幅选出，作为该种螺旋线直径下的最大振幅，并进行相互比较，如图8所示。从图中可以发现：振幅最大值随着螺旋线直径的增加呈先增大后减小的趋势。

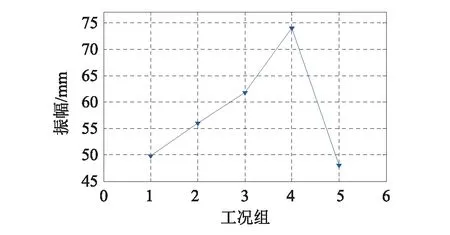
图8 各螺旋线直径下振幅最大值比较图Fig. 8 The comparison chart about maximum amplitudes at different helical line diameter

3 螺旋线参数对斜拉索振动稳定性的影响

由于在高雷诺数区域的振动通常不是振幅十分稳定的振动，为了分析振动的稳定性，将振动时程中的振幅提取出来，并分析其RMS值，工况组5模型振幅的RMS值如图9所示。与无螺旋线斜拉索相比，缠绕螺旋线模型的振幅稳定程度有所提高，随着螺旋线间距的增加，RMS的峰值增大，说明振动的稳定性变差。

图9 工况组5五种螺旋线间距下的振幅RMSFig.9 The RMS of amplitude of five winding spacing cable models for working group 5

将试验所有工况的RMS值随雷诺数的变化规律按照相同间距放在一起的方式进行摆放，如图10所示。0的位置表示无螺旋线的斜拉索的情况。通过比较得到每种缠绕间距下振幅RMS最大值，并用实线加粗。通过比较可知：随着螺旋线间距的增加，每种螺旋线缠绕间距下振幅RMS值最大值增大。

图10 各螺旋线间距下振幅RMS最大值比较图Fig.10 The comparison chart about maximum RMS of amplitudes in each winding spacings

4 结 论

本文通过对直径为120.13 mm的斜拉索模型分别缠绕25种螺旋线的振动情况进行了风洞试验，并分析了各工况下斜拉索振幅和各工况组最大振幅随雷诺数的变化规律，得到以下结论：

(1)螺旋线直径一定时，缠绕间距越大，高雷诺数下模型最大振幅越大；

(2)缠绕间距一定时，高雷诺数下螺旋线直径与最大振幅并不呈简单的线性关系；

(3)螺旋线间距的减小，能提高振动的稳定性。