基于智能手机的行人荷载测试研究
2018-08-02潘子叶
潘子叶, 陈 隽, 谭 寰
(同济大学 土木工程防灾国家重点实验室,上海 200092)
建筑物中行人、观众或住户的行走、跳跃、屈伸或跑动等动作对支撑结构的动力作用称为人致荷载,由其引起的结构振动称为人致结构振动。这其中,屈伸(bounce)指双脚不离开地面、身体重心的上下运动,常见于演唱会和体育比赛的观众欢庆方式。对于人行桥、室内连廊、悬臂体育看台、大跨度楼盖以及长柔楼梯等结构,过大的振幅会引起建筑物中使用者的不舒适感觉甚至恐慌,导致结构振动舒适度问题。近年来,随着上述大跨度柔性结构的大量兴建,人致结构振动舒适度问题越来越受到设计人员以及研究者的重视[1-4]。
人致荷载的动力特性与取值是人致结构振动分析的核心问题,建立可靠的荷载模型需要大量的实测数据。人致荷载主要有直接测试和间接测试两种方法。直接法中,陈隽等[5]采用固定测力板、测力鞋垫、孙利民等采用测力跑步机等仪器获得荷载时程。测力板精度高但数量有限,往往只能获得有限步荷载时程。测力跑步机由于测试者的运动受到跑步机履带速度的控制,所获得的荷载参数的变异性较正常地面上偏小,测试结果的代表性还存有争议。测力鞋垫虽然可以获得连续荷载时程,但由于测试中鞋垫始终与测试者的足底有接触,与实际存在的腾空状态(如步行时的单腿摆动、跳跃时的腾空等)不符,测试值需要进行后处理。此外,以上三种测试仪器主要针对单人情况,目前还难以实现人群荷载的测试。间接法是通过测试其他物理量间接获得人致荷载。例如,由录像方式获得行人运动时的特征参数;由结构响应反演获得外部荷载;或者由人体运动重心的加速度计算人致荷载等。近年来,间接法测试由于过程简单、容易实现人群荷载的测试而受到重视。总体上,如何在测试者“自然活动”的状态下完成荷载的连续测试,并且能推广到人群情况,是人致荷载试验研究中的关键技术问题。
当前,以智能手机为代表的各种智能携带设备,正在以惊人的速度和程度影响并改变着现代人的生活和工作方式。伴随着硬件技术的持续创新以及性能指标的迅速提升,智能手机的综合功能日益强大。其中,建立在微机电系统技术上的三轴加速度传感器、和陀螺仪传感器等内置传感器,可记录手机的加速度及其方向,并已用于工程结构的振动测试[6-7]。智能手机的这些新功能为解决人致荷载测试的技术难题提供了全新的思路和途径。据我国工信部2015年12月底的统计数字,我国手机用户已达到13.06亿户,普及率为每百人95.5部。作为人们日常生活中必不可少的工具,将手机和其使用者相结合来实现行人荷载测试,势必为建筑结构活荷载的试验研究提供新手段。
基于上述认识,本文首先通过振动台和三维动作捕捉试验检验智能手机的测试精度,完成了设备的软硬件选型,在此基础上开展了智能手机对人体运动状态以及行人荷载的实测,实测结果与固定测力板结果的对比,证明了手机测试人致荷载的可行性。
1 智能手机加速度测试与坐标转换
图1所示为一般智能手机的测试坐标系系统(局部坐标),x,y,z坐标轴以及转动的正方向,直线箭头指向为加速度数据的正方向,三轴两两垂直且x,y轴所构成的平面与手机屏幕平面平行。内置三轴加速度传感器可以记录手机在x,y,z方向上的加速度值,三轴陀螺仪可以记录手机绕三个坐标轴转动时的角速度ϑx, ϑy, ϑz。这里,陀螺仪传感器的正方向符合右手法则,即拇指指向加速度传感器正方向时,四指弯曲的指向为角速度正方向(图1中旋转箭头所示)。
与普通传感器的使用过程相同,利用手机测试时,需要将手机固定于被测物体上,确保不发生相对滑移,并使手机的某一轴线与振动方向一致,则此轴线上的实测值可作为被测物体此处的加速度。此外,利用携带手机进行人体运动状态的测试时,手机局部坐标系方向会随人体运动而不断发生变化。因此必须对手机原始测试结果进行坐标转换,以转换为相对于某一固定方向(如垂直于地面方向的大地坐标系)的实测值。

图1 手机局部坐标系与初始对中装置Fig.1 Smartphone’s local coordinate and centering device
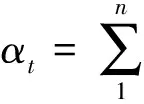
(1)
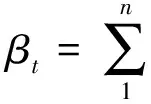
(2)
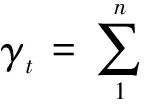
(3)
式中:n为直到t时刻的总采样点个数,即n=t/Δt,Δt为采样间隔。
手机的上述空间转动可以等价为按照某一顺序依次绕三个坐标轴的转动,三个相对转角(进动角、章动角和自旋角)统称为欧拉角,常用以描述刚体在三维欧几里得空间的取向。因此,手机在t时刻的轴线方向可通过三个基本旋转矩阵获得。以图2所示的先z轴,再x轴,最后y轴的旋转顺序为例,每步对应的旋转矩阵为式(4)~(6)。
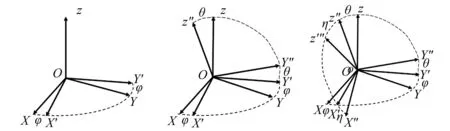
图2 手机坐标轴转换示意图Fig.2 The rotation of local coordinate
(4)
(5)
(6)

[ax,ay,az]T=H[a1,a2,a3]T
(7)
(8)
式(7)中,H为坐标转换矩阵,上标T表示转置。
2 测试系统选型与精度检验
本节利用小型振动台设备开展了不同手机与不同数据采集软件的性能试验,通过手机测试信号与振动台实际输出信号的对比,完成了手机测试系统的软硬件选型,并对选定测试系统的测试精度进行了多种信号的检验。
2.1 测试系统软硬件选型
根据市场占有率和传感器配置,首先筛选出6部常用的智能手机,主要信息如下表1所示。

表1 手机的软硬件配置信息
从市场占有率、传感器标称性能、对应软件性能以及是否免费等几个方面综合考虑,本文最终采用了多种不同型号的iPhone系列手机进行振动台标定。
图3所示为振动台验证试验。1号装置是有机玻璃板,通过螺丝(2号)固定于Quanser振动台上;手机卡入固定在有机玻璃板上的手机壳中(3号)。固定手机时,保证手机的x轴在试验过程中与振动方向保持一致,且与有机玻璃板不发生滑移。

图3 振动台验证的安装照片Fig.3 Verification test by shaking table
此外,为了验证多向振动对各个坐标轴采集数据的精度是否造成影响,有试验工况将有机玻璃板逆时针旋转45°后固定于振动台台面上(x轴和y轴共同参与振动),如图4所示。

图4 振动台验证的安装照片(45度固定)Fig.4 Verification test by shaking table(45 degree fixed)
2.2 测试精度检验:正弦波
人致荷载是一种周期性荷载,为检验选定的测试系统对于周期信号的测试精度,试验中振动台输入了7条正弦波,频率1.2 ~ 3.4 Hz之间,覆盖了人致荷载的主要频率范围。图5和图6比较了1.6 Hz和3.4 Hz两种工况下手机实测加速度与振动台输入加速度的时程曲线和傅里叶幅值谱。对比表明,手机测试值与振动台输入信号的时程曲线和幅值谱非常接近,其他测试工况结果与此类似。在低频(1.6 Hz)、中频(2.4 Hz)、高频(3.4 Hz)三种工况下,手机测试值与振动台输入的平均峰值误差为3.1%,2.2%和3.0%,手机测试信号幅值谱主频与输入信号主频完全一致。这里平均峰值误差指两条曲线所有对应峰值误差的平均值。其他工况的结果相似:峰值误差在3.5%以内,而主频值则几乎完全一致。
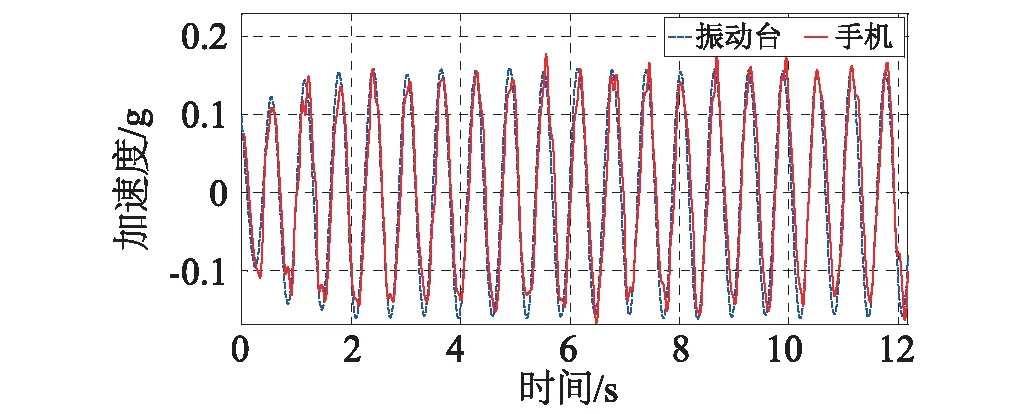
(a)时程对比
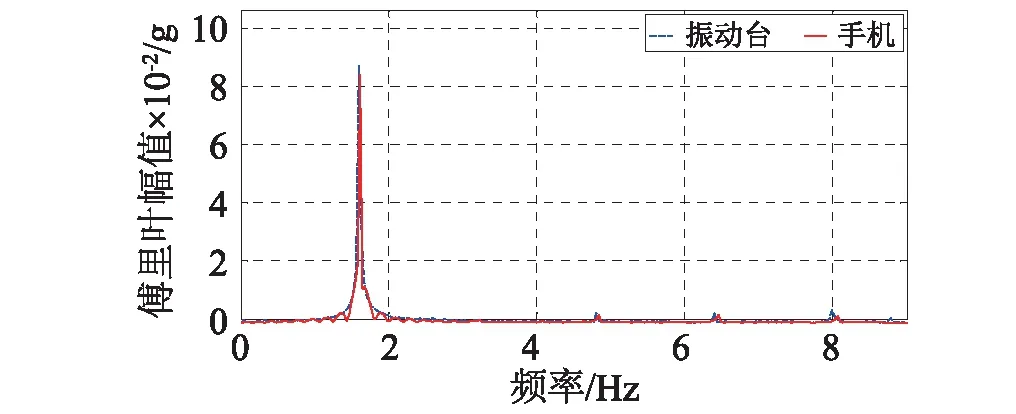
(b)幅值谱对比图5 1.6 Hz正弦加速度输入的测试精度对比Fig.5 Comparisons for test case of 1.6 Hz sine wave input

(a)时程对比
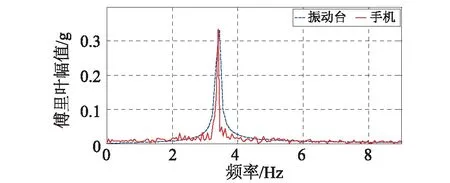
(b)幅值谱对比图6 3.4 Hz正弦加速度输入的测试精度对比Fig.6 Comparisons for test case of 3.4 Hz sine wave input
2.3 测试精度检验:正弦扫频信号
试验中输入了多组变幅正弦扫频信号(1.2~3.6 Hz),其中一组扫频信号的时域和频域对比结果见图7。为方便对比,图中还比较了两条曲线的1 s移动均方根值(1s Running Root-Mean-Square, 1sRMS)。图7中两条1sRMS曲线点对点的平均误差为18.88%,而频域特征几乎一致。试验结果表明,手机对于扫频信号时域幅值的测试精度一般,对信号频域特征的测试精度高。
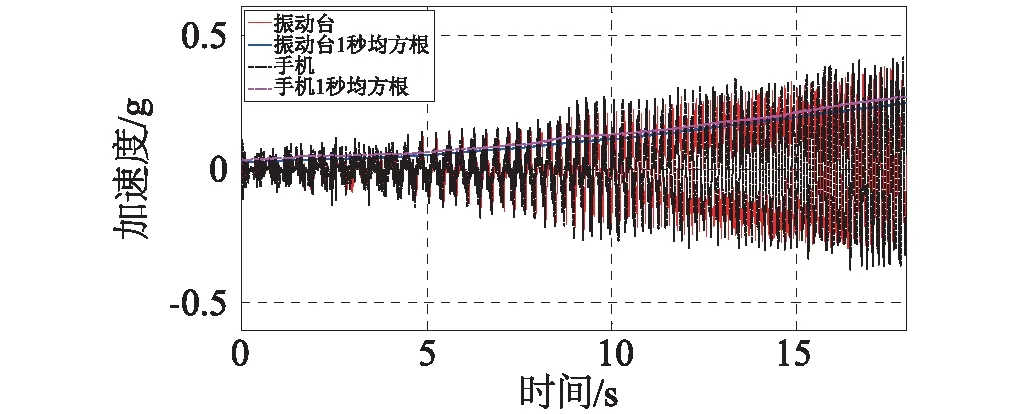
(a)时程对比

(b)幅值谱对比图7 扫频波输入工况比较Fig.7 The comparison of shaking table data and smart phone sensor data under sinusoidal vibration
2.4 测试精度检验:地震动信号
为了验证手机测量复杂振动信号的精度,还进行了四种地震波输入的试验:EL-Centro、Northbridge、Kobe和Mendocino地震波。图 8、图9所示为不同型号手机记录值与EL-Centro地震波的比较。iPhone5C及以上手机的信号可以反映输入地震波的宏观时域特征(如波形、峰值数量等),但在信号的细节特征上仍有差距,此外幅值谱的特性也有不同。其他三个地震波试验的结果类似。由于不同手机的加速度传感器类型不同,上述试验结果表明,现阶段应慎重采用手机进行地震动等时域特性复杂信号的直接测试。
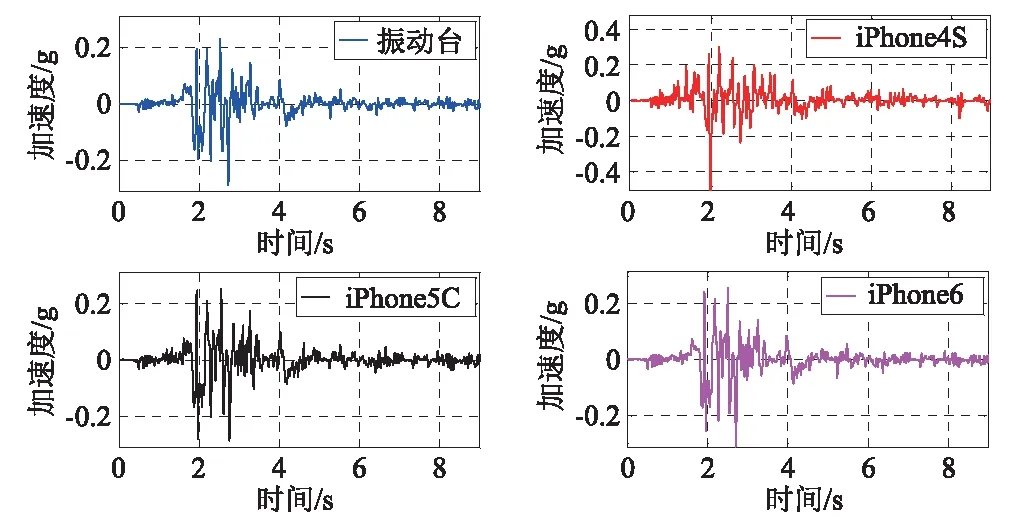
图8 振动台输入El-Centro地震波加速度数据与不同型号手机加速度传感器记录对比Fig.8 The comparison of the recording time history under El-Centro earthquake vibration between shaking table and smart phones with different types

图9 四种不同型号手机与振动台输入El-Centro地震波加速度数据的傅里叶幅值谱对比Fig.9 The comparison of the Fourier spectrum under El-Centro earthquake vibration between shaking table and smart phones with different types
2.5 测试精度检验:双向振动信号
采用图4所示固定方式,可获得智能手机在多向振动工况下的测试精度。图10,图11给出了1.6 Hz工况下,手机实测单轴加速度(分别给出x轴和y轴加速度时程)与振动台输出加速度在x,y轴方向上分量的时频域对比。

图10 1.6 Hz双向振动时程对比Fig.10 1.6 Hz two-way shaking table time domain result
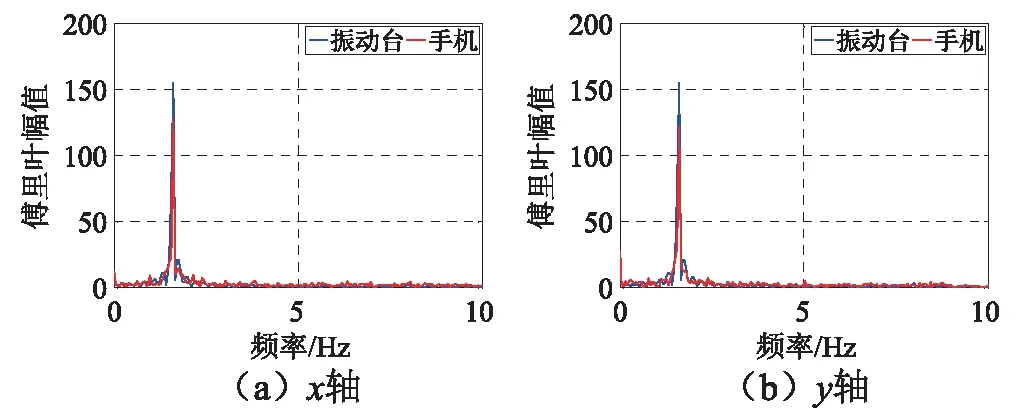
图11 1.6 Hz双向振动频域对比Fig.11 1.6 Hz two-way shaking table frequency domain result
结果表明,时域范围内,双向振动工况下的手机测试精度相对于单向振动工况下的测试精度明显降低:1.6 Hz工况下,手机x轴和y轴所记录到的峰值误差增加到27.5%和24.0%,显然测试时手机的放置方式对测试结果有影响。在频域内,手机测试信号主频与振动台输出信号主频基本一致,与单向振动工况下的测试精度无太大差别。
3 三维动作捕捉试验
上节一系列检验试验表明对于较低频率的周期性信号,固定良好的智能手机对指定方向具有很好的测量精度,因此可用于具有周期性的、低频行人运动的测试。本节利用三维动作捕捉试验进一步讨论手机行人荷载测试中的另外两个关键技术问题:携带方式和坐标转换。
3.1 三维动作捕捉技术
三维动作捕捉(3D Motion Capture Technology, 3DM)是利用多台红外摄像机捕捉测试对象上的反光标记物(称为Marker)空间运动轨迹的一种测量方法。
3.2 固定方式的影响
在行人运动状态下进行测试,手机可采用不同的固定(携带)方式。因此需要了解固定方式对测试数据可靠性的影响。试验中考虑了两种方式:一种是将手机放在裤子的口袋中并用手辅助固定,如图 12(a)所示;另一种采用腰带上加固定封套,将手机固定在测试者腰部靠近人体质心点的位置,如图 12(b)所示。以上两种固定情况下都有Marker点粘贴在手机上。测试者在外部节拍器的引导下,完成多种频率下的跳跃和屈伸。

图12 试验中的两种测试固定方式Fig.12 Two different installation methods in the test
对于跳跃和屈伸运动,图13是采用第一种固定方式的典型对比结果;图14是采用第二种固定方式的典型对比结果。可见,手机测试值的确受到固定方式的影响,第二种固定方式的测试精度优于第一种固定方式,测试结果更可靠。需要指出,第一种固定方式时手机实测信号的主频与试验中设定的频率一致,即此时部分测试结果(频率)可靠。这一数据低值的特点与庞大的手机用户数量相结合,对于未来构建居民可参与的大数据振动监测网络是有意义的。尽管结合下一小节讨论的坐标转换方法,可以适当放松对手机测试固定状态的要求,但实用中应尽可能采用稳定的固定方式以获得更理想的测试结果。这一结论显然与普通加速度传感器的使用要求是完全一致的。
3DM试验表明,稳定固定方式下,对于行走、跳跃和屈伸运动,手机的加速度测试精度与Marker点精度一致,可用于行人运动状态的测试。

(a) 2.0 Hz跳跃时手机信号与Marker点信号对比

(b) 2.0 Hz 屈伸时手机信号与Marker点信号对比图13 第一种固定方式下对比Fig.13 The comparison under the first fixed method
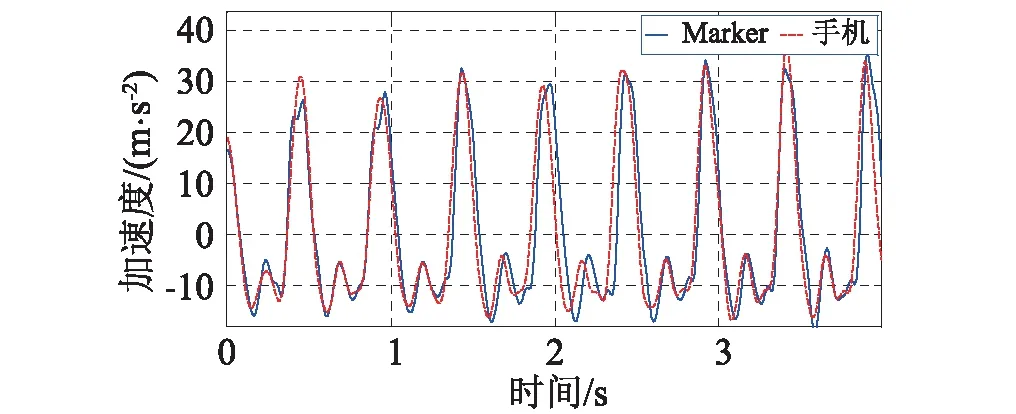
(a) 2.0 Hz跳跃时手机信号与Marker点信号对比

(b) 2.0 Hz 屈伸时手机信号与Marker点信号对比图14 第二种固定方式下对比Fig.14 The comparison under the second fixed method
表2,表3是各工况下手机数据与Marker的相对误差,表中不同字母代表不同的测试者,可见手机的加速度测试精度与三维动作捕捉技术的测试精度基本一致。
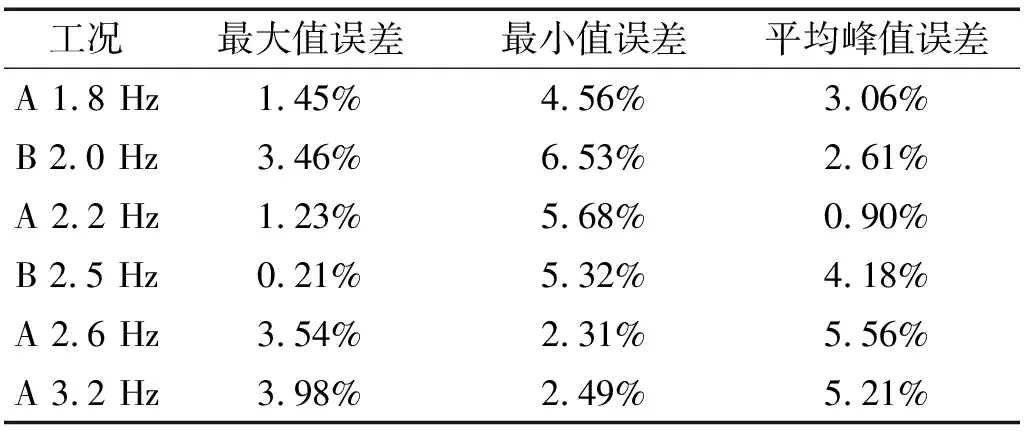
表2 屈伸运动各频率工况下的误差

表3 跳跃运动各频率工况下的误差
3.3 数据处理与坐标转换
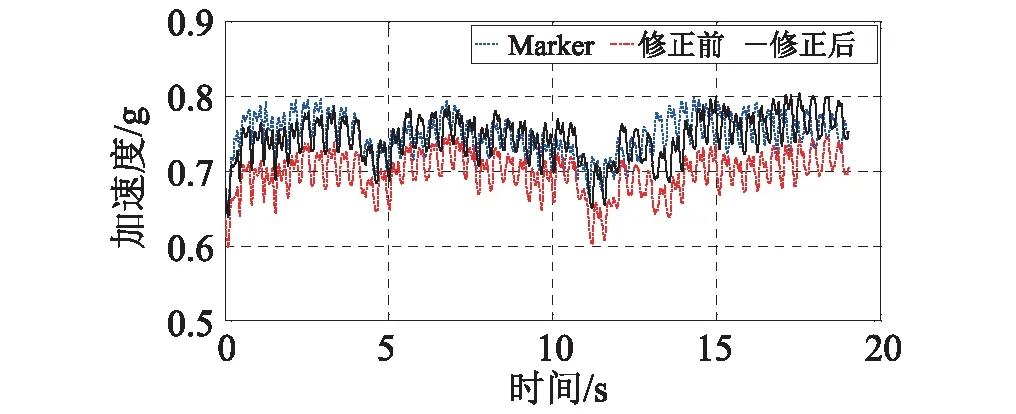
由于运动过程中手机的轴线指向可能存在偏转,需要将过程的测试值修正为初始设定的坐标轴方向。为此,首先在采用图1的垂直对中装置进行手机初始状态对中,即确定初始时刻手机的轴线方向,随后再固定在试验者腰带上进行测试。对手机记录结果进行9阶巴特沃斯低通滤波,截止频率为10 Hz,然后利用式(7)进行坐标转换。图15对比了2.6 Hz的屈伸工况时的修正前后的手机加速度信号的1sRMS和10sRMS值与Marker点对应结果,对比显示,经过坐标转换后的1sRMS值和10sRMS值与Marker点的对应指标更加接近,说明了坐标转换方法的合理性。
(a) 1s RMS值对比

(b) 10sRMS值对比图15 2.6 Hz 屈伸加速度值坐标修正前后 与Marker点加速度各指标对比Fig.15 The comparison of unrevised acceleration and revised acceleration between smart phone’s sensor and Marker under 2.6 Hz bounce case
4 基于智能手机的行人荷载实测
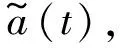
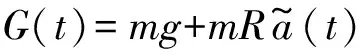
(9)
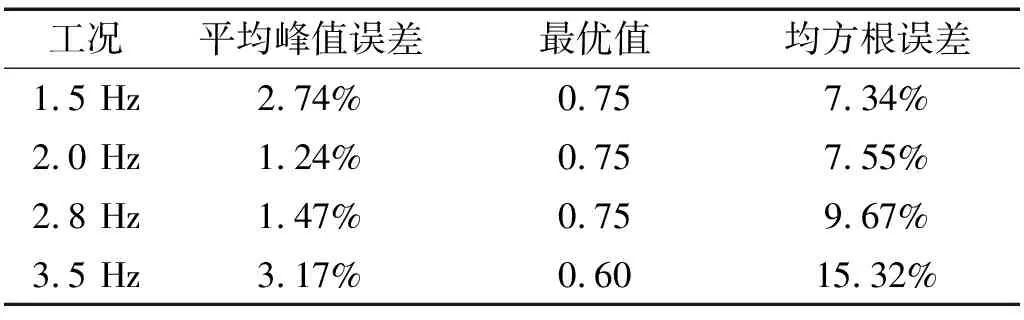
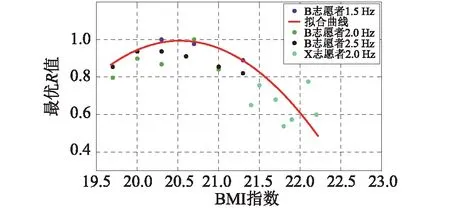
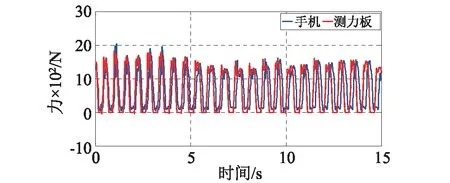
式中:G(t)为行人运动所引起的地反力,即行人荷载;m为行人的质量(kg);g为重力加速度(m/s2);R(0 通过对比测力板与式(9)的结果可以获得最优系数R:即式(9)计算行人荷载与测力板结果最接近时的R值。表4和表5所示为某位测试者在各不同工况下最优R值以及对应的计算荷载与实测荷载的均方根误差。 表4 不同屈伸运动工况下的误差及最优值 表5 不同跳跃运动工况下的误差及最优值 相关文献证明:身体质量指数(Body Mass Index,BMI)对人体运动姿态和足底压力起着至关重要的影响作用,因此可以建立振动参与系数与BMI的关系。四位测试者参加了实验,通过在在测试者腰部增加沙袋的方式来改变体重,共获得了十组不同BMI值下的R值(表6)。BMI指数计算方法如式(10)所示: BMI=M/h2 (10) 式中:M表示测试者总质量(kg);h表示测试者身高(m)。 表6为试验中不同测试者的BMI指数对应的最优R值和峰值误差。根据常见的人体BMI指数区间调查结果显示[9],将试验获得的R值和对应BMI指数在两个区间进行拟合,拟合公式为(11),结果见图16。 并给出屈伸运动的手机转化力和测力板实测结果对比情况(图17): (11) 表6 不同BMI值数下的误差及最优值 (a)范围1 (b)范围2图16 二次抛物线拟合最优值与BMI指数的关系曲线Fig.16 The relationship between the bestand BMI index by the method of parabolic fitting 式(9)同样适用于跳跃荷载,可采用相同的步骤获得R值与BMI的关系。本研究结果表明对于跳跃的R值受BMI影响不显著,大致在0.90~1.0之间,可统一取为0.95。对于步行荷载,作者此前的研究表明(张梦诗等,2013):单刚体模型获得的荷载模型计算值精度一般。而采用多刚体模型(如15体段的多刚体模型)可获得更高的精度,但模型对于测试数据量的要求也相应要提高。 利用手机获得行人的运动加速度后代入式(9)即可获得行人荷载。图17,图18给出屈伸、跳跃荷载与步行荷载的典型结果。计算时,屈伸的R值按式(11)计算,跳跃取0.95,步行取为0.55。计算结果与测力板结果的对比表明:对于屈伸荷载,手机测试结果的最大时域峰值误差在10%以内,精度较好,频谱的主峰值一致;对于跳跃荷载,手机测试结果的最大时域峰值误差在15%以内,调整R值后可获得更高精度的结果,频谱的主峰值一致;对于步行荷载,单个手机测试结果的精度一般,时域内波形和峰值都有偏差,但频谱的主峰值基本一致。 需要指出,本研究采用智能手机方法获得的人致荷载精度与采用Opal可穿戴式惯性传感器的最新跳跃荷载的研究文献[10]的现象一致:时域波形和主要峰值参数接近,频谱特性基本相同。上述结果以及其他领域的最新试验结果表明[11]:利用智能手机实现人体周期性动作的准确测试是完全可行的。 图17 Bounce工况手机测试值与测力板对比(1.5 Hz, R=0.728)Fig.17 The comparison of force got by smart phone and force got by force plate under bouncing load (1.5 Hz, R=0.728) (a)某志愿者跳跃工况手机转换力与测力板实测结果(1.5 Hz,数值法最优R=0.950) (b) 步行工况手机测试值与测力板测量值对比(右脚2.0 Hz,数值法最优R=0.550 3)图18 手机对人行荷载的测量与固定板测力结果对比Fig.8 The human load test results got by smartphones versus the results got by the force plate 本文通过一系列试验研究了智能手机进行行人荷载实测的可行性、实施技术和测试精度。 振动台试验结果表明,智能手机中所配置的加速度传感芯片的精度是测试精度主要影响因素[12-14]。采用集成最新硬件系统的智能手机型号配合具有高采样频率的数据采集软件,可准确获得谐波信号(1.5~3.4 Hz范围)的时频特征、扫频波的频谱特征,较为准确地得到扫频波的时域特征。对于地震波信号,智能手机系统的测量结果体现出有限价值:能反映信号的宏观时域特征,但在峰值大小、时刻以及频谱特性上,精度较差。 三维动作捕捉试验表明,智能手机系统可用于行人运动状态的测试,手机记录加速度值经过坐标转换后可准确反映行人步行、屈伸和跳跃运动时测量点处的加速度值。 测力板对比试验表明,手机加速实测值与人体运动的生物力学模型相结可获得行人荷载,荷载精度取决于力学模型的准确性。采用单刚体模型假定时,手机获得的屈伸和跳跃运动的荷载值精度较高,采用更准确的质量参与系数可进一步提升测试精度。对于步行运动,单刚体模型不适合,但手机测试结果的主频值有意义。4.1 振动参与系数R



4.2 行人荷载结果

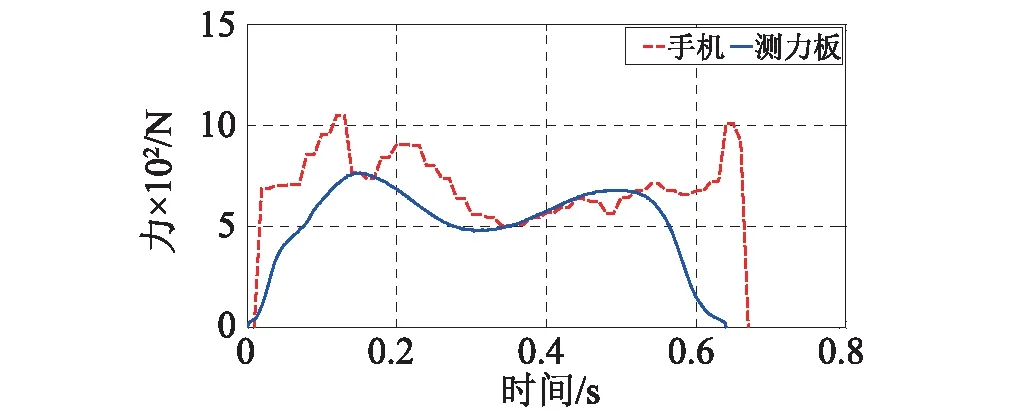
5 结 论
