中小跨径斜拉桥拉索监测方案研究
2022-02-25魏顺波
魏顺波
[林同棪国际工程咨询(中国)有限公司武汉分公司,湖北 武汉 430020]
0 引言
斜拉桥主要由索塔、主梁、斜拉索组成。斜拉桥是将主梁采用拉索锚固于桥塔上的一种结构形式,是由承压的塔、承弯的梁、受拉的索组合而成的结构体系。斜拉桥是用拉索取代桥墩支承的多跨弹性支承连续梁,其中拉索是斜拉桥的重要受力部件。为了保证桥梁的安全性,技术人员对拉索安全性评估作了较多研究。
由于中小跨径斜拉桥受到建设环境及经济条件的影响,一般未设置或只能在部分拉索上布置少量的传感设施来监测桥梁拉索的安全。如何将少量传感设施布置在桥梁拉索的恰当位置并取得最接近实际情况的数据就成为桥梁安全监测设计时需要处理的关键性问题之一,而恰当的位置只能通过拉索的相关性来确定[1],这也是本文研究的主要内容。
本文以武汉市光谷八路跨外环桥梁工程为背景,研究拉索之间的相关性,寻求最优拉索组合作为关联拉索,尽可能地反映桥梁的整体索力状态。
1 工程概况
武汉市光谷八路跨外环桥梁工程上部结构跨径布置为:2×30m(预应力混凝土连续箱梁)+(80+50)m(钢箱梁斜拉桥)+3×30m(预应力混凝土连续箱梁)+3×30m(预应力混凝土连续箱梁)。下部结构桥墩采用T形墩,桥塔采用“人”字形独塔,桥台采用桩柱式桥台。该桥主桥为典型的索辅梁结构体系。
基于Midas/Civil建立光谷八路桥主桥有限元模型(见图1),其中拉索编号奇数项为80m跨侧,偶数项为50m跨侧,由桥塔向两侧依次编号。对计算模型采用依次断开1根拉索,得到其他拉索的索力变化量,从而对计算所得的所有数据采用关联性分析,得到相关拉索的影响大小关系。

图1 光谷八路桥主桥有限元模型
2 数据分析
按照桥梁已有的设计参数,可以计算出本桥22根斜拉索在标准组合下的成桥索力,见表1。

表1 成桥状态下原始索力
将成桥时的状态作为第1施工阶段,然后依次钝化需要考虑断开的拉索作为第2施工阶段,以此为原则,依次设定断开拉索为各自的施工阶段,从而计算出在相同的原始索力下,依次断开每根拉索而导致的其他拉索索力变化。
由于计算数据较多,难以分析其规律性,现选取断开拉索T1和T12为例,分析其余拉索的索力变化特点。
断开拉索T1后,其余拉索的索力变化见图2;断开拉索T12后,其余拉索的索力变化见图3。
由图2、图3可知,在断开单根拉索时,其同侧拉索索力变化较大,另一侧拉索索力变化较小。因此本文将22根拉索分成2组,假定80m跨拉索为A,50m跨拉索为B,由桥塔向两侧依次重新编号,并进行相关性研究。考虑到每根拉索的原始索力不同,因此采用索力变化量/索力原始量,即索力变化率来优化处理计算数据。根据优化处理计算数据可以得知,断开某根拉索后,与其相近的索力变化率较大,随着距离增大,索力变化率基本呈现下降趋势(个别拉索如A10、B3、B4的索力变化率不符合此规律是因为其初始索力较相邻拉索索力差值过大,导致部分拉索断裂后,计算得到的索力变化率偏大)。
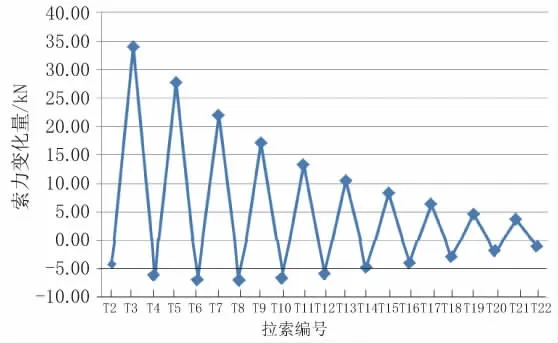
图2 断开拉索T1后其余拉索的索力变化

图3 断开拉索T12后其余拉索的索力变化
3 基于拉索关联影响矩阵的研究
因为得到的数据都相近,难以直接判断拉索与拉索的相关性大小。为方便研究,本文采取设定阀值的方式,假定仅考虑阀值以内的拉索与断开拉索关联,阀值之外的拉索无需与断开拉索相关联。通过多方面对比,确定以索力变化率范围的均值作为阀值来筛选相应拉索,研究其与断开拉索之间的关联性[1]。以断开拉索A3为例,其造成同侧其他10根拉索索力变化率的平均值为0.0516,则索力变化率大于这个阀值的拉索A1、A2、A4、A5、A6被认为是与拉索A3相关。
按照此方法,将存在相关性的记为1,认为不用考虑相关性的记为0,可得出22根拉索之间的关联矩阵。
因此,可选择拉索A1、A4、A7、A11这4根作为80m跨的关联拉索,B1、B5、B8、B11这4根作为50m跨的关联拉索,通过在这8根拉索上布置传感器来反映整体拉索的索力状况,保证经济性和实用性。
说明:(1)选择关联拉索已将个别拉索索力变化率规律不符合总体趋势的剔除;(2)部分3根拉索也可以反映整体的关联性,但考虑到这种方式下数据过少且分散,数值拟合时无法得到准确的线性关系,故不作考虑。
4 基于关联性的拉索状态评估
为验证4根关联拉索的最优性,将选择80m跨的A1、A3、A5、A7、A9共5根拉索作为关联拉索与之对比。以断开拉索A2为例,分析4根、5根这2种关联拉索组合下索力状态评估的准确性。由于计算数据有限,为减小误差,借助Matlab数值分析软件,采用最小二乘法拟合3次曲线方程。
4.1 5根关联拉索
模拟断开拉索A2,可得到测点拉索(5根)的索力变化率,见表2。

表2 断开拉索A2后测点拉索(5根)的索力变化率
拟合得到的曲线方程为:

如图4所示,y取最大值时,x=2.0628,故可判断是拉索A2断裂。
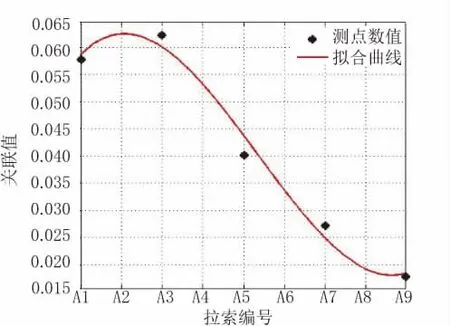
图4 断开拉索A2后测点拉索索力(5根)的关联值
4.2 4根关联拉索
模拟断开拉索A2,可得到测点拉索(4根)的索力变化率,见表3。

表3 断开拉索A2后测点拉索(4根)的索力变化率
拟合得到的曲线方程为:

如图5所示,y取最大值时,x=1.6142,故可判断是拉索A2断裂。

图5 断开拉索A2后测点拉索索力(4根)的关联值
综合2个结果可以看出,80m跨在2种关联拉索状态下,都可以评估拉索A2的索力状态。在考虑经济成本后,优先选择A1、A4、A7、A11这4根作为关联拉索,并模拟断开拉索A3进行验证。
模拟断开拉索A3,得到测点拉索索力变化率,拟合得到的曲线方程为:

如图6所示,y取最大值时,x=3.0964,可判断是拉索A3断裂。
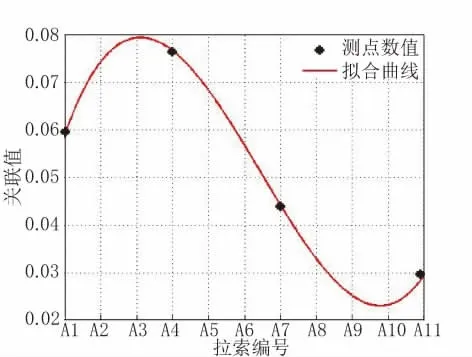
图6 断开拉索A3后测点拉索索力(4根)的关联值
5 结 语
(1)通过计算模型模拟拉索断开后,其余索力的变化情况来分析各根拉索之间的关联性大小,选出能反映全桥索力状态的最优拉索组合,布设传感器,再根据监测数据评估拉索状态,既可保证桥梁结构安全,同时也可节约监测成本。
(2)本文所选工程中部分拉索原始索力相比其他拉索差距较大,导致采用索力变化率的方式不能全面反映所有索力之间的相关性,可能与现实情况存在误差。
(3)根据索力的变化规律可以知道,并非所有拉索都能通过拟合3次曲线计算其最大值来作为评估手段的。
(4)本文在处理数据时采用的索力变化量与原始索力之比,可能会导致得出的相关性误差较大,后期将考虑灰色关联度和神经网络算法,来优化拉索之间的相关性。
(5)本文仅考虑了单根拉索断开时的关联性,并且只有理论计算数据,暂无实测数据进行验证。
(6)本文所选的实际工程为独塔单索面索辅体系,所得结论没有普遍性,对于双塔双索面和独塔双索面没有进行对比分析。
