衬砌脱空对隧道地震响应影响的振动台试验研究

丁祖德， 张 博， 李晓琴， 黄 娟， 彭立敏

(1. 昆明理工大学 建筑工程学院，昆明 650500； 2. 中南大学 土木工程学院，长沙 410075)

近30年，山岭隧道地震破坏较为频繁[1-3]。震害调查显示，在隧道洞口段、断层破碎带等地段易出现隧道震害，这些地段的隧道地震研究成果也较多。如蒋树屏等[4]基于公路隧道洞口段地震响应的振动台模型试验，得出惯性力对洞口段结构地震反应影响不大，抗震重点是围岩的失效防治。李林等[5]对浅埋偏压洞口段铁路隧道开展了振动台试验和动力分析，指出地表临空坡面会明显增大偏压隧道地表加速度放大倍率和位移值，衬砌拱顶两侧约45°位置和墙脚处为震害易发部位。崔光耀等[6-8]结合振动台模型试验分析了跨断层隧道动力特性及震害机理。耿萍等[9-10]完成了跨断层隧道抗减震措施效果的模型试验，结果表明设置减震层是提高隧道抗震性能的有效手段。但事实上，除了隧道洞口浅埋段及断层破碎地段外，隧道深埋洞身普通段衬砌也有不少严重破坏现象，甚至出现二次衬砌垮塌。如日本新泻地震中的Uonuma隧道，汶川地震中的酒家垭隧道、龙溪隧道、龙洞子隧道等[11-12]。日本Uonuma隧道衬砌垮塌后，调查发现衬砌背后存在较大空洞；龙溪隧道的震害调查发现，衬砌整体垮塌段存在衬砌背后不密实，在施工过程中曾经出现过围岩大变形；龙洞子隧道经现场地质雷达检测，震害部分区段衬砌拱顶处存在脱空和不密实情况。台湾集集地震中，大约75%的受损衬砌位于施工质量差的区域。可见，衬砌背后空洞及厚度不足等缺陷是造成震害的重要因素。

随着运营隧道的日益增多及既有服役隧道质量状况不甚理想的现状[13]，既有隧道抗震性能研究已引起国内外学者的逐渐重视。Hwang等[14]采用经验方法评估了老旧铁路隧道的抗震性能。Gome等[15]探讨了隧道开挖引起的应力扰动对已建地铁隧道地震响应的影响，结果表明应力扰动会明显增大衬砌的地震响应。邓涛等[16]运用有限差分软件，开展了不同加固方法处理龙门隧道衬砌背后空洞的抗震稳定性计算。于媛媛采用拟静力方法，聂子云等[17]采用动力有限元方法，分别研究了衬砌背后空洞对隧道结构抗震性能的影响。但总体而言，上述缺陷隧道的抗震研究多采用定性分析、简单数值模拟等，尚未有针对性的振动台模型试验。鉴于此，本文采用振动台模型试验研究隧道拱顶衬砌背后空洞及衬砌厚度不足对隧道地震响应的影响，分析不同空洞规模及衬砌厚度不足程度下隧道结构的地震响应规律，为高烈度地震区既有山岭隧道的地震安全评价及隧道加固设计提供依据。

1 振动台模型试验设计

1.1 模型试验内容

试验模拟对象为存在衬砌厚度不足与空洞缺陷的某Ⅳ级围岩段两车道高速公路隧道，隧道埋深30 m，净宽11.16 m、净高8.71 m，采用C30素混凝土衬砌结构，完好衬砌厚度40 cm。根据试验目的，共设置4组工况，具体见表1。其中，对于衬砌厚度不足的情况，采用对该部位衬砌减薄来实现(为方便表述，以下采用衬砌厚度减薄来描述厚度不足情况)。脱空范围以隧道拱顶圆弧圆心为基准展开，取约30°范围对于衬砌减薄25%，取约42°范围对于衬砌厚度减薄50%。试验时，制作一个薄拱形结构设置在围岩和衬砌之间来模拟衬砌背后空洞。

表1 试验工况

1.2 模型相似比设计

综合考虑振动台台面尺寸、隧道断面大小和边界效应，根据相似理论，以长度、质量密度和弹性模量为基本物理量，确定试验的几何相似比为Cl=1/40，密度相似比Cρ=1，弹性模量相似比CE=1/40，模型体系各物理量的相似关系及其相似比见表2。

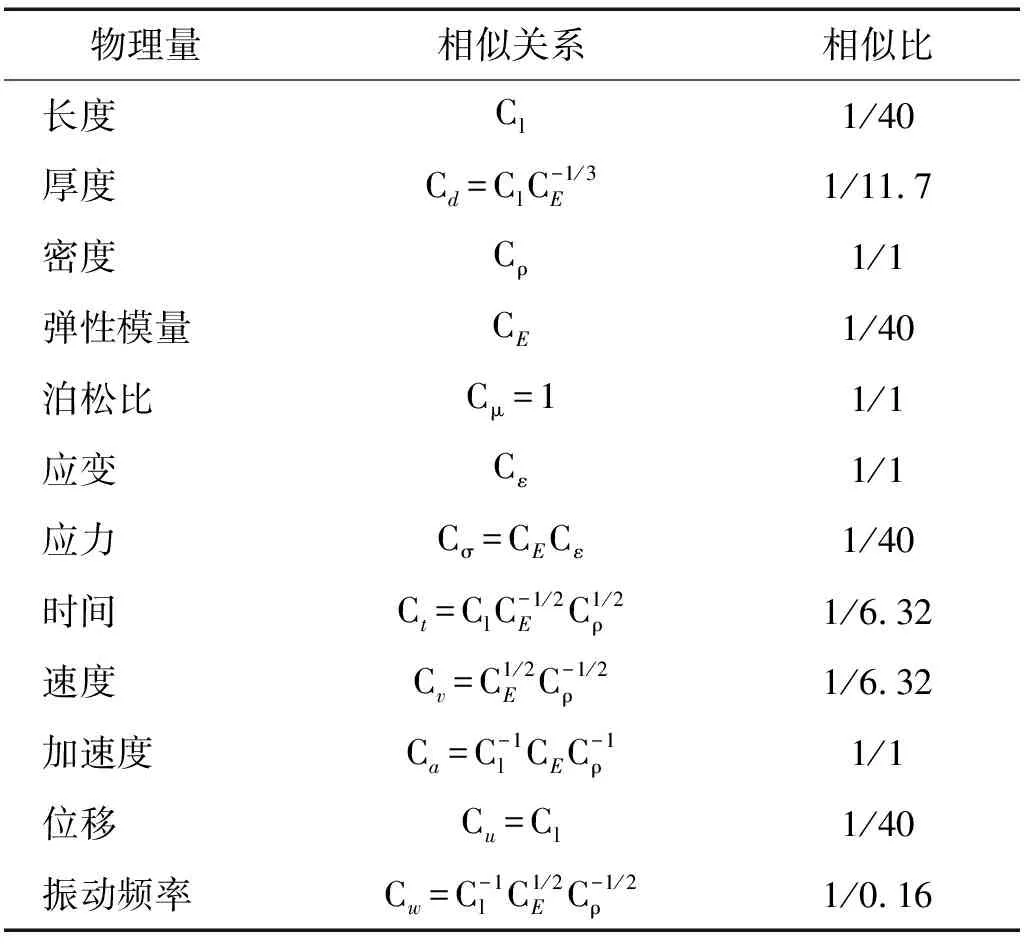
表2 模型相似比

1.3 试验材料及模型制作

选择合适的模型相似材料是模型试验中关键的一环，直接影响着试验结果的可靠性，根据现有试验研究成果，隧道衬砌相似材料主要采用微粒混凝土和石膏两种，围岩相似材料主要分为以沙、粉煤灰等为骨料，配以甘油、水等为黏结剂配比而成，或采用多种化学材料相互配比而成。经对材料配比试验的多方尝试和综合比较，选择微粒混凝土作为衬砌模型材料，由于衬砌模型厚度薄，将钢筋放入衬砌困难，故本文衬砌模型未考虑钢筋。选择砂、水泥、渣土及水混合作为围岩相似材料。经设计正交表格，进行单轴压缩试验，测试其强度、弹性模量和泊松比。经过多次配比试验后确定隧道衬砌结构质量配比为水泥∶细砂∶水=1.2∶4∶1，Ⅳ级围岩相似材料质量配比水泥∶粗砂∶土∶水=1∶15∶5∶2。加工完成后的减薄衬砌模型见图1。

图1 衬砌模型Fig.1 Lining model

1.4 模型箱设计

模型箱整体尺寸为2.0 m×2.2 m×1.6 m(横向×纵向×垂向)，底板平面尺寸3.0 m×2.5 m(横向×纵向)。模型箱主体框架由12#槽钢钢焊接而成，采用4 mm厚钢板做围护， 6 mm厚钢板做底板，正面中心设有预留观察孔，方便传感器线路连接。模型箱四周底部设有挂钩方便起吊，采用M20螺栓固定于振动台孔位上。箱体垂直和平行振动方向分别内衬厚度约20 cm和10 cm的聚苯乙烯泡沫层以减小边界效应。模型箱底部铺设黏结一层碎石，以增大与模型箱底板的摩擦阻力，避免试验激振过程中的滑移。模型箱加工效果见图2。

图2 试验模型照片Fig.2 Photo of experimental model

1.5 测试方案设计

四个衬砌模型沿纵向均匀布置，为方便安放，将工况1和工况2的衬砌模型置于两端，依次为工况2、工况4、工况3和工况1衬砌模型的布置方式。各衬砌模型纵向长度50 cm，模型之间相对独立，采用胶做简单粘结处理。地震波加载方向与隧道纵向垂直，选取每个模型的中间部位作为测试截面。采集数据包括围岩及衬砌结构的加速度、衬砌结构动应变、动态接触压力，分别布设加速度传感器、应变片及土压力盒。加速度传感器的布设见图3，各衬砌模型测试布置方案见图4(图中，A：加速度传感器，S：应变片，P：压力盒传感器)。

本次振动台模型试验共布置了8个加速度传感器、81个应变片和6个土压力盒，在离洞口分别为75 cm和140 cm处的衬砌内安装了2个高分辨率摄像头，实时记录振动时的裂纹发展。还在洞口架设了一台摄像机，用于捕捉洞口衬砌的破坏情况。

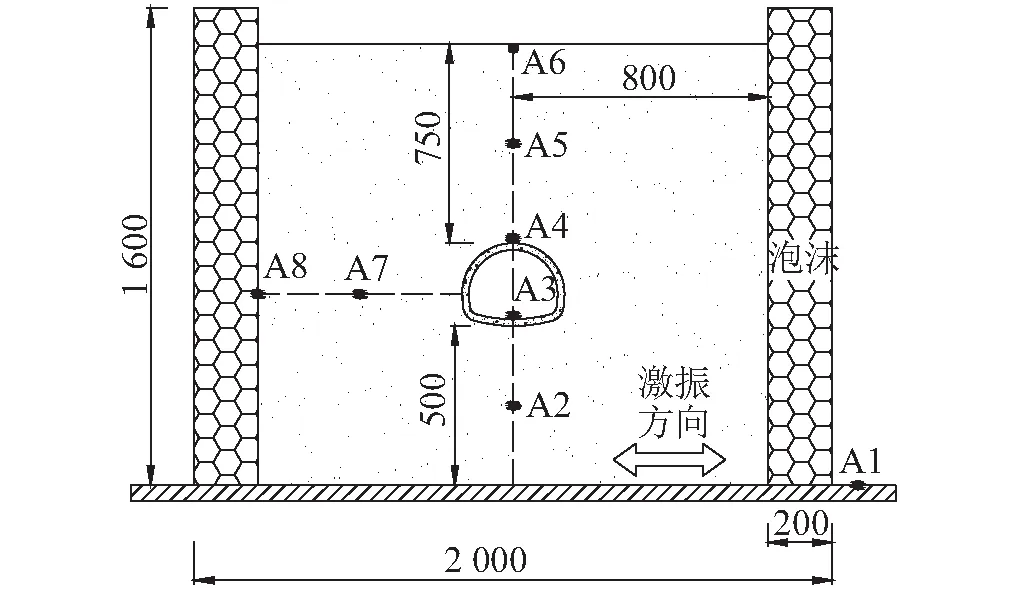
图3 加速度计布设示意(mm)Fig.3 Layout of accelerometers (mm)

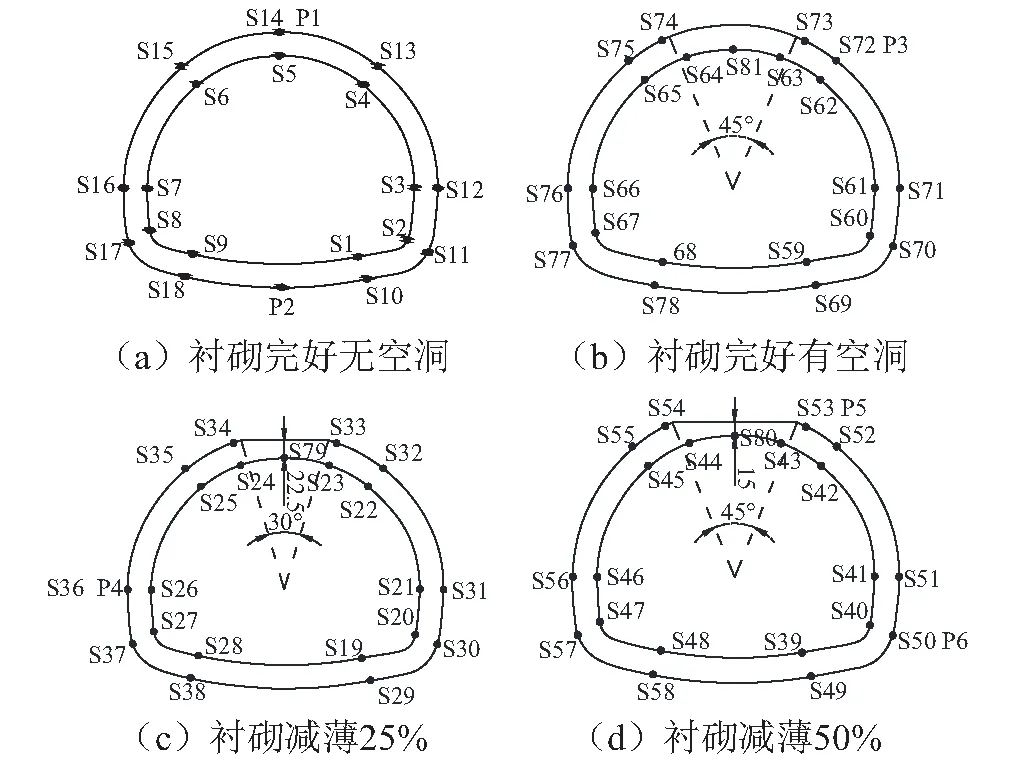
图4 衬砌模型测点布置Fig.4 Layout of monitoring points on lining model

1.6 地震动参数输入

试验采用按时间相似比压缩后的EI Centro波和Kobe波，单向激振，地震动持时约9 s，地震动峰值分别按0.1 g、0.2 g、0.3 g、0.4 g、0.6 g和1.0 g逐渐增加，以模拟不同地震强度。EI Centro波时间压缩后振动台输入的加速度时程曲线见图5。在加载前，进行0.05 g的白噪声扫频，以获得模型的整体振动特征。

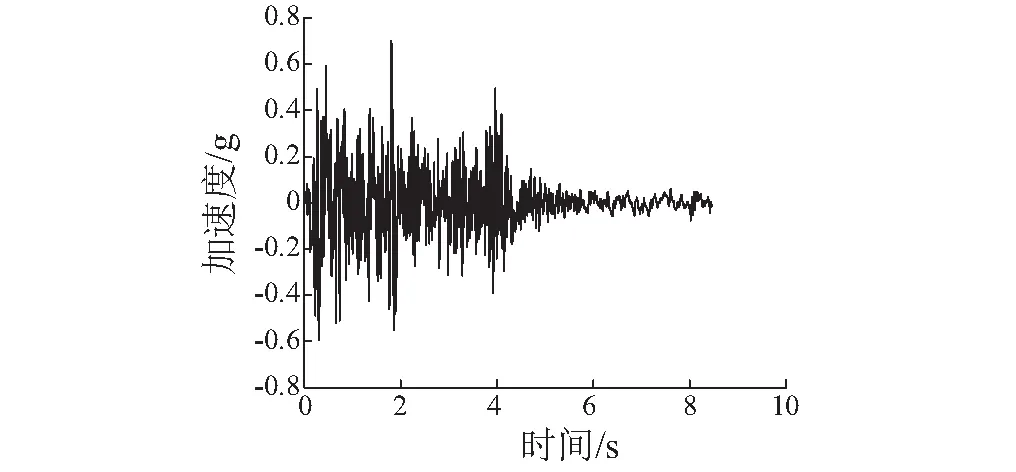
图5 EI Centro波加速度时程曲线Fig.5 EI Centro wave of dynamic calculation

2 试验结果及分析

本次试验测试了加速度、动土压力、动应变等参数，考察了EI Centro波和Kobe波两种地震波，限于篇幅，本文主要以EI Centro波为例进行分析。

2.1 加速度响应特征

模型试验中沿竖向和水平向埋设了8个加速度传感器，以测试隧道及围岩不同位置的加速度响应。图6为不同地震动强度下加速度放大系数随模型高程及横向距离的变化曲线。图中的加速度竖向放大系数是指围岩中线和模型箱上所设A1～A6加速度传感器各测点处所得的加速度峰值(PGA)与对应台面实测加速度峰值(A1)之比，加速度横向放大系数是指沿隧道仰拱高度处横向布置的加速度传感器A3、A7、A8，所测加速度峰值与A3处加速度峰值之比。

从图6可知，同一加载强度下，随着高程的增加，各测点加速度放大系数均有明显增大趋势。在0.5 m以下高程处，竖向放大系数变化较平缓，在0.75 m以上时，放大系数增加较快，达到围岩顶面时，增大趋势有所减缓。这说明隧道的存在对周边围岩的加速度响应有放大效应，距离隧道越远，影响越小，所以放大系数增幅先快后放缓。较低地震动强度时产生的竖向放大效应更明显。横向放大系数表现为先增大后减小。从隧道中线向模型边界，横向放大系数逐渐增大，在接近模型围岩边界时趋于平缓，甚至有所下降。横向放大效应在加载较强地震动时更明显。这说明地震波在围岩传播过程中具有滞后作用，从而引起衬砌变形。

图6 加速度放大系数的变化曲线Fig.6 Curves of accleration amplification factor

2.2 应变响应特征

衬砌模型内外侧贴有应变片，监测地震过程中的环向应变。以0.2 g的EI Centro波为例，四种试验工况的衬砌应变峰值数据见表3。应变峰值分布见图7。

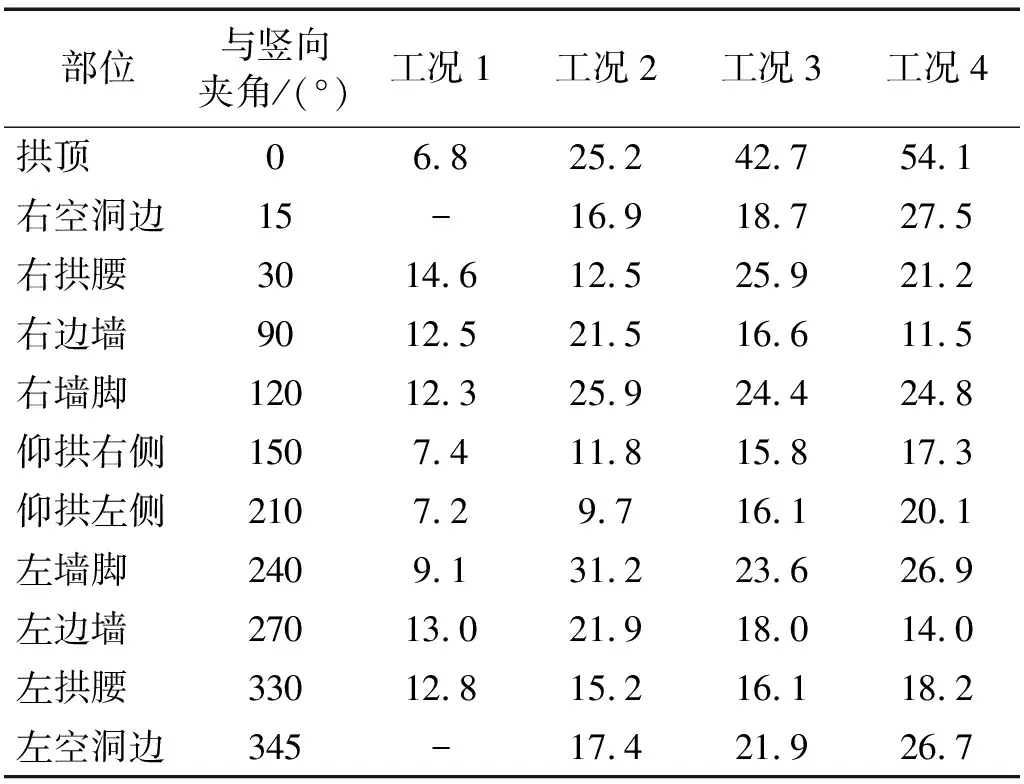
表3 衬砌各部位的环向应变峰值

图7 0.2 g EI Centro波下的衬砌应变峰值分布(με)Fig.7 Distribution of strains of lining under EI Centro wave input at 0.2 g (με)

表3和图7显示，当加速度峰值为0.2 g时，对于衬砌完好且背后无空洞的情况，其最大动应变峰值出现与隧道中轴线约呈45°的拱腰及墙脚部位，边墙部位也有较大的微应变，这与已有研究结论一致。对于拱顶衬砌背后存在空洞的情况，其拱顶应变增加明显，从工况1到工况4，应变增幅近7倍，这说明拱顶空洞的存在放大了该部位的震动效应。随着拱顶空洞及衬砌减薄程度的增加，拱顶及减薄边缘处应变不断增大，应变分布模式由花瓣状向竖向菱形状转变。可见，拱顶衬砌减薄及背后空洞，会改变衬砌结构的受力变形分布，缺陷部位变形增大，成为抗震薄弱部位。

2.3 衬砌破坏特征

在每次震动加载结束时，均进行隧道内表面裂缝等观察，并结合隧道内部的摄像头拍摄的地震过程响应情况，完整记录衬砌破坏过程。对于试验工况1，首次观察到可见裂缝对应的地震强度为0.6 g；对于试验工况2，首次观察到可见裂缝对应的地震强度为0.4 g；对于试验工况3和工况4，分别为0.3 g和0.2 g。图8和图9分别为试验结束时，试验工况1和工况2的衬砌开裂特征，图10为输入地震波0.3 g时拍摄的工况3的衬砌裂缝特征。

图8 试验工况1的衬砌开裂特征Fig.8 Cracks on model lining in test case 1

图9 试验工况2的衬砌开裂特征Fig.9 Cracks on model lining in test case 2

图10 0.3 g时的试验工况3衬砌开裂特征Fig.10 Cracks on model lining in test case 3 under EI Centro wave input at 0.3 g

从图8～10可看出，加载0.6 g的EI Centro地震波时，试验工况1的右墙脚靠近仰拱处、左侧墙脚及拱腰与边墙间均出现纵向贯通裂缝，最终破坏模式是与隧道中轴线约呈45°角的拱腰、墙脚部位开裂为特征。输入加速度为0.4 g时，工况2的拱顶、拱腰与边墙间及墙脚首先出现裂缝，之后仰拱出现裂缝。最终破坏部位位于拱顶、拱腰、墙脚和仰拱处。对于工况3和工况4，通过隧道内摄像头拍摄画面显示，在输入加速度分别为0.3 g、0.2 g时，拱顶首先出现裂缝，之后墙脚开裂，并在后续加载中不断扩宽并破坏。可见，衬砌拱腰、墙脚及仰拱是隧道抗震的薄弱环节，而当拱顶衬砌存在缺陷时，将改变其破坏形式，破坏首先发生在缺陷部位，并在较小地震动下就会引发裂缝。

3 结 论

(1) 地震动竖向放大系数随高程增加而增大，在0.5 m以下高程处增速相对平缓，隧道结构以上部分围岩放大系数增速显著提高，临近模型顶部时增幅又有所减缓。说明隧道的存在对周边围岩的加速度响应有放大效应。横向放大系数表现为先增大后减小，地震波在围岩传播过程中具有滞后作用，引起岩土体位移差，从而导致衬砌结构变形。

(2) 当隧道拱顶衬砌背后存在空洞缺陷时，拱顶应变值大大增加，增幅2.7倍，明显改变了拱顶处的受力状态，在地震强度为0.4 g时已出现可见裂缝。当同时存在衬砌厚度不足及背后空洞缺陷时，不仅改变了拱顶处的约束条件，而且衬砌的承载能力进一步弱化，在地震波作用下其受力状态及变形特征均有明显变化，拱顶处首先产生裂缝，应变增幅近7倍，在0.2 g的较小地震波强度下就已破坏。

(3) 缺陷的存在改变了衬砌地震破坏形式。对于完好衬砌，其破坏形态为与隧道中轴线约呈45°角的拱腰、墙脚部位开裂为特征；对于空洞缺陷，其最终破坏以拱顶、墙脚和仰拱部位裂缝为特征；对于衬砌厚度不足且有空洞缺陷，其破坏均以拱顶及墙脚开裂为主，只是破坏时峰值加速度不同，缺陷程度增大，破坏时的地震动强度越小。

(4) 本次振动台模型试验是基于横向地震波作用下衬砌脱空对结构地震响应的影响，不同地震波入射方向下缺陷衬砌结构的动力响应有待进一步深入研究。