江阴大桥船撞期间实测数据时间同步分析

王伟东， 姜绍飞， 周华飞， 韩 悦， 杨 蜜

(1.福州大学 土木工程学院，福州 350108； 2.温州大学 建筑工程学院，浙江 温州 325035)

江阴大桥为一座主跨1 385 m的悬索桥，是我国首座主跨超千米的桥梁。在施工期间，江阴大桥既已安装了结构健康监测系统[1-2]，是20世纪90年代末少数装备了结构健康监测系统的桥梁之一。2004年10月，江阴大桥结构健康监测系统启动了升级改造。在此期间，江阴大桥靠近靖江一侧的主梁遭受了一艘打桩船的撞击。此时，传感器系统已完成升级并投入使用，它们成功捕捉了船撞期间的桥梁响应。但是，数据传输网络尚未完成升级，各个数据采集仪的内部时钟尚未同步，这导致不同数据采集仪所采集的数据出现时间不同步。而且，该问题是因数据采集仪未经同步而引起的，实测数据之间的相对时间延迟量级可能非常之大。船撞期间的实测数据对于桥梁撞后评估的重要性不言而喻，然而，实测数据的时间不同步可能导致错误的分析结果。时间不同步的直接影响是数据之间的相位信息将发生偏差，而相位信息则是结构性能和损伤评估的重要指标[3-6]。因此，将江阴大桥船撞期间的异步数据同步化具有实际意义。

时间同步是无线传感器网络领域的研究热点。无线传感器网络中每个传感器节点都有自己的时钟，而所有时钟的时间可能并不同步。另外，不同传感器的采集启动时间不同、各个传感器节点的采样频率不同、以及传感器节点的采样频率随时间而变化等都会导致无线传感器网络的同步性问题。为解决这个问题，在无线传感器网络的软件与硬件方面都提出了一些解决方案，其中，研究最为广泛的是时间同步协议，如：RBS (Reference Broadcast Synchronization)[7-9]、TPSN (Time-sync Protocol for Sensor Networks)[10]、FTSP (Flood Time Synchronization Protocol)[11]等。虽然时间同步协议能帮助无线传感器网络实现较高精度的时间同步[12]，但是它们并不适用于纠正实测数据的时间不同步问题。在这方面，现有研究仍十分有限。Lei等[13]提出了两个时间同步算法，即ARX[14](Auto-Regressive with Exogenous Input)和ARMAV[15](Auto-Regressive Moving Average Vector)。前者用于输出信号和输入信号之间的时间同步，而后者用于两个输出信号之间的时间同步。为评估无线传感器网络的时间同步精度，Lynch等[16]采用无线信号与参考有线信号之间的最小误差范数，确定两者之间的时间延迟。类似地，Shen等[17]则采用无线和有线传感器数据之间的互相关函数，获得它们之间的时间延迟。然而，上述研究仅采用模拟数据进行验证，甚至未涉及任何验证工作。因此，江阴大桥实测异步数据的同步化值得深入研究。

本文采用状态空间(State space)模型对江阴大桥船撞实测数据进行时间同步分析。首先，任意选择其中一个加速度作为参考信号，而其余加速度作为时间平移信号，相对参考信号进行时间平移。然后，以一个参考信号和一个时间平移信号作为输出变量，针对每个平移时刻，分别建立相应的状态空间模型。利用已建立的状态空间模型，即可得到与每个平移时刻相对应的预测误差，预测误差达到最小值时所对应的状态空间模型即代表真实系统的最优模型，而此时所对应的平移时间即为参考信号与时间平移信号之间实际的时间延迟。本文首先以江阴大桥船撞期间的实测加速度数据展开时间同步研究，并借助船撞引起的桥梁加速度特征，采用直接对齐加速度峰值的方法与状态空间模型识别方法进行相互交叉验证。然后，利用船撞前的加速度数据，对状态空间模型方法识别时间延迟的可重复识别能力和精度进行分析与验证。最后，本文又利用船撞后时间同步的加速度数据对状态空间模型方法的抗伪识别能力进行了检验。

1 实测数据

升级改造后的江阴大桥结构健康监测系统包括位移、应变、加速度、温度、风等监测内容。本文仅对加速度数据进行分析，故这里仅介绍振动监测系统，如图1所示。江阴大桥主跨钢箱梁共布置了15个加速度传感器，分别布置在主跨的1/8、1/4、3/8、1/2和3/4断面处。每个断面上分别布置3个加速度传感器，其中一个安装在桥面的中心位置以测量横向加速度，另外两个则分别放置在桥面两侧以测量竖向加速度。图2为江阴大桥数据采集仪的布置图。江阴大桥共布置了8个数据采集仪，其中6个置于钢箱梁内，其余2个分别位于前、后锚室内。1/8、1/4和3/8断面上的加速度传感器分别与数据采集仪DAU3、DAU4和DAU5连接，而1/2和3/4断面处的加速度传感器则均连接到数据采集仪DAU7。加速度的采样频率为50 Hz，每小时数据保存为一个文件。

图1 江阴大桥主跨钢箱梁的加速度传感器布置图(m)Fig.1 Deployment of accelerometers on the deck of the Jiangyin bridge(m)

图2 江阴大桥的数据采集仪布置图(m)Fig.2 Deployment of DAUs on the Jiangyin bridge(m)

图3为江阴大桥船撞期间桥面横向加速度实测数据。船撞发生在2005年6月2日20点14分左右。由图可见，加速度AD9CL与AD13CL在该时段内有且仅有一个显著事件发生，因此，推断该事件由船撞引起。比较加速度AD9CL与AD13CL出现显著事件的时间可知，两者之间确实存在着显著的时间延迟，它们的加速度峰值之间的相对延迟时间为523.64 s。由于船撞当时各个数据采集系统的内部时钟尚未同步，从而造成了如此之大的相对时间迟延。此外，在加速度AD13CL出现显著事件的同一时间，加速度AD11CL也出现了相似的事件，这一定程度上说明了它们是时间同步的。这与实际情况相符，因为它们连接在同一个数据采集仪上。然而，需要指出的是，加速度AD11CL和AD13CL中船撞事件峰值的出现时间是不同的。以20:00:00为起始时间计算，它们的船撞事件峰值分别出现在第336.08 s和第334.32 s，即两者的峰值出现时间相差1.76 s。因此，利用加速度峰值的出现时间只能粗略估计两者的时间延迟。此外，加速度AD11CL出现了多个显著事件，而且船撞引起的加速度峰值并非最大值，加速度AD5CL和AD7CL也存在相似现象。因此，利用加速度峰值对齐方法识别它们之间的时间延迟往往并不可行。一般而言，实测加速度数据往往并不存在已知的显著事件，这使得基于事件的时间延迟识别方法更不可行。图4为船撞两个小时前记录的桥面横向加速度实测数据。在这一小时内，加速度AD9CL和AD13CL未出现显著事件，而其它加速度则出现了多个显著事件，这再次说明上述简单方法是不可行的。因此，本文提出使用状态空间模型方法识别加速度之间的时间延迟。另外，为检验状态空间模型方法的抗伪识别能力，本文还选取了船撞数小时后时间同步的实测加速度数据进行了研究。图5为船撞后桥面横向加速度实测数据。由图可见，仅仅通过观察加速度时程无法判断它们是否时间同步。

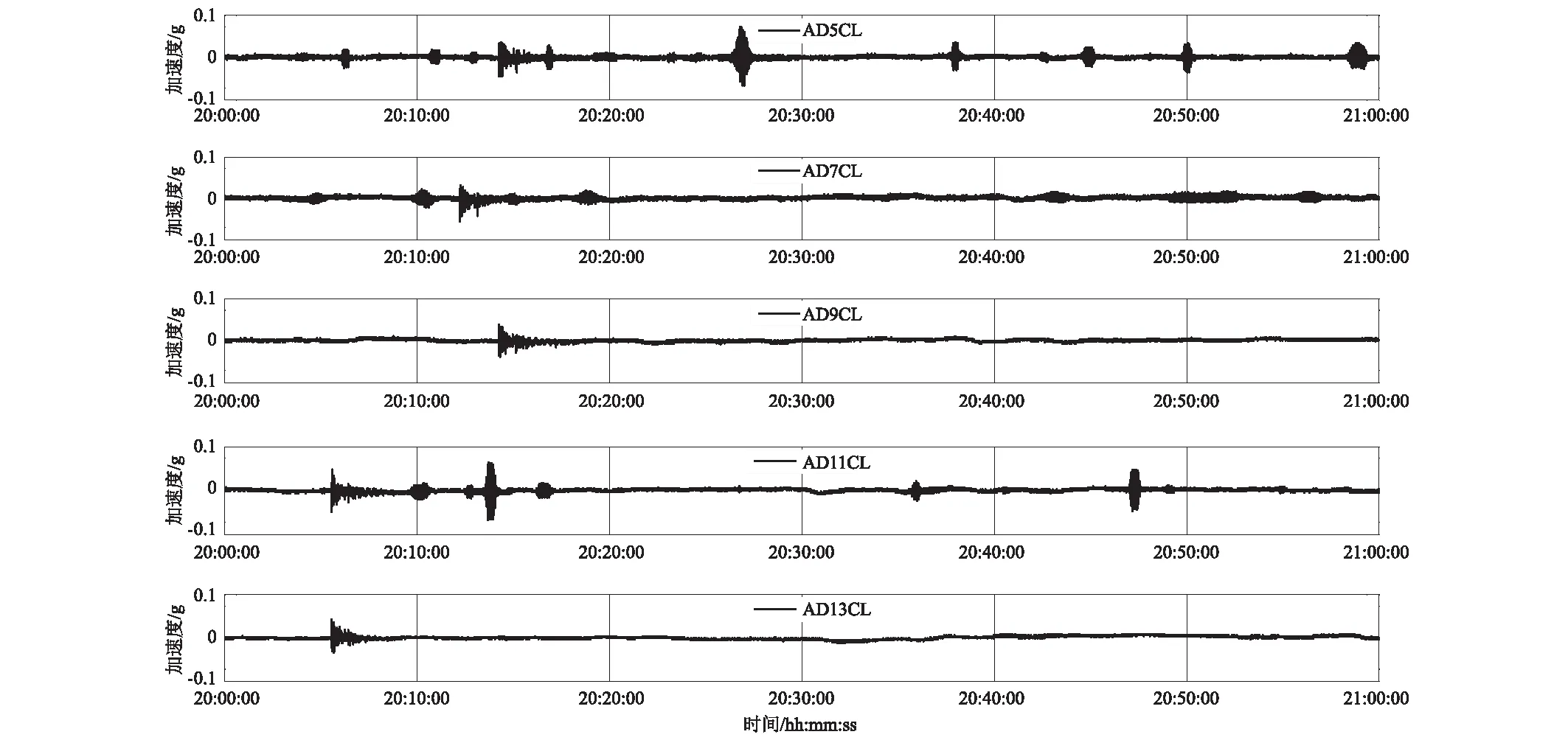
图3 船撞期间桥面横向加速度实测数据Fig.3 Lateral accelerations of bridge deck measured during ship-bridge collision

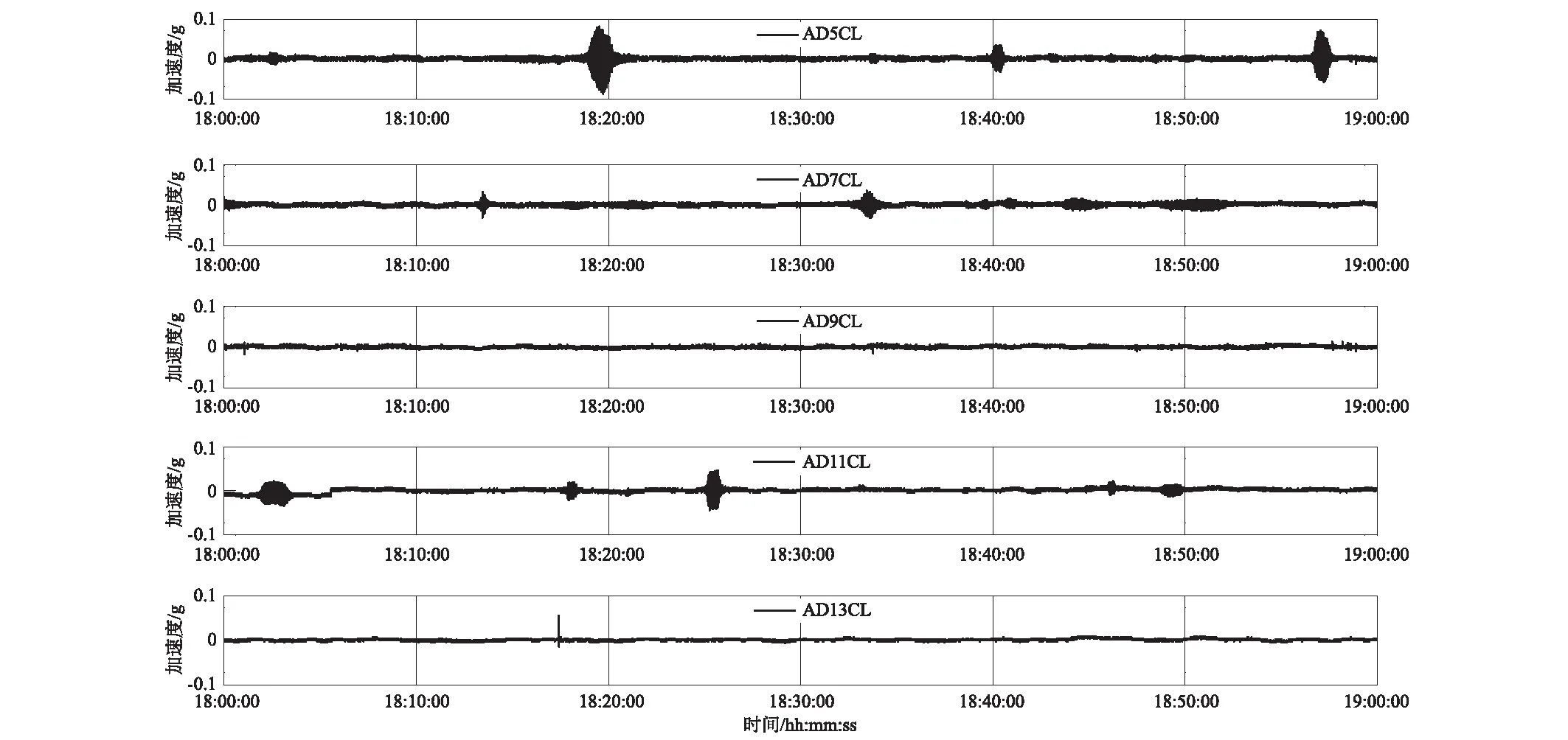
图4 船撞前桥面横向加速度实测数据Fig.4 Lateral accelerations of bridge deck measured before ship-bridge collision

图5 船撞后桥面横向加速度实测数据Fig.5 Lateral accelerations of bridge deck measured after ship-bridge collision

2 时间同步算法

2.1 状态空间模型

状态空间模型采用系统的输入、输出及状态变量之间的一阶微分或差分方程来描述一个系统[18-19]。它不仅能反映系统内部状态，而且能揭示系统内部状态与外部输入和输出变量的联系。状态空间模型由状态方程与输出方程组成[20-23]，即：

(1)

xk+1=Axk+wk
yk=Cxk+vk

(2)

式中：wk与vk为平稳的零均值高斯白噪声。

本文采用式(2)构建江阴大桥状态空间模型。给定模型阶数，式(2)中的系统矩阵A与输出矩阵C可由随机子空间识别(Stochastic Subspace Identification, SSI)方法估计得到。SSI方法可分为基于协方差的SSI方法与基于数据驱动的SSI方法[24-25]。基于数据驱动的SSI方法无需计算协方差矩阵，大大减少了运算时间和数据误差。因此，基于数据驱动的SSI方法比基于协方差的SSI方法更精确[26-27]。基于数据驱动的SSI方法的核心是将输出数据直接组成Hankel矩阵，将Hankel矩阵中的“将来”输出的行空间投影到“过去”输出的行空间，投影的结果保留了“过去”的全部信息，并用此预测“未来”信息。包含“过去”输出与“将来”输出的Hankel矩阵Y0, 2i-1可写为：

(3)

式中：Yp为mi×j“过去”输出矩阵；Yf为mi×j“将来”输出矩阵。然后，将“将来”输出的行空间向“过去”输出的行空间进行正交投影，投影矩阵Πi可表示为：

(4)

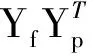
(5)

式中：Λi表示输出向量间时间间隔为i的输出协方差矩阵，定义为：

(6)

利用式(2)，Λi可写成：

Λi=CAi-1G

(7)

式中：G为状态向量xk+1与输出向量yk之间的状态输出协方差矩阵。将式(7)代入式(5)可得：

(8)

(9)

将式(8)、(9)代入式(4)，投影矩阵Πi可改写为：

(10)

C=Oi(1∶m, ∶)

(11)

而系统矩阵A也可从可观测矩阵Oi得到，即：

(12)

(13)

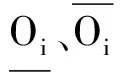
因此，若已知可观测矩阵Oi，即可求得系统矩阵A与输出矩阵C。为此，需要得到投影矩阵Πi。投影矩阵Πi可通过对式(3)进行QR分解得到：

(14)

式中：Q为正交矩阵；R为下三角矩阵。投影矩阵Πi经过适当变换[24]，写为

(15)

对式(15)得到的投影矩阵Πi进行奇异值分解可得：

(16)

式中：U与V为正交矩阵，UTU=UUT=I，VTV=VVT=I；S1为S从大到小排列由奇异值构成的对角矩阵；为矩阵中的非零奇异值。联立式(15)与式(16)可得：

(17)

(18)

综上所述，通过上式计算求得可观测矩阵Oi后，即可获得系统矩阵A与输出矩阵C。

2.2 时间同步分析

基于状态空间模型的时间同步分析方法的基本原理为：状态空间模型是代表实际系统的一个数学模型，若用于模型拟合的实测数据存在时间不同步，则由此建立的状态空间模型可能偏离真实系统，这将导致该模型的预测误差增大。因此，可以人为移动时间平移信号的时间轴，并针对每个平移时刻分别建立相应的状态空间模型。利用已建立的状态空间模型，即可得到与每个平移时刻相对应的预测误差，预测误差达到最小值时所对应的状态空间模型即是代表实际系统的数学模型，而此时的平移时间即为参考信号与时间平移信号之间的实际时间延迟。具体步骤为：首先，任意选取其中一个加速度作为参考信号，其时间轴固定不变。其余加速度作为平移信号，它们的时间轴以一定的时间间隔进行平移。需要指出的是，本方法的本质是寻求代表实际系统的数学模型，而数学模型的建立理论上应该不受参考信号选取的影响。然而，状态空间模型是一种基于数据驱动的方法，实际上数据质量的好坏将影响识别结果的精度，因此，参考信号的选取可能对时间延迟的识别结果产生一定的影响。但总体而言，参考信号的选取应不会显著影响时间延迟的识别结果。然后，针对每个平移时刻，以参考信号与平移信号组成输出向量，构建相应的状态空间模型，使用基于数据驱动的SSI方法估算系统矩阵。接着，将用于模型拟合的输出向量序列重新输入已建模型，获得输出向量的预测值，从而得到预测误差向量序列(即预测的和实测的输出向量序列之间的差值)。最后，计算预测误差向量序列的损失函数，将预测误差向量序列转化成一个可以比较的大小的实数。重复上述步骤，即可得到与平移时刻相对应的损失函数，而损失函数达到最小值时所对应的平移时间即为参考信号与平移信号之间的实际时间延迟。

本文采用AIC (Akaike’s Information theoretic Criterion)与FPE (Final Prediction Error)来估计模型阶次。AIC与FPE基于最大似然法估计模型阶次，是估计模型阶次最为常用的方法[28-30]。它们首先由Akaike提出，用于估计线性模型的泛化误差[31]。它们定义为：

(19)

式中：d为模型参数的总个数；N为模型拟合样本的总个数；ln为自然对数；V为损失函数，定义为：

(20)

式中：det为行列式；e为预测误差向量，即：

(21)

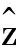
图6 状态空间模型识别延迟时间流程图Fig.6 Flow chart of state space model for the time lag

图6为时间同步分析流程图。在此，以江阴大桥船撞过程中的实测加速度为例，详细阐述状态空间模型用于识别时间延迟的过程。鉴于加速度AD9CL在船撞期间有且仅有一个显著事件，因此选取加速度AD9CL为参考信号。另外，由图3可见，其它加速度相对加速度AD9CL的时间延迟并不相同甚至相差甚远，若以所有加速度组成状态空间模型的输出向量，各个加速度间的平移时间的组合数量将是极其巨大的。因此，本文以一个参考信号(AD9CL)和一个时间平移信号(即AD5CL、AD7CL、AD11CL和AD13CL之一)为输出向量构建状态空间模型。特别地，加速度AD11CL与AD13CL连接在同一个数据采集器上，它们是时间同步的，但是，本文仍将参考信号(AD9CL)分别与平移信号AD11CL、AD13CL组成输出向量，构建状态空间模型，以检验状态空间模型的抗伪识别能力。为获得加速度间的实际时间延迟，往往需要考虑大量的平移时间，而这将需要大量的计算工作量。为平衡计算工作量与时间延迟精度，本文首先以5 s为时间步长获取时间延迟可能出现的区间，然后，在此区间内以1 s、0.1 s和0.02 s为时间步长进行更精细地搜索。值得注意的是，加速度传感器的采样频率为50 Hz，0.02 s是时间平移的最小时间步长。由于每个平移时间所对应的模型的阶数已采用AIC和FPE达到最优，由此得到的损失函数对于相应的平移时刻而言也是最优的。因此，可认为最小损失函数所对应的平移时间就是参考信号与平移信号之间的实际延迟时间。同样地，采用类似方法对船撞两个小时前的异步加速度实测数据和船撞后的同步加速度实测数据进行分析。船撞前的异步实测数据用于评估状态空间模型方法的可重复识别能力，船撞后的同步实测数据则用于检验其抗伪识别能力。

3 结果与讨论

3.1 船撞时段时间同步分析

以识别加速度AD9CL与AD7CL之间的时间延迟为例，详细说明异步数据的时间同步过程。根据图3，加速度AD7CL在20∶12左右出现的事件与AD9CL中船撞引起的事件具有相似的波形。因此，推断该事件同为船撞所引起，据此可估算它们之间的延迟时间的搜索范围。另外，为了测试状态空间模型抵抗其它事件干扰的能力，本文将延迟时间的搜索范围进一步加大，将船撞事件之前出现的另一个显著事件也包含其中。最终，加速度AD9CL与AD7CL的延迟时间的搜索范围确定为-280～0/s。对于每个平移时间，由AIC与FPE确定状态空间模型的最优阶数，由式(20)计算相应模型的损失函数。作为示例，图7给出了平移时间为-131.0 s时，AIC与FPE随模型阶数的变化图。显然，模型阶数为18时，AIC与FPE都达到最小值，则对应于此平移时间的状态空间模型的阶数确定为18。利用式(20)，可得该状态空间模型的损失函数值为8.77×10-11。图8为损失函数值随平移时间的变化图。为了平衡计算工作量与延迟时间精度，首先以5 s为时间步长确定时间延迟可能出现的范围，如图8(a)所示。可见，在-120 s之前，损失函数值随平移时间的增加而减小；此后，随着平移时间的进一步增加，损失函数则呈现明显的上升趋势。因此，可以推断加速度AD9CL与AD7CL之间的实际时间延迟在-120 s附近。另外，值得指出的是，延迟时间在-240～-180/s时，损失函数相对较大，而该时间段正对应于加速度AD7CL中船撞事件前发生的显著事件的出现时间，这一定程度上验证了状态空间模型抵抗其它事件干扰的能力。为了更精确地确定时间延迟，在-140～-100/s区间内以1 s、0.1 s和0.02 s为时间步长进行更精细地搜索，如图8(b)所示。可见，平移时间为-121.80 s时，损失函数到达最小值，故加速度AD9CL与AD7CL之间的实际时间延迟确定为-121.80 s。

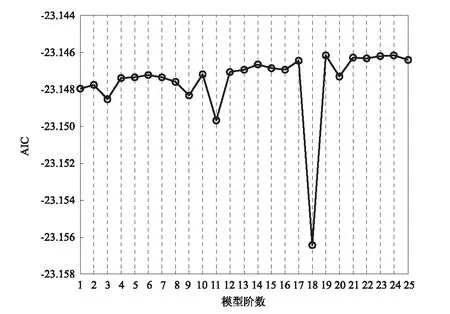
(a)AIC

(b)FPE图7 AIC与FPE随模型阶数的变化图Fig.7 AIC and FPE Versus Order of State Vector

同样地，加速度AD5CL、AD11CL、AD13CL与AD9CL之间的时间延迟也可以采用相同方法得到。表1列出了船撞时段实测加速度间的时间延迟。除了加速度AD5CL与AD9CL的时间延迟仅为0.44 s外，加速度AD7CL、AD11CL、AD13CL与AD9CL之间的时间延迟均较大，尤其是AD9CL与AD11CL、AD13CL之间的时间延迟达到了523.20 s，这是由于当时江阴大桥结构健康监测系统尚处于升级之中，各个数据采集仪的内部时钟尚未同步所致，这也说明了对江阴大桥船撞实测数据进行时间同步的必要性。对于加速度AD9CL与AD13CL，由状态空间模型得到的延迟时间为-523.20 s，而通过直接对齐加速度峰值时间估算得到的时间延迟则为-523.64 s，两者比较接近，这一定程度上验证了状态空间模型方法的正确性。此外，加速度AD11CL与AD13CL由状态空间模型识别得到的时间延迟均为-532.20 s，由于它们连接在同一个数据采集仪，它们之间应该是时间同步的，这从另一个角度验证了状态空间模型方法的准确性。利用识别得到的时间延迟，图9描绘了江阴大桥船撞期间时间同步后的实测加速度。由图可见，各个加速度在船撞期间均出现了相似的波形，这进一步验证了由状态空间模型方法识别得到时间延迟的准确性。以20∶00∶00为起始时间，表2列出了时间同步后船撞事件的峰值加速度的出现时间。可见，各个加速度出现船撞事件峰值的时间不尽相同。以加速度AD9CL为基准，峰值出现时间最大相差3.96 s(与加速度AD5CL)而最小相差0.44 s(与加速度AD13CL)。

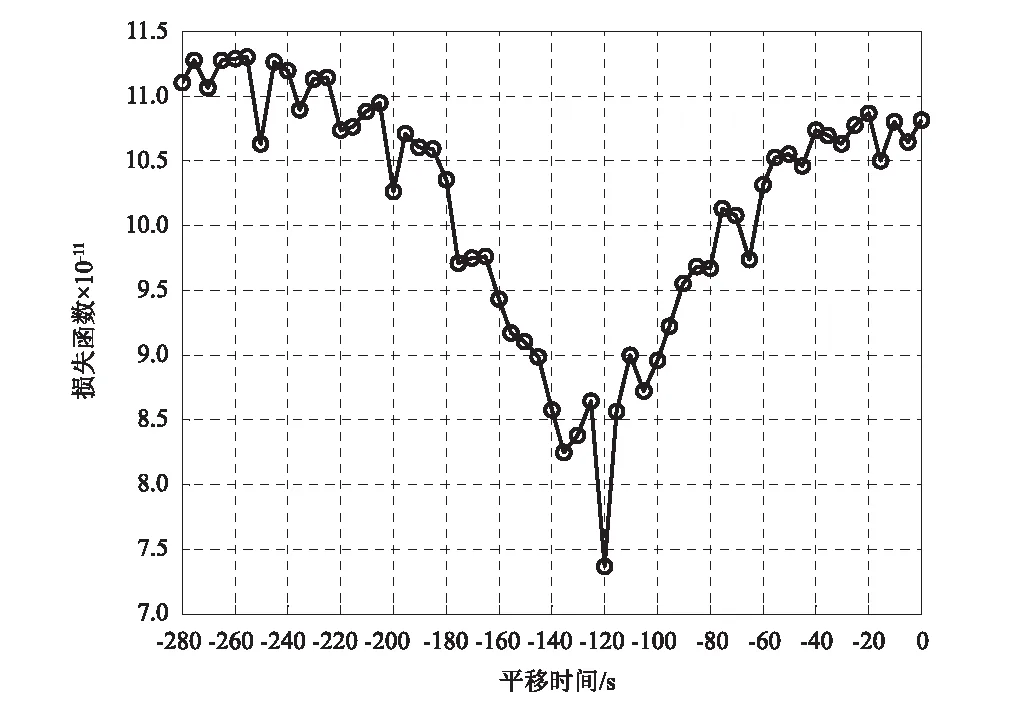
(a)-280 ～ 0/s

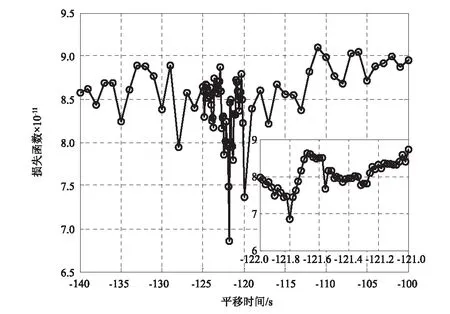
(b)-140 ～ -100/s图8 损失函数随平移时间的变化图(船撞期间的加速度AD9CL与AD7CL)Fig.8 Loss function versus shifting times for accelerations AD7CL measured during ship-bridge collision

表1 船撞期间实测加速度间的时间延迟

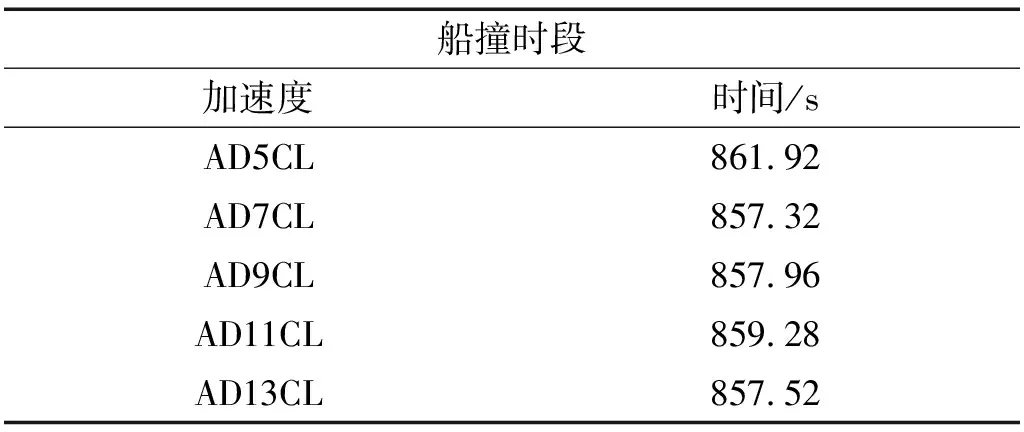
表2 时间同步后船撞事件的峰值加速度的出现时间

图9 时间同步后的船撞期间桥面加速度Fig.9 Time synchronized accelerations of bridge deck measured during ship-bridge collision

3.2 船撞前加速度数据同步分析

为了验证状态空间模型方法的可重复识别能力及精度，本文对船撞前两个小时记录的实测加速度数据也进行了同步分析。此时的实测加速度间的时间延迟应与船撞期间的实测加速度间的时间延迟相同。这里，仍以加速度AD9CL与AD7CL为例进行分析。此时，加速度AD9CL与AD7CL并无已知的显著事件可用于确定它们之间的时间延迟的搜索范围。鉴于船撞期间它们之间的时间延迟为-121.80 s，故将时间延迟的搜索范围定为-200～0/s。图10为损失函数随平移时间的变化图。如图10(a)所示，以5 s为时间步长所确定的损失函数的最小值不再出现在-120.0 s，而是出现在-115.0 s。但是，-120 s所对应的损失函数已经非常接近损失函数的最小值，因此，真实的时间延迟仍可能出现在-120.0 s左右。为更精确地获得实际的时间延迟，在-125～-105/s范围内以1 s、0.1 s和0.02 s为时间步长进行更精细地搜索，如图10(b)所示。由图可见，当平移时间为-121.94 s时，损失函数到达最小值，故加速度AD9CL与AD7CL间的时间延迟确定为-121.94 s。船撞期间它们之间的时间延迟为-121.80 s，这验证了状态空间模型方法识别时间延迟的可重复性及精度。不仅如此，加速度AD9CL在该时段并没有显著事件发生，状态空间模型能够在没有显著事件的帮助下而成功识别时间延迟，这进一步验证了状态空间模型方法的有效性。

(a)-200 ～ 0/s

(b)-125 ～ -105/s图10 损失函数随平移时间的变化图(船撞前的加速度AD9CL与AD7CL)Fig .10 Loss function versus shifting times for acceleration AD7CL measured before ship-bridge collision

表3列出了船撞前实测加速度之间的时间延迟。比较表1与表3可知，船撞前和船撞期间识别得到的时间延迟基本一致，这不仅交叉验证了所识别得到的时间延迟的正确性，而且也验证了状态空间模型方法识别时间延迟的可重复性。另外，值得重申的是，该时段内加速度并无已知的显著事件可供利用，而这恰恰也是实际应用中最常见的情况，状态空间模型能够在这种情况下正确识别时间延迟，这再次证实了状态空间模型方法的有效性。至于状态空间模型方法的精度，船撞前和船撞期间识别得到的延迟时间的最大偏差为0.28 s，出现在加速度AD9CL与AD5CL之间。作为一种基于数据驱动的方法，数据质量的好坏将影响识别结果的精度，本文所使用的数据来自一个实际大型结构在环境激励下的响应，实测加速度数据中不可避免存在噪声。而且，这些数据更是在结构健康监测系统还未进入正式运营的情况下获得的，这使得实测数据存在更多的不确定性，从而影响状态空间模型方法识别时间延迟的精度。因此，船撞前和船撞期间识别得到的延迟时间存在一定偏差是可以接受的。由表3可知，加速度AD11CL和AD13CL与AD9CL之间的时间延迟是相同的，这再次验证状态空间模型方法的抗伪识别能力。

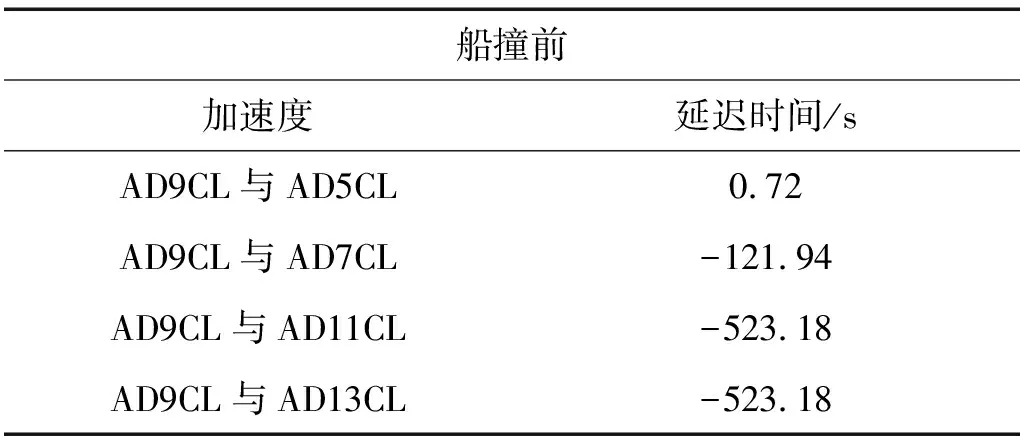
表3 船撞前实测加速度间的时间延迟

3.3 船撞后加速度数据同步分析

为了进一步测试状态空间模型方法的抗伪识别能力与精度，本文对船撞后时间同步的加速度数据也进行了分析。根据图5，该时段的加速度数据并无已知的显著事件可用于选择参考加速度，出于一致性考虑，这里再次将加速度AD9CL选作参考信号。由于此时数据是时间同步的，因此，将时间延迟的搜索范围定为-10～10/s。再次以识别加速度AD9CL与AD7CL的时间延迟为例，图11为损失函数随平移时间的变化图。由图可见，平移时间偏离0 s越多，则损失函数总体上越大。损失函数的最小值出现在0.00 s，故认为加速度AD9CL与AD7CL之间的时间延迟为0.00 s，这完全符合预期，因为它们是时间同步的。表5列出了船撞后实测加速度间的时间延迟。可见，加速度AD5CL、AD7CL、AD11CL和AD13CL相对加速度AD9CL的时间延迟都接近于0 s。其中，与实际延迟时间偏差最大的是加速度AD11CL和AD13CL，它们与AD9CL之间的时间延迟为0.20 s，这证实了状态空间模型方法的抗伪识别能力及精度。再次地，加速度AD9CL与AD11CL、AD13CL所识别得到的时间延迟是相同的。作为验证，以加速度AD11CL为参考信号，建立了其与加速度AD13CL之间的状态空间模型进行时间同步分析。图12为损失函数随平移时间的变化图。可见，虽然损失函数中出现了较多的局部波动，但是平移时间为0.00 s所对应的损失函数相对其它平移时间所对应的损失函数显著减小，因此，加速度AD11CL与AD13CL之间的时间延迟识别结果为0.00 s，这与实际情况相符，从而一定程度上说明本方法具有一定的抵抗局部干扰的能力。还需指出的是，状态空间模型是一种基于数据驱动的方法，数据质量的好坏将影响识别结果的精度，损失函数的局部波动可能引起时间延迟识别结果出现误差。但是，随着平移时间远离实际延迟时间越多，损失函数总体上呈现明显的上升趋势，这点已在图8(a)和图10(a)中得到充分说明。因此，即使因损失函数局部波动而引起时间延迟识别结果出现误差，由此引起的误差也应是可控的。另外，值得提及的是，以加速度AD9CL为参考信号，分别建立其与加速度AD11CL和AD13CL之间的状态空间模型时，结果同样表明加速度AD11CL和AD13CL是时间同步的。因此，无论选取加速度AD9CL或AD11CL作为参考信号，结果均表明加速度AD11CL和AD13CL是时间同步的，这一定程度上验证了参考信号的选取应不会显著影响时间延迟的识别结果。

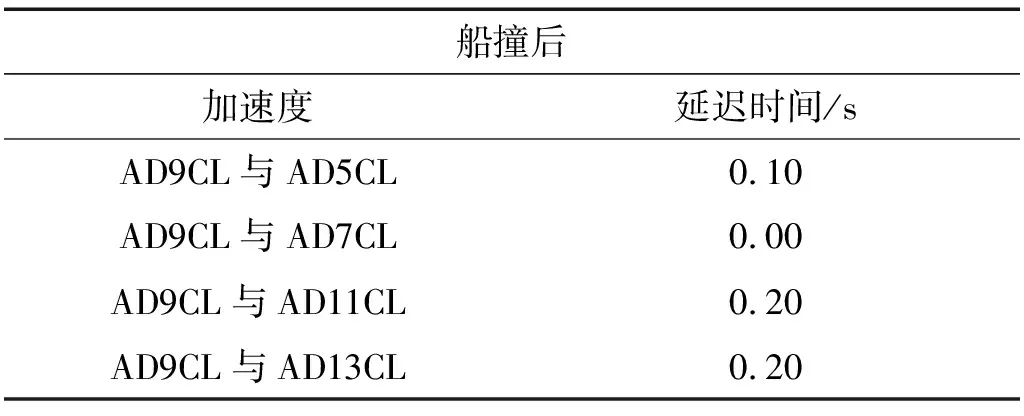
表4 船撞后实测加速度间的时间延迟

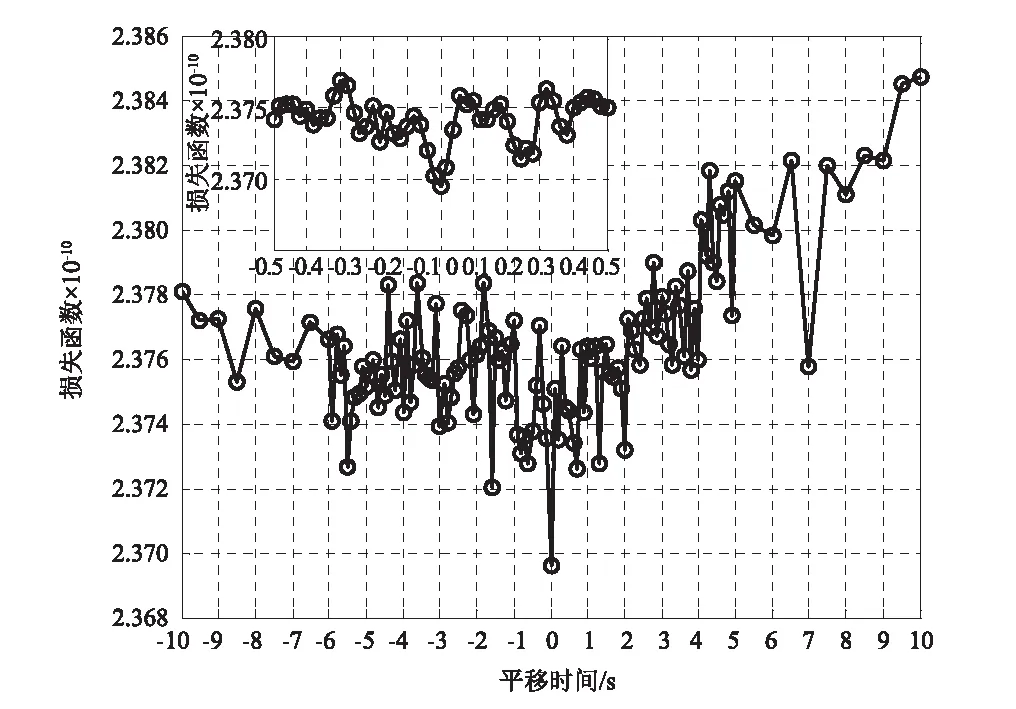
图11 损失函数随平移时间的变化图(船撞后的加速度AD9CL与AD7CL)Fig.11 Loss function versus shifting times for acceleration AD7CL measured after ship-bridge collision

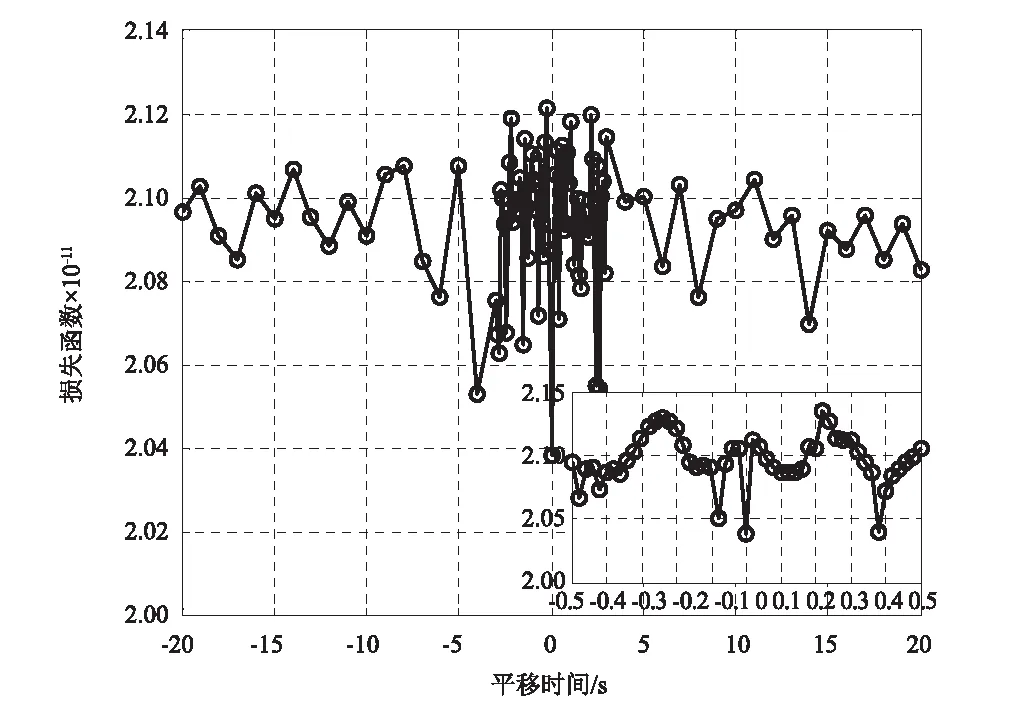
图12 损失函数随平移时间的变化图(船撞后的加速度AD11CL与AD13CL)Fig.12 Loss function versus shifting times for acceleration AD11CL measured after ship-bridge collision

4 结 语

本文对江阴大桥船撞期间的实测加速度数据进行了时间同步研究。采用状态空间模型方法识别不同位置处加速度间的时间延迟。以一个参考信号和一个时间平移信号为输出变量，构建状态空间模型。状态空间模型的最优阶数由AIC与FPE确定，并使用损失函数评价模型的预测能力。对每一对参考信号与时间平移信号，分析了一系列的平移时间所对应模型的损失函数，损失函数到达最小值时所对应的平移时间则认为是实测加速度之间的实际时间延迟。此外，本文还对船撞前后的实测加速度进行了研究，以全面评估状态空间模型用于时间同步分析的性能。船撞前的异步加速度数据用于评估状态空间模型方法的可重复识别能力及精度，船撞后的同步加速度数据则用于测试状态空间模型方法的防伪识别能力。通过研究，可得出以下结论：

(1)状态空间模型可成功识别船撞期间的实测加速度之间的时间延迟。实测加速度中的船撞事件验证了状态空间模型方法所确定的时间延迟的正确性，而且时间同步的加速度数据则验证了状态空间模型方法的抗伪识别能力。

(2)状态空间模型方法成功识别了船撞前的实测加速度之间的时间延迟，说明它能在没有任何显著事件的帮助下识别加速度之间的时间延迟。在大多数实际应用中，监测数据往往不存在已知的显著事件，状态空间模型在这种情况下能够识别异步数据的时间延迟，进一步验证了该方法的有效性。

(3)总体而言，状态空间模型方法的时间同步精度是可接受的。船撞前与船撞时所识别得到的时间延迟的最大差值为0.28 s。值得注意的是，由于结构健康监测系统还未进入正式运营，此时的监测数据可能引入了更多的不确定性，这都可能影响状态空间模型方法的时间同步精度。

(4)状态空间模型在识别同步数据的延迟时间时也取得了令人满意的性能。部分加速度识别得到延迟时间为零，而且加速度的延迟时间与真实延迟时间的最大偏差为0.20 s。因此，总体上状态空间模型的抗伪识别能力是令人满意的。