热耗散变形下干气密封角向摆动稳定性的研究

张伟政， 席喜林， 李水平， 陆俊杰， 丁雪兴

(兰州理工大学 石油化工学院，兰州 730050)

干气密封是一种新型的密封形式，其中常用的螺旋槽干气密封有低泄漏、低功耗、长寿命和高稳定性等优点，在化工机械设备上得到了广泛的应用，同时引起了国内外专家学者的研究兴趣[1-2]。干气密封是一种非接触式机械密封[3]，动静环两端面间会形成一层厚度为3～6 μm 且具有一定刚度的气膜，使得密封环端面不发生接触，保持稳定运行。若间隙发生微小变化，极有可能使密封端面接触摩擦，产生热力变形，划伤和磨损，严重时甚至发生干气密封失效。因此，有必要对干气密封的稳定性进行深入研究。

近几年，国内外专家学者先后做了大量的工作。Zhang等[4]考虑了3个自由度下的干气密封振动模型，建立了微扰运动方程，获得了密封环的动态特性。Thatte等[5]研究了超临界CO2涡轮机械设备用干气密封的运行情况，计算极坐标下可压缩雷诺方程获得动静环之间的气膜刚度变化特性。Lee等[6]利用有限元的方法求解了螺旋槽干气密封在非稳定状态下的气膜承载力、气膜压力和泄漏量等变化规律。Kollinger[7]通过试验测试了轴向振动对一个稳定气体润滑机械密封的影响。Miller等[8]分析了螺旋槽端面在轴向和角向上的密封环运动，使用直接数值的频率响应方法和瞬态雷诺方程，求得了相关的气膜刚度与阻尼特性。Zhou等[9]搭建试验台，研究了非接触螺旋槽机械密封的磁流体薄膜的润滑特性，获得密封承载力与外部磁场强度的关系。丁雪兴等[10-11]对3种不同螺旋角的螺旋槽干气密封气膜振动位移进行测量，分析了其稳定性，并建立轴向密封系统振动模型求解失稳域范围。张伟政等[12]建立了角向振动下气膜-密封环系统模型，获得了密封系统稳定时的结构参数区域。刘蕴等[13]利用ANSYS Workbench软件对螺旋槽型干气密封系统的动力学特性进行分析，解释了振动趋势形成的原因。刘占生等[14]建立浮环密封和转子瞬时运动关系，基于有限元单元法求解瞬态流体压力并考虑了失稳现象。

学者们从机理、数值计算、测试等多方面分析了密封动态特性和稳定性，但是考虑微尺度热耗散以及变形对干气密封系统动态稳定性的影响还相对匮乏，尤其在角向摆动问题上。

本文考虑非线性振动、微尺度效应和热耗散变形的影响，研究螺旋槽干气密封系统角向振动问题，分析干气密封稳定运行的螺旋角范围。同时，通过试验观察不同螺旋角对端面的影响，从而判断热耗散变形下的螺旋角范围对干气密封稳定运行的影响。

1 干气密封理论计算的分析模型

1.1 干气密封的工作原理

图1所示为干气密封常见的结构形式—双端面(背靠背)。双端面干气密封主要由弹簧、弹簧座、静环、动环、动环轴套、O形圈和密封腔构成。气体从密封腔通入干气密封，动环表面开设了微米级的螺旋槽，同时在转速和压力的作用下，气体在螺旋槽内压缩形成动压效应，并且在静环背压和弹簧的作用下达到力平衡，使得动静环两端面之间被推开形成一层3～6 μm的气膜刚度。

1.2 物理模型

干气密封密封环之间的气膜可以看做窄缝间的气体流动，动环和静环是窄缝的上下端面，同时3～6 μm窄缝需要考虑气体的稀薄效应[15]。根据流体在窄缝中流动的特点，结合气膜密封的特殊之处，作出以下基本假设：

(1)等温，等黏度；

(2)气体为理想气体；

(3)气体作层流运动；

(4)忽略气体的惯性力与体积力；

(5)气膜流速进入滑移区。

1.3 几何模型

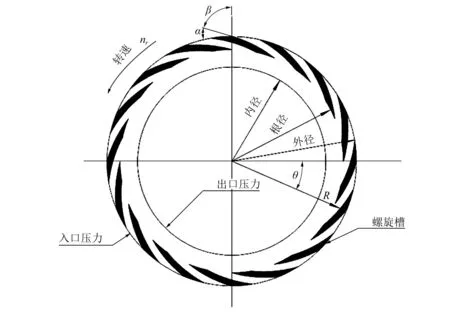
图2 密封动环螺旋槽结构Fig.2 Schematic of the spiral groove

图2为螺旋槽干气密封动环，螺旋槽由对数螺旋线构成，并且周向分布。气体利用微尺度槽道的动压效应形成气膜力，影响螺旋槽动压效应的有以下三个关键参数：槽数、螺旋角、槽深，三个参数控制着螺旋槽的压力、刚度、稳定性、泄漏量等一系列密封特性[16]。利用光纤激光打标机对动环表面进行加工，螺旋槽为槽区，非槽区称为密封台区，图中Ro是密封环外半径，Ri是密封环内半径，Rg是密封环根半径，α是螺旋角，β是螺旋角的余角，n为槽数，2E是螺旋槽槽深。

1.4 数学模型

干气密封气膜理论的基础是流体力学,其控制方程是纳维-斯托克斯方程。根据干气密封几何模型和速度滑移，气膜的二维雷诺方程：

(1)

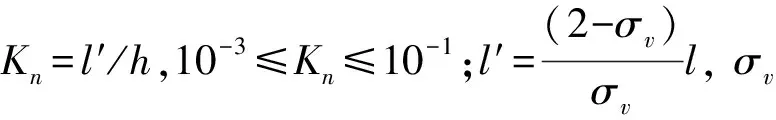
根据1.2节的假设和理想气体状态方程，可将式(1)写成：

(2)

为了便于后续的理论分析，将式(2)进行无量纲，获得了无量纲下的雷诺方程：

(3)

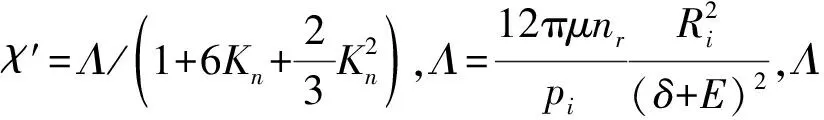
2 干气密封相关基本方程的建立

2.1 振动方程

根据干气密封的工作原理，对图3所示的角向摆动模型提出以下假设：

(1)气膜与密封环在运行中都具有振动位移变化，因此将振动模型设定为双自由度；

图3 角向摆动模型Fig.3 The model of angular vibration

(2)气膜具有一定的刚度，因此将气膜转换成具有非线性刚度的弹簧；

(3) 动环跟轴共同旋转，其位移设定为简谐运动。

振动方程：

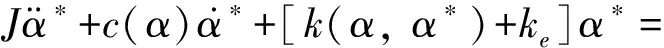
(4)

2.2 热耗散下的气膜能量方程

图4为气膜微元体热量传导模型。稳态下，由对流换热过程控制方程组推导气膜的能量方程[17]。

图4 气膜微元模型Fig.4 A micro control element

则微元体在单位时间内由扩散所吸收的热量为：

(5)

单位时间内控制体由对流作用得到的热量为：

(6)

由于膜厚间隙相当小，所以dz向的能量主要以扩散形式进出气膜。则在单位时间内由扩散所吸收的热量为：

(7)

同时将流体黏性耗散作用所产生的热量加入气膜微元体[15]，根据能量守恒定理，最终气膜的能量方程：

(8)

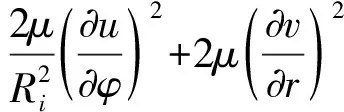
忽略温度在气膜厚度z方向变化,则气膜的能量方程式(8)简化为：

(9)

忽略耗散项，得到不考虑热耗散下的气膜能量微分方程：

(10)

2.3 气膜厚度方程

干气密封的动环采用SiC材料，静环采用石墨材料。配对方式：硬环对软环。在不同温度和压力下，动环的变形量远小于静环的变形量。因此，在进行变形计算时，只考虑静环变形，动环变形忽略不计。

干气密封静环轴向热弹变形为[18]：

δta=aLbfCR

(11)

式中：L为密封环长度;bf是密封面宽度;a是线膨胀系数；CR=ΔT/bf是温度梯度。

干气密封运转下，若静环无变形时，密封端面间的气膜厚度均厚定值hb；但是当静环发生变形时，气膜厚度hb为变量，其表达式为：

hb=hmin+Δ=hmin+δmax-δ

(12)

式中：δmax为静环变形最大值，hmin为气膜厚度最小值，如图5所示。

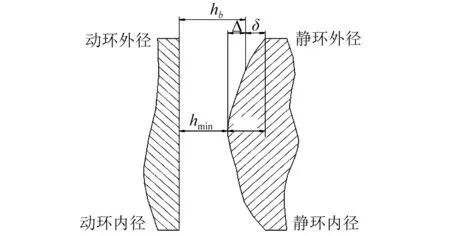
图5 气膜厚度结构简图Fig.5 The structural diagram for the gas film thickness

利用PH线性化方法和复函数分离变量法，将式(3)变为线性微分方程；随后采用迭代法近似求解方程[19]，获得气膜开启力：

(13)

静环由于热耗散发生了变形，均厚下的气膜变为了两头宽中间窄，从而打破了干气密封原有的平衡状态，根据工作原理，气膜开启力Fo等于密封闭合力Fc：

Fo=p0A+Fe

(14)

式中：A为静环面积(m2)，Fe为弹簧力(N)。

3 密封系统稳定性分析

3.1 计算实例

应用PH线性法和变分法，得到了角向位移微扰下的气膜反作用力的增量，再利用复变函数和迭代法对气膜边值问题进行求解。由于角向微扰量为复数(K=η(η1(ζ)+η2(ζ)i)e-iω)，所以雷诺方程的微扰动态压力是复变量，其实部和虚部就分别对应了气膜的刚度和阻尼[20]。

微扰动态压力的复数实部Re{K}=η(η1cosω+η2sinω)得到无量纲气膜刚度的计算式：

(15)

微扰动态压力的复数虚部Im{K}=η(-η1sinω+η2cosω)得到无量纲阻尼的计算式：

(16)

式中：

由此，气膜角向摆动刚度：

(17)

阻尼：

(18)

表1为螺旋槽结构参数，表2为运行工况参数。

表1 螺旋槽结构参数

表2 运行工况参数

联立(13)和(14)，得到气膜的最小厚度为3.82 μm。将气膜厚度进行逐段计算，分别得到含有气膜非线性刚度和阻尼的两个多项式。由于影响非线性气膜刚度的因素较多，忽略密封加工和安装误差，和旋转设备自身问题，只考虑结构参数对其影响，而螺旋角是体现对数螺旋线和控制线型方向的关键参数。所以对振动敏感参数螺旋角作为变量来研究分岔问题。

拟合气膜非线性刚度：

K*=(α×0.291 069×1018-0.379 745×1018)×x2+
(α×0.234 142×1014-0.305 479×1014)×x-
(0.821 755×109+α×0.629 844×109)

(19)

拟合气膜非线性阻尼：

Cg=(-α×0.585 365×1017+0.774 43×1017)×x2+
(-0.469 328×1013×α+0.620 945×1013)×x-
α×0.125 762×109+0.166 398×109

(20)

3.2 Floquet指数法对方程化简求解

将式(19)、 (20)代入式(4)中，两边同除以J得：

(21)

式中：

c0=c/J,

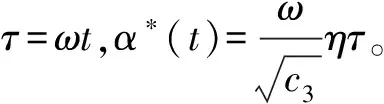
则方程变为：

(22)

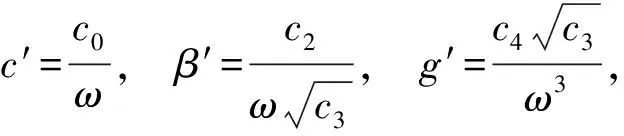
简化得：

(23)

其中：

(24)

3.3 热耗散变形下的分岔问题的螺旋角范围

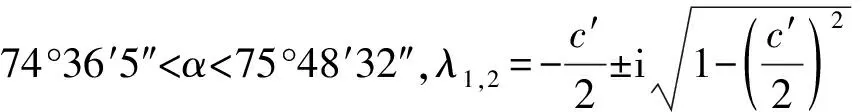
当c′=2时，α=74°36′5″时，λ1,2=-1为相等的负数，平衡点为临界结点。

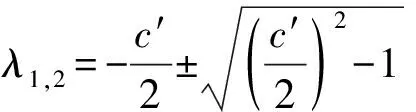
当c′=1时，α=75°48′32″时，λ1,2=±i为纯虚数，解的曲线是极限环，如图6所示，说明螺旋槽干气密封发生Hopf分岔。

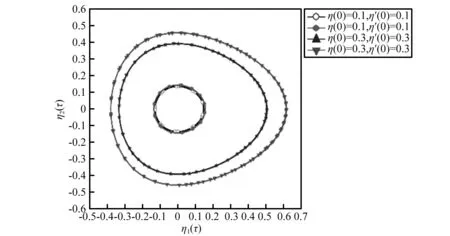
图6 相图Fig.6 Phase plane

以上针对干气密封系统的稳定性进行了分析，当螺旋角74°36′5″<α<75°48′32″范围内，干气密封系统是稳定运行的，当螺旋角为α=74°36′5″和α=75°48′32″时，是干气密封系统稳定运行的临界点。当螺旋角α<74°36′5″或α>75°48′32″情况下，系统运行将会不稳定。

3.4 无热耗散变形下的分岔问题的螺旋角范围

当c′=2时，α=74°39′37″时，λ1,2=-1为相等的负数，平衡点为临界结点。

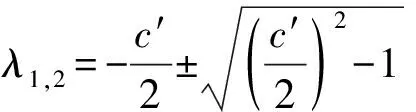
当c′=0时，α=75°42′55″时，λ1,2=±i为纯虚数。解的曲线是极限环，发生Hopf分岔。

对比有无热耗散变形下的计算结果发现：热耗散变形下发生分岔问题的螺旋角范围比无热耗散变形广；同时，分岔点位置要比无热耗散变形下更大。这种螺旋角失稳域的变化，说明考虑热耗散下气膜-密封环流固耦合系统稳定性研究对螺旋槽干气密封的稳定运行和优化指导具有重要作用。

4 试验测试与分析

4.1 测试系统

本次试验的测试系统分为四大系统：传动系统、供气系统、测试系统和密封系统，如图7所示。

图7 测试系统台Fig.7 Photograph of the test bench

传动系统由电机、轴承箱、主轴等组成， 0～10 000 r/min范围内自由调控。供气系统由流体无缝钢管、压力表、流量计、溢流阀等组成，使用范围为：0～15.0 MPa。测试系统由传感器、信号调理模块、数据采集卡、计算机、软件等组成，监控密封系统的工作状态。干气密封测试系统的原理图如图8所示。密封系统由双端面干气密封组成，采用双端面干气密封目的在于便于拆装，避免对动静环表面造成损伤。

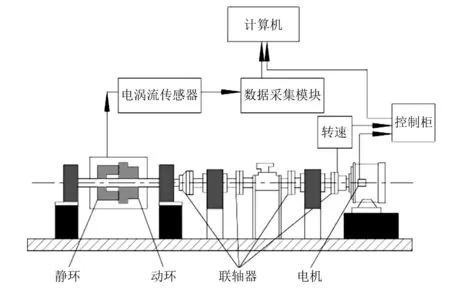
图8 测试原理图Fig.8 Schematic drawing of test bench

4.2 测试原理

采用常州双环厂生产的金属管浮子流量计LZZ-15/1/RR1/A/M1对泄漏量进行测量。通过气路系统对密封端面进行通压，并通过减压阀保持压力恒定，进气补充气量为端面泄漏量。

本次试验采取表1中的参数，对密封环进行加工，动环采用SiC材料，静环采用石墨材料。动环的结构根据螺旋角的角度差异而有所不同，螺旋角的选定依据来自于文中热耗散变形下的螺旋角数值。两个动环螺旋角分别设定75°50′为(非稳定下的螺旋角数值)，75°(稳定下的螺旋角数值)；两个静环的结构尺寸保持一致(分别为1号静环和2号静环)。选用的试件为干气密封的“软碰硬”结构，相对于“软环”石墨环，“硬环” SiC环的硬度要远大于石墨环，在试验的过程中，SiC环的表面基本保持不变，可以忽略不计，故本次试验只讨论螺旋槽与石墨环表面的关系。

具体试验步骤：

(1)将动静环进行加工、刻槽、去毛刺飞边、抛光、清洗和烘干，随后进行装配。75°50′动环与1号静环配对，75°动环与2号静环配对，准备两套干气密封双端面样机(1号样机和2号样机)。

(2)在实验台上安装1号样机，先往密封腔通入压力，随后进行盘车，确认无误后，启动电机进行升速，将压力稳定在10.0 MPa，转速稳定在10 000 r/min，观察压力表和流量计的变化。

(3)1号样机运行30 min后，先停止转速，再关闭压力，将1号样机进行拆卸，观察静环的表面变化情况。

(4)对试验台安装的密封腔进行吹扫后，安装2号样机，操作步骤如同(2)和(3)。

(5)1号静环和2号静环对比分析，观察两者的端面 程度和泄漏量随时间变化规律。

4.3 测试分析及对比

图9为1号静环端面，图10为2号静环端面。从两张图中能直观得看到，1号静环表面有严重的擦痕，甚至出现了磨损。擦痕呈周向均匀分布，区域恰好对应动环的槽区(外径至根径)，并且中间的擦痕更为明显；2号静环表面较为光整，看不出明显的擦痕现象。

静环表面擦痕的发生说明干气密封的工作状态是非平衡状态；同时，擦痕分布的区域正是动环螺旋槽的动压效应区，两端面间没有保持一层稳定而有效的气膜刚度，使得动静环的角向摆动变得更加剧烈，气体在端面和槽区的运动加剧，从而导致动环和静环在运行的过程中，会有间断的碰撞和摩擦。另外，静环端面中部的擦痕最为明显，说明热耗散下静环发生了变形由于气膜变为中间窄两头宽的形状。所以，在不稳定的气膜刚度、角向摆动和变形的共同作用下，对静环表面造成了严重的伤害。

图11为螺旋家75°50′和75°的干气密封泄漏量，从两者的泄漏量可以直观的看到：75°的干气密封在前10 min逐渐上升，随后保持一个稳定的泄漏量数值，这是由于在刚开始运行的过程中螺旋槽干气密封逐步脱开，密封间隙变大导致泄漏量增加，但是当气膜开启力和闭合力稳定时，气膜刚度保持动态平衡使得泄漏量控制在一个稳定的数值，不存在稳定性下降和泄漏量增加的可能。但是，相比较75°50′的干气密封，在运行的30 min内泄漏量不断增加，从前期的缓慢增加到后期的急剧上升说明螺旋槽干气密封发生了失稳导致泄漏量不断上升，影响密封设备和旋转机械的正常工作，造成此种现象的原因：螺旋角为75°50′的干气密封在运行过程中，容易发生失稳，导致动静环端面碰撞和变形，影响气膜结构，导致泄漏量的不稳定性。起初运行时，端面的擦痕不明显，造成的损伤较小，但是随着运行时间的增加，端面擦痕和气膜变形越来越严重，导致泄漏量上升速率增加。

若长时间运行，必定刮伤动环的槽区，导致泄漏量增大，严重时，将会降低干气密封的使用寿命，出现安全问题。因此，考虑热耗散变形下的螺旋角范围，对干气密封稳定性有一定程度的影响，说明了理论计算的准确性。在工程实际应用领域中，应尽量避免选择出现密封系统分岔的螺旋角区域。

图9 1号静环端面图Fig.9 No. 1 static ring face

图10 2号静环端面图Fig.10 No. 2 static ring face

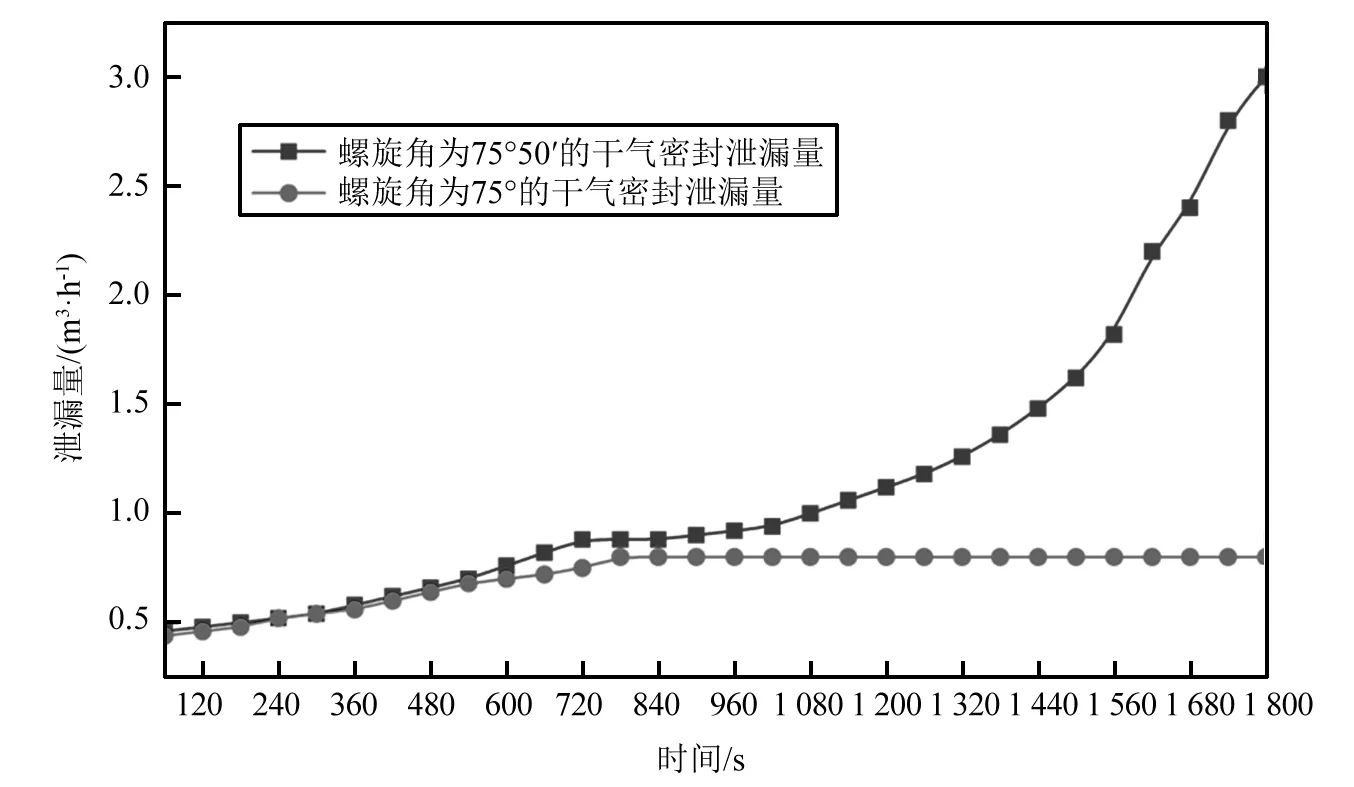
图11 不同螺旋角的泄漏量随时间变化Fig.11 Leakage of different spiral angles with time

6 结 论

本文考虑热耗散变形研究螺旋槽干气密封系统角向振动的稳定性问题，分析干气密封系统发生分岔和稳定运行的螺旋角范围，并且结合试验分析，得到了如下结论：

(1)建立密封环双自由度的振动方程，结合Floquet指数，求解了螺旋槽干气密封发生失稳的螺旋角数值。耗散变形下的螺旋角为75°48′32″，无热耗散变形下的螺旋角为75°42′55″，说明干气密封系统发生分岔的位置有明显变化，热耗散对干气密封的运行有一定的影响。

(2)从干气密封稳定运行的螺旋角范围来看，热耗散变形的螺旋角范围(74°36′5″<α<75°48′32″)相比较无热耗散变形条件下的螺旋角(74°39′37″<α<75°42′5″)的区域更加明显，说明对干气密封螺旋角的选择，需要考虑热耗散对其影响。

(3)试验表明了75°50′的干气密封端面发生擦痕，而75°的密封端面保持光整，同时通过对比两个不同螺旋角下的干气密封泄漏量，可以发现75°50′下的泄漏量随着擦痕的严重程度而不断增加，而75°下的泄漏量在一段时间以后保持在稳定的数值，证明了考虑热耗散变形对干气密封系统的稳定性有一定的影响，从而验证了理论计算的准确性。因此考虑热耗散变形下密封动态稳定性的研究对工程实际有指导意义。

(4)今后研究干气密封系统角向振动问题时，需耦合激振力或考虑外部存在激励的情况，令计算结果更加精确，更加符合实际工程应用。