非接触机械密封端面间流体膜流动状态临界雷诺数的讨论*
2019-08-02
(昆明理工大学化学工程学院 云南昆明 650500)
非接触机械密封一般是指气体润滑的气膜密封(干气密封)和液体润滑的上游泵送机械密封(液膜密封),它们已在工业上获得广泛应用[1-4]。在该类机械密封的设计、研究和应用过程中,一般认为密封端面间的流体膜流动是处于层流状态[5];但在转速较高、流体膜厚度较大或被密封流体的压力较高时,端面间流体膜的流动状态可能进入湍流状态。层流和湍流是2种完全不同的流动状态,由于密封端面间流体膜的流动是属于包含压差流和剪切流在内的一种复合流动,如何判断压差剪切复合流动从层流到湍流的转捩是一个尚未解决的问题。对于单纯的压差流或剪切流,目前已有很多研究。一般可依据临界雷诺数进行判断,当雷诺数大于临界雷诺数时,流动状态即处于湍流状态,而临界雷诺数的具体数值目前只能通过实验确定。对于压差剪切复合流动,目前虽然也有一些研究,但尚未形成共识。本文作者梳理压差流、剪切流、复合流的临界雷诺数相关文献并进行分析对比,提出采用一种复合速度法,即利用复合速度来确定压差剪切复合流动临界雷诺数。研究表明,采用该方法可判断压差剪切复合流动是否处于湍流状态。
1 压差流动的临界雷诺数
1.1 圆管压差流动
1.1.1 雷诺数的定义
自然界中流体流动通常分为层流和湍流2种形式。Reynolds最早开展流体在圆管中流动的实验研究,发现了流体从层流向湍流的转捩,并给出了判别流动状态的参数——雷诺数(Re)。对于不同的流体流动,雷诺数有不同表现方式,而这些表现方式一般都包括流体性质(密度、黏度)、流体速度以及一个特征长度或特征尺寸。其中特征长度或特征尺寸一般根据习惯定义。对于管内流动,通常使用直径作为特征尺寸。
对于在圆管内的压差流动,雷诺数定义为
(1)
式中:v为管内流体流动的平均速度(m/s);D是管子的内直径(m);μ是流体动力黏度(Pa·s);ν是运动黏度(ν=μ/ρ,m2/s);ρ是流体密度(kg/m3);Q是体积流量(m3/s);A=πD2/4,为横截面积(m2)。
1.1.2 液体流动
普通圆管中由压差驱动的液体流动,从层流到湍流的临界雷诺数Repc在1 800~2 300之间[6]。一般计算时,临界雷诺数取Repc=2 000。而对于微管或者其他形状的截面的微通道,流体流动的临界雷诺数并不统一。MAYNES和WEBB[7]研究了直径为705 μm的微管中水的流动,发现当Re>2 100时,发生湍流行为。SHARP和ADRIAN[8]研究了直径为50~247 μm的玻璃微管中不同极性的液体从层流到湍流的转捩,发现湍流发生在雷诺数Re=1 800~2 200之间,与宏观管流的一致。LI等[9]采用直径79.9~166.3 μm的玻璃管,100.25~205.3 μm的硅管和128.76~179.8 μm的不锈钢管,研究微管中去离子水的流动特性,发现在光滑微管中,水的临界雷诺数Re=2 000~2 300,而在粗糙微管临界雷诺数Re=1 700~2 000,这说明粗糙度对微管中流体的临界雷诺数有不小的影响。WU和CHEN[10]用光滑的梯形微通道,研究水力直径D=103.4~291.0 μm范围内流体从层流到湍流转捩的临界雷诺数,发现梯形截面微通道中的临界雷诺数Re=1 500~2 000。HETSRONI等[11]分析了水力直径为1.01~4 010 μm的圆形、矩形、三角形和梯形微通道压差流动的影响,发现流体在直径大于50 μm的微管中,与宏观流动没有区别。
对于光滑和相对粗糙度在0.32%~7%范围内的微通道,流体从层流到湍流过渡的雷诺数Re=1 800~2 200。在雷诺经典管流实验中,雷诺提出并确定了层流、紊流和临界雷诺数,并以圆管中压降与雷诺数的关系确定判断管流流态的准则[12],采用临界雷诺数为2 000,以区分层流和紊流。所以对于微管或者微通道压差液体流动,判断流动状态的临界雷诺数仍然可以采用经典值Rec=2 000。
1.1.3 气体流动
关于气体流动的临界雷诺数,研究的人相对较少。YANG等[13]以空气为介质在直径为173~4 010 μm的管内研究了气体流动的临界雷诺数,发现空气在微管中从层流到湍流的过渡雷诺数Re=1 200~3 800。黄迦乐等[14]以氮气为工作介质在直径为20~50 μm的微石英管内对气体流动特性进行实验研究,发现当Re>2 300时,流体进入紊流状态。所以对于微管或者微通道气体压差流动,判断流动状态的临界雷诺数仍可以采用常用值Rec=2 000。
1.2 套管压差流动
将套管沿圆周方向展开即近似为平行平板。因此,可用套管压差流动来近似平行平板间的压差流动。而流体沿密封端面间的径向压差流又可用平行平板间的压差流来近似。目前关于流体在套管中流动特性的研究不多,其雷诺数的定义和临界雷诺数的资料很少。一般以水力当量直径作为特征尺寸定义雷诺数。径向间隙为h,外管内直径为d2,内管外直径为d1的套管示意如图1所示。流体在间隙为h的环形空间内由压差驱动沿套管的轴向流动。
套管的流体流通面积为
(2)
润湿周边长度为
L=π(d2+d1)
(3)

图1 套管结构示意图
根据水力当量直径的定义,流体在圆形套管内流动的水力当量直径:
(4)
根据圆管雷诺数定义的表现形式,可将套管流动的雷诺数定义为
(5)

一般认为,计算流动阻力时,按水力当量直径确定的雷诺数等价于圆管内流动的雷诺数。因此可以认为,按式(5)计算的套管或平行平板间压差流的临界雷诺数与圆管流动相同,即Retpc=2 000。
关于套管或平行平板间流动的流型转变的实验研究很少。孙月秋等[15]在研究水在套管中的流动传热特性时,将雷诺数按虚拟的流体流动速度确定,即
(6)

式(6)的形式和圆管雷诺数式(1)的形式相同。但值得注意的是,式(6)中的流体平均速度u不是真实的平均速度,而是根据套管平均直径计算的一个虚拟的平均速度。从式(6)和式(5)可以看出,Res=2Retp,即按虚拟平均速度定义的雷诺数Res是按物理概念定义的雷诺数Retp的2倍。孙月秋等[15]的实验研究表明,水在套管中流动,从层流到湍流转捩的虚拟流速概念的雷诺数Res=2 000~3 000,相当于物理概念雷诺数Retp=1 000~1 500。但他们的实验也表明,从层流到湍流转捩的雷诺数受套管间隙的影响。
2 剪切流动的临界雷诺数
2.1 平行平板间的剪切流动
2.1.1 剪切雷诺数定义
将套管沿圆周方向展开即近似为两平板,套管间隙h即为两平板间间隙。类似地,平板间间隙为h的剪切流的水力当量直径De=2h,仿照压差流,平板间间隙为h的剪切流的雷诺数定义为
(7)
式中:v为剪切流的平均速度。
假设一个平板静止,另一个平板移动速度为U,对于牛顿流体,其剪切流的平均速度为
(8)
将式(8)代入式(7)得到剪切流常见的雷诺数定义式:
(9)
对于旋转的轴与轴承之间间隙形成的剪切流,其雷诺数的定义式为
(10)
式中:ω为旋转角速度;r为轴的半径。
式(9)和式(10)是常见的剪切流的雷诺数定义式,其本质与压差流的雷诺数定义式一致。
值得注意的是,在某些剪切流动的实验研究[17]和理论研究[18]中,流动模型如图2所示,其雷诺数定义采用一半速度与一半间隙,即:
(11)
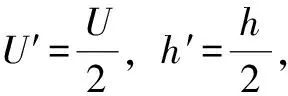
(12)
即半速半间隙定义的雷诺数Reτh是常规雷诺数Reτ的1/4,或者说常规雷诺数Reτ是半速半间隙雷诺数Reτh的4倍。
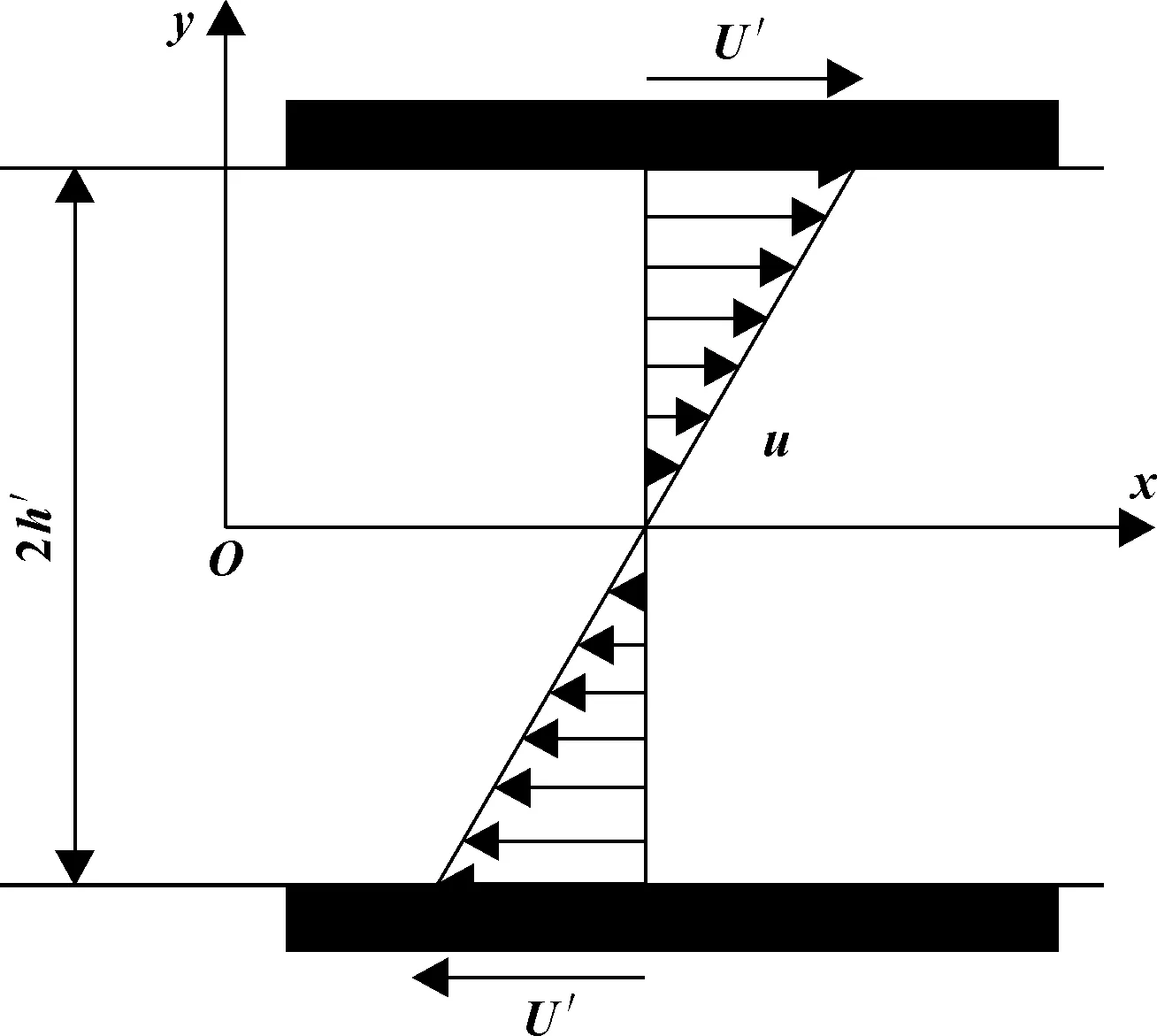
图2 两平板双向运动剪切流的模型示意图
2.1.2 平板剪切临界雷诺数
关于平板剪切流动临界雷诺数的研究不多,其数据并不一致。TAYLOR和DOWSON[16]的研究采用常规剪切雷诺数Reτ,通过实验观察到平板库埃特流动的临界雷诺数Reτc=1 900。TILLMARK和ALFREDSSON[17]的实验研究,采用半速半间隙定义雷诺数,实验得到能够维持湍流的最低雷诺数为360±10,相当于常规雷诺数为1 440±40,其两平板为双向流动。DOU和KHOO[18]运用能量梯度法来解释流体从层流到湍流的流动机制,采用半速半间隙定义雷诺数,其理论研究和实验研究认为,临界雷诺数均为370,相当于常规临界雷诺数为1 480。
2.2 同心圆筒间隙间的剪切流动
2.2.1 泰勒涡
流体在同心圆筒间隙中的周向剪切流动,是由于内外圆筒相对旋转运动而产生。随着相对转速的增加,这类流动首先出现的非层流是泰勒涡,可用临界泰勒数加以判断。泰勒涡是层流失稳后形成的一种二次流。经过泰勒涡后才是常规意义上的完全湍流。一般情况下,临界泰勒数[12]为
(13)
对于一般的圆柱间隙剪切流,判断出现非层流状态的临界雷诺数为
(14)
式中:c=R2-R1,为半径方向的间隙;R根据情况,可取内圆柱半径R1(内筒旋转),或外圆柱的内直径R2(外筒旋转),或平均直径Rm=(R2+R1)/2;U为圆筒旋转的线速度。
2.2.2 临界雷诺数

荣深涛等[20]在同心环隙库特流层流解析解及实验验证的研究中观察到,当雷诺数达到2 000时开始出现紊流,作者认为可以把Re=2 000作为临界雷诺数。
3 压差剪切复合流动的临界雷诺数
3.1 复合速度法
利用矢量复合速度作为特征速度来计算雷诺数是一种合理的构想。李邦达和刘永建[21]在偏心环空中幂律流体层流螺旋流流动的稳定性的研究中也采用了矢量合成速度的方法来计算稳定性系数H。
根据压差流临界雷诺数Rep=2 000,剪切流临界雷诺数Rec等于2 000或接近2 000的现象,针对压差剪切复合流动,利用压差流形成的速度与剪切流形成的速度之矢量和,即复合速度矢量,作为雷诺数的特征速度,依此计算复合流动的雷诺数ReM,并以临界复合速度雷诺数ReMc=2 000作为出现湍流的判据。即
(15)
或者
(16)
式中:De为特征尺寸,对平行平板或同心圆筒(套管),De=2h;Um为压差流和剪切流形成的复合速度(矢量和),如果压差流的速度Up和剪切流的速度Uc垂直,则复合速度
(17)
式(15)或(16)物理概念清晰,计算简单、实用。
对于压差流的速度Up和剪切流的速度Uc相互垂直的情况,复合速度雷诺数式(15)和雷诺数复合的复合雷诺数等效。雷诺数复合的复合雷诺数可以定义为
(18)
式(18)与式(15)相同,即以复合速度计算的复合雷诺数与以雷诺数复合计算的复合雷诺数是一样的。
3.2 流动因子复合雷诺数法
BRUNETIERE等[22]应用流动因子α来表达复合流动的复合雷诺数概念,流动因子定义为
(19)
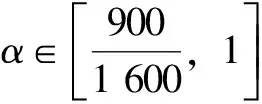
式(19)的本质是认为压差流的湍流临界雷诺数Repc=2 300,剪切流的湍流临界雷诺数Rectc=1 600,剪切流的层流临界雷诺数Rectl=900。即对于纯剪切流,当雷诺数Rec<900时为层流,当雷诺数Rec>1 600为湍流,当雷诺数Rec∈[900,1 600],流动既非层流,也非湍流,是一种类似于泰勒涡的非稳定二次流。流动因子法得到了广泛应用[23-26]。
如果取临界雷诺数Repc=2 000,Recc=2 000,则相应的流动因子为
(20)
临界流动因子
(21)
即αMc>1时,复合流动处于湍流状态。可以看出,式(15)、(16)、(18)复合速度法与BRUNETIERE的流动因子法(式(19))一致。文中的复合速度法仅区分湍流和层流,即超过临界复合雷诺数ReMc=2 000或临界流动因子αMc=1即为湍流,否则为层流。
4 密封端面间流体流动状态的判断
机械密封端面间的流体流动为典型的压差流和剪切流垂直的复合流动。下面以干气密封为例,说明如何利用复合速度法和流动因子法对流体的流动状态进行判断。
以GABRIEL[27]提供的螺旋槽干气密封的几何尺寸和运行条件为例进行分析。
几何尺寸为:Ro=77.78 mm,Ri=58.42 mm,Rg=69 mm,α=15°,γ=1,hg=0.005 mm。
操作条件为:po=4.585 2 MPa,pi=0.101 3 MPa,平均直径处线速度u=74.03 m/s,相当于角速度ω=1 087.08 s-1或转速n=10 380.8 r/min。
根据宋鹏云[28]计算气膜压力的方法,可计算出密封坝各半径处的压力,根据相邻两点的压力差,即可计算出泄漏率对应的各点的径向速度。越靠近出口,气体的径向速度越大。以紧靠出口,半径为58.684 5 mm处的径向速度作为密封坝区的最大速度。不同膜厚下,该半径处的密封坝区最大的径向速度vi如表1所示。

表1 密封端面槽根的气膜压力、径向速度
对应半径58.684 5 mm处的周向速度为ui=63.794 6 m/s,在此状态下,根据式(15)、(17)、(18)计算的复合速度(Um)和复合雷诺数(ReM)如表2所示。

表2 密封端面坝区的复合速度和复合雷诺数
密封端面坝区径向的雷诺数ReP和周向雷诺数ReC分别如表3所示。
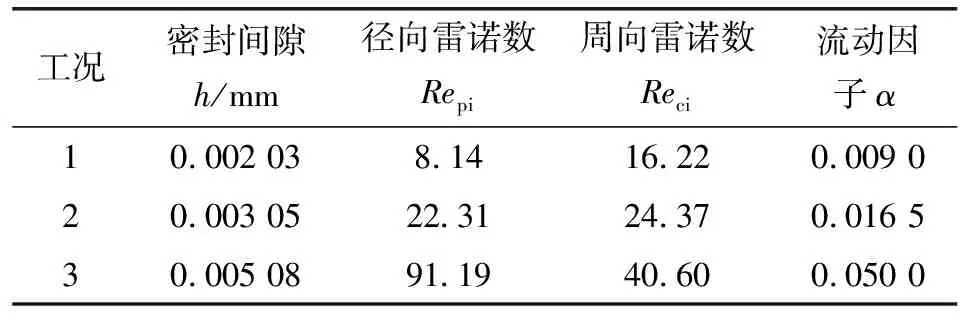
表3 密封端面坝区的径向雷诺数和周向雷诺数
根据式(20)、(21)计算的3种工况下的复合雷诺数ReMi分别为18、33、100,且α=ReMi/2 000均小于1,即为层流。
5 结论
(1)提出一种利用复合速度计算压差剪切复合流动雷诺数的方法,即将压差流与剪切流形成的速度的矢量和作为雷诺数的特征速度来计算雷诺数,简称复合速度雷诺数,并以复合速度雷诺数等于2 000作临界雷诺数判据,来判断流体膜的压差剪切复合流动是处于层流状态还是处于湍流状态。
(2) 以GABRIEL经典论文数据为例,利用复合速度方法得到的最大复合雷诺数为100,小于复合流动临界雷诺数,处于层流状态。结果表明,可应用复合速度雷诺数或复合雷诺数或流动因子α对 流动状态进行判断。
(3)文中提出的复合速度法仅为近似估算方法,更严格的方法应按流体稳定性理论确定。
