基于小波能量谱的T型线路故障定位新算法*

汪 梅， 朱 亮， 张国强， 王 亮， 刘 驰

(1. 西安科技大学电气与控制工程学院 西安，710054) (2. 北京理工大学软件学院 北京，100081)

引 言

T型输电线路具有线路结构简单、施工速度快以及能够减少输电走廊用地的优点，其承担着高功率和重负荷，因此T型输电线路引起了电力人员的广泛关注[1-2]。一旦线路发生故障，就带来大面积的停电后果，因此，迫切需要研发出新的具有高精度、高速度的测距方法[3-4]。

T型输电线路测距包括故障分支的判别和故障点测距两部分。文献[5]利用参数计算的方法进行T型故障测距,该法比较复杂，而且对信号采集提出了更高的要求。近年来，行波理论应用于T型输电线路故障测距中，更有效地进行故障测距。文献[6]提出利用三个测量端数据进行故障分支判别，但未考虑实际测距误差对测距分支判别带来的影响。文献[7]提出利用3个测量端数据进行故障分支判别，而且考虑了实际误差会带来的分支判别死区，但判别死区会影响故障分支判别。

针对上述问题，笔者提出一种充分利用三端电压电流数据，通过小波变换模极大值[8-11]提取测量点数据信息，进行故障分支判别和测距，并在故障分支判别死区内，提出基于小波能量谱[12-15]进行分支判别的新方法。此方法无需考虑波的折射和反射对行波造成的影响，仅利用第1个小波波头即可进行准确的故障分支判别和测距，在O点附近区域也能准确地分支判别，解决了故障分支判别死区难题。仿真结果表明，对T型线路可以进行精确的故障分支判别和测距。

1 算法介绍及基本理论

1.1 小波变换

小波变换具有良好的时域局部化性能，能在任一小的时间段内给出行波信号在该时刻的频率信息，从而可以快速抓住行波波头，小波还具有抑制噪声的作用。在连续小波变换中，如果只对尺度参数进行离散化，而平移参数保持连续变换，即a=2m,m∈Z,τ∈R,得到二进小波。二进小波变换是一种超完备的、冗余的表达，可用于故障检测和识别。二进小波变换形式为

Wf(2m,τ)=[f(t),Ψ2m,τ(t)]=

(1)

其中:f(t)为原函数；Ψ(τ)为二进小波；Ψ*(τ)为Ψ(τ)的共轭；Wf(2m,τ)为二进小波变换。

设WSf(t)(s=2j)为函数f(t)的二进小波变换，在尺度s下，在t0的某一邻域，对一切t有|WSf(t)|≤|WSf(t0)|,称t0为小波变换的模极大值点，WSf(t)为小波变换的模极大值。

信号奇异点中含有信号最重要的信息，模极大值能刻画出故障行波信号的奇异点和奇异性，小波变换模极大值点和信号突变点相对应，小波变换模极大值极性表示突变点变化方向，大小表示突变点的变化强度，可进行故障检测。分析结果表明，由三次中心B样条函数的一阶导数确定的小波函数(称为三次中心B样条小波函数)是理想的实现信号奇异性检测的小波函数，具有对称性和线性相位优点，在同阶多项式样点函数中具有最小支集。使用db4小波模极大值和三次B样条小波变换模极大值对比如图1所示。可见，三次B样条小波变换模极大值能更清晰准确地提取故障信息，笔者用三次B样条小波函数分析和提取行波信号中的故障信息。

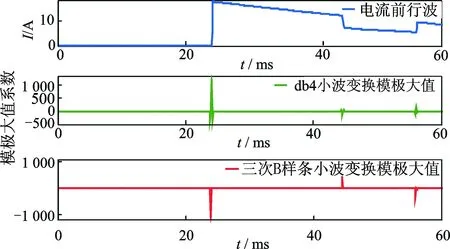
图1 模极大值对比图Fig.1 Modulus maximum contrast diagram

1.2 模分量小波能量谱算法

根据小波能量谱理论，当小波基函数是一组正交基函数时，小波变换具有能量守恒的性质

(2)

其中:Wf(j,k)为信号f的第j层小波变换。

可定义单一尺度下的小波能量为该尺度下重构信号的平方和

(3)

其中：Cj(k)为小波系数；Ej为在尺度j下的重构信号能量；E为信号的总能量。

由此可见，信号的总能量等于小波分解后各尺度下重构信号的能量总和，即小波变换将原始信号分解到不同的频带，每频带内重构信号的能量反应了原始信号在该频带内的能量。因此，通过每个频带内重构信号的小波能量谱来反映原始信号中的能量分布是可靠的。输电线路发生故障后，暂态系统中存在大量的高频信号。实际系统中，高频分量也能够更好地反应故障特征。根据小波能量谱理论对细节系数进行处理，计算其细节能量，并由此来标定暂态信号在定频带所携带的能量，从而得到各个模分量的高频能量如式(4)所示，笔者利用信号模分量的高频分量来代替小波重构信号的能量

(4)

其中:dj(k)为尺度为j时信号小波分解的细节系数。

1.3 波的能量守恒判别

如图2所示，波阻抗为z1和z2的两条输电线路，行波u1q，i1q沿z1向A点传播，其前行功率为

(5)

其中：p1q,u1q,i1q,z1为线路z1的前行功率、行波电压、行波电流和波阻抗。

图2 波的折射和反射Fig.2 Refraction and reflection of waves

当波到达节点A时，能量继续传播，在z2上产生折射波u2q和i2q,相对应的功率为

(6)

其中：p2q,u2q,i2q,z2分别为线路z2的前行功率、行波电压、行波电流和波阻抗。

若z1≠z2, 则必然p1q>p2q,多余的能量(p1q-p2q)必须通过反射波u1f，i1f返回给电源，以使A点处功率平衡，即

p1q-p1f=p2q

(7)

其中：p1f为反射波的功率。

如图3所示的T型输电线路，当MO段发生故障时，沿MO线路的电压行波和电流行波在O前一刻分别设为umq，imq，在O点经过折射后，沿ON和OP线路的行波分别为unq，inq和upq，ipq，在O点反射波为ufq和ifq，它们的功率分别为

(8)

其中：pmq,pnq,ppq分别为线路MO，NO和PO行波的前行功率；pmf为线路MO反射行波功率；umq,unq,upq分别为各支路的行波电压；umf为线路MO反射行波电压；imq,inq,ipq分别为各支路的行波电流；imf为线路MO反射行波电流；zm,zn,zq分别为各支路的波阻抗。

图3 T型线路示意图Fig.3 Schematic diagram of T type circuit

功率平衡公式为

pmq=pnq+pqp+pmf

(9)

由式(9)知：pmq>pnq，pmq>ppq。

当架空导线上不存在电晕时，只考虑导线的电阻和对地电导的耗能作用，波幅的衰减程度很小，当行波到达各测量点时，各点对应的功率下

(10)

PM=PN+PP+PMF+PS

(11)

其中：PM,PN,PP分别为在测量点M，N和P处的行波功率；PMF,PS分别为反射行波在M点的功率和整个线路的损耗功率；UM,UN,UP分别为在测量点处的行波电压；IM,IN,IP分别为在测量点处的行波电流。

由于行波在沿线路传输时，行波的衰减程度很小，行波能量的衰减值远小于行波在O点折射时的损失，在分析行波能量折射和反射变换时，可以忽略波沿线路能量的损失。由式(11)可知，行波在经过O点后，有PM>PN,PM>PP。反之，若发现PM>PN,PM>PP，也可以断定故障发生在OM上。

2 T型线路故障分支判别和测距

图3所示的线路包括MO，NO和PO三条线路，F为故障点。线路长度分别为LMF1，LNF1和LPF1。以MO段线路单相接地故障为例说明T型线路故障分支判别方法，当F点发生故障时，在M，N，P三端放置带有GPS统一时标的行波故障测距装置，可测得故障后到达三端的第1个电流行波波头的时刻，测距方案如图4所示。T型输电线路故障测距包括故障分支判别和故障测距以及O区的故障判别和测距，分别介绍如下。

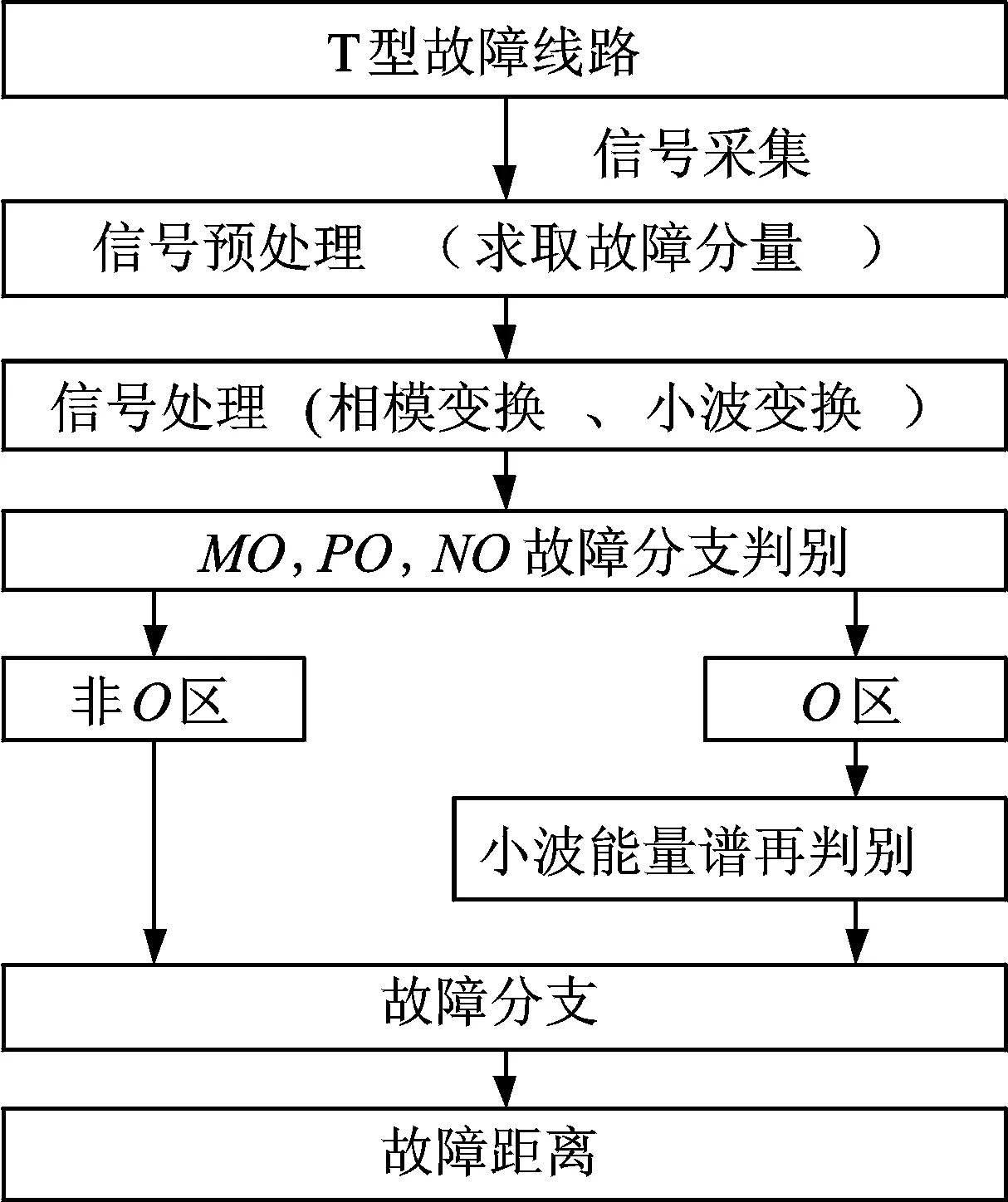
图4 测距方案Fig.4 Location scheme

2.1 T型线路上的故障分支判别

当MO线路发生故障时，克拉克变换解耦合后，由原来的A，B，C三相变成0模和α，β线模分量。笔者选择α线模分量进行小波变换，第1个小波模极大值点对应的时刻即为第1个行波波头到达测量点的时刻。三端测得电流行波波头到达的时刻分别为tM，tN和tP，α线模分量波速为v,利用双端故障测距法测得故障点的距离为

(12)

(13)

其中：LMF1,LNF1,LPF1分别为双端测距法一次测距测得的故障距离；LMN,LNM,LMP分别为线路MN，NM和MP的长度；tM,tN,tP分别为第1个行波波头到达各测距点的时间；LMF2,LNF2,LPF2分别为双端测距法二次测距测得的故障距离；v为线模分量行波波速。

2.2 O区的故障分支判别

当故障发生在半径ε以内时，出现判别盲区，在O区内使用小波变换能量谱算法能够解决此问题。行波在遇到线路结构发生变化的地方发生反射或折射，对于折射而言，功率行波的大小也会发生变化。经过小波能量谱变换后，功率行波的能量与小波能量一一对应，可以通过线路中的M,N和P处小波能量谱中的大小来判断故障分支的位置。如故障发生在M点，由前面分析可知pM>pN，pM>pP。从小波变换能量谱角度分析，M点对应的小波能量大于N点和P点的小波能量，即EM>EN，EM>EP。判断出故障发生在MO段线路,因此解决了因实际测量因素误差导致的测量死区问题。

O区故障分支判别步骤如下：

2) 如果由测量点M,N和P处线模分量的电压和电流计算出线模分量的功率，则对线模分量的功率进行小波能量谱变换；

3) 如果发现此测量点的小波能量谱对应的值明显高于其他两个测量端，则断定此测量点所在的线路即为故障线路分支。

2.3 故障测距

三端测距法可以消除波速不稳定对测距带来的影响，当判断出故障发生在MO断后，根据三点测距法可得

(14)

其中：LMF为测得测量点M到故障点的距离。

3 仿真算例

3.1 仿真算例1

为了验证笔者提出的方法，利用ATP/EMTP电磁暂态仿真软件搭建一个如图3所示的仿真模型。电压等级为220 kV，线路结构参数为：R1=1.8×10-5Ω/m,L1=9×10-4mH/m,C1=1.29×10-5μF/m,R0=1.896×10-4Ω/m,L0=3.43×10-3mH/m,C0=8.3×10-6μF/m, 短路接地阻抗为R=10 Ω。MO段分支线路长为100 km,NO段分支线路长为50 km,PO段分支线路长为80 km,故障时间为0.03～0.05 s,ε取500 m。

在MO段线路70 km处，t=0.03 s时刻发生单相接地故障，分别在M，N，P测量端测量电流故障分量，经过相模变换，得出电流线模电流行波波形如图5所示。小波变换模极大值算法提取出故障发生的时刻，M点对应的小波变换模极大值图如图6所示，图6中纵坐标表示模极大值系数，无量纲单位。计算出M点第1个行波波头到达的时刻为tM=3.023 9 s,N点和P点同理可计算出到达时刻为tN=3.027 4 s和tP=3.037 6 s，线模行波波速为v=2.935×108m/s。由一次测距可以测得LMF1=69.864 km,LNF1=80.136 km,LPF1=110.105 km,LMF2=69.895 km,LNF2=49.885 km,LPF2=80.115 km,|LMF1-LMF2|<1km,|LNF1-LNF2|>1km,|LPF1-LPF2|>1km。由此可判断MO段线路故障，由三端测距法得LMF=69.873 km, 误差为127 m。

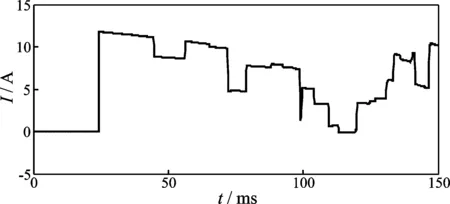
图5 M点电流前行波Fig.5 M point current front traveling wave

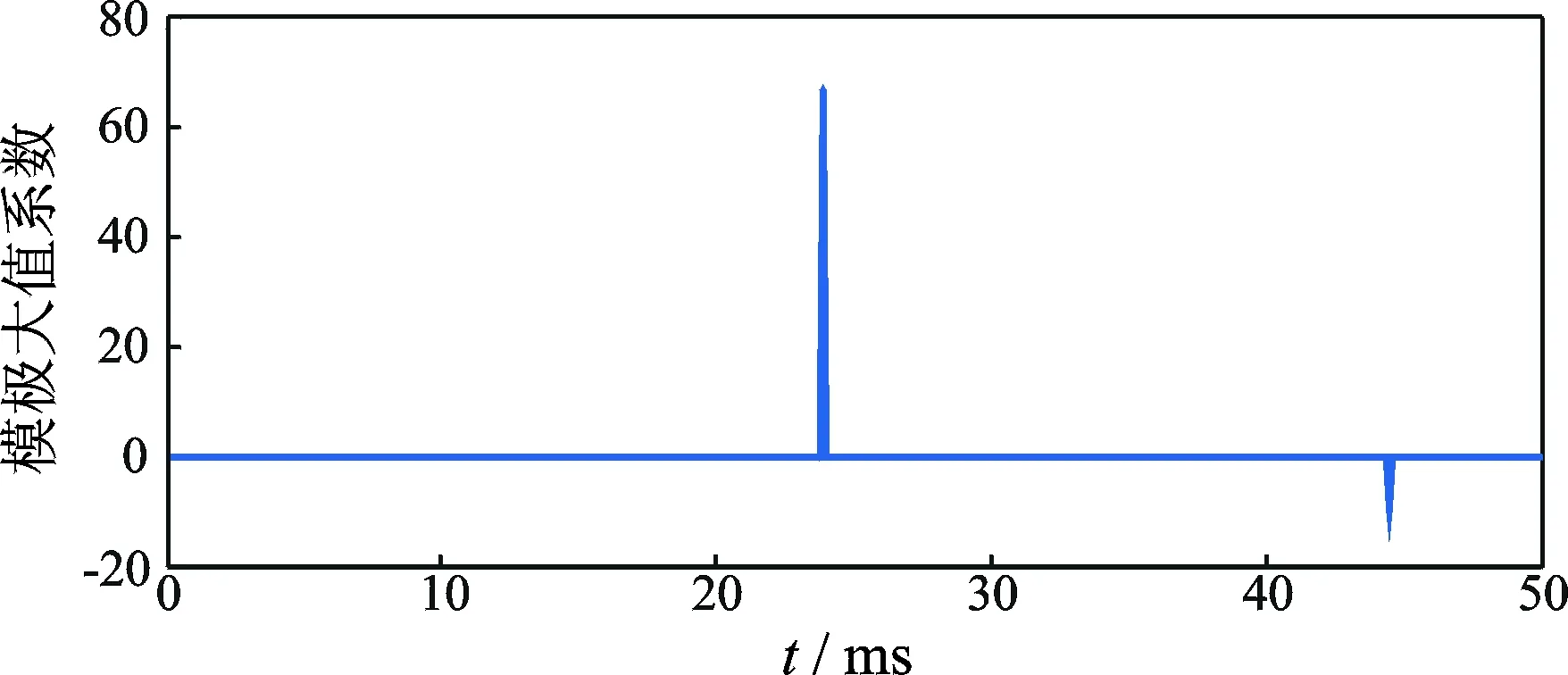
图6 M点小波变换模极大值Fig.6 M point wavelet transform modulus Maxim

3.2 仿真算例2

在MO段线路70 km处，其余同算例1。在测距时分别使用单端测距法、双端测距法和三端测距法进行对比，测距数据见表1。

表1列出了不同故障状态下的非O区故障测距结果，AG，AB，ABG和ABC分别表示A相单相短路、AB两相短路、AB两相接地短路和ABC三相短路故障。由表1可以看出，在不同故障类型和不同故障距离下，都能准确地判断出故障分支，测距相对误差不超过0.19%。

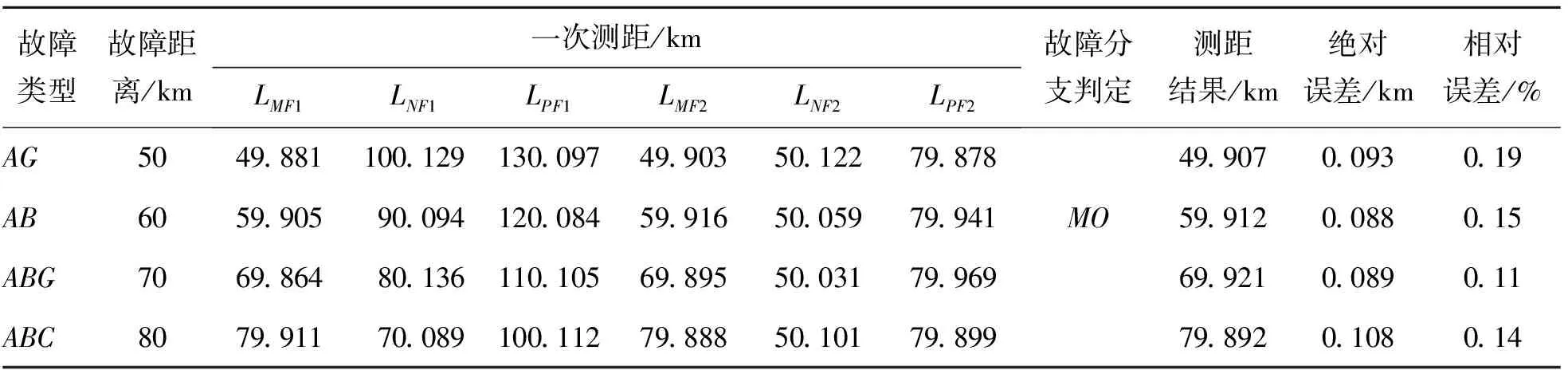
表1 MO段线路故障仿真结果

3.3 仿真算例3

在MO段线路99.7km处，t=0.03 s时刻系统发生单相接地短路故障，测得tM=3.034 2 s,tN=3.017 2 s,tP=3.027 5 s,v=2.935×108m/s。由一次测距可以测得,LNF1=50.247km,LPF1=80.186km,LMF2=99.832km,LNF2=49.875km,LPF2=80.125 km,|LMF1-LMF2|<1 km, |LNF1-LNF2|<1 km,|LPF1-LPF2|<1 km。可见此故障区域在测量死区内，利用小波能量谱法进行判断。M点的功率前行波如图7所示，各测量点对应的功率行波模能量谱如图8所示，图中纵坐标表示小波能量谱幅值，无量纲单位。可以看出M点对应的小波能量谱大于N点和P点，由此判断出故障发生在MO段。由三端测距法测得故障距离为LMF=99.753 km，误差为53 m。

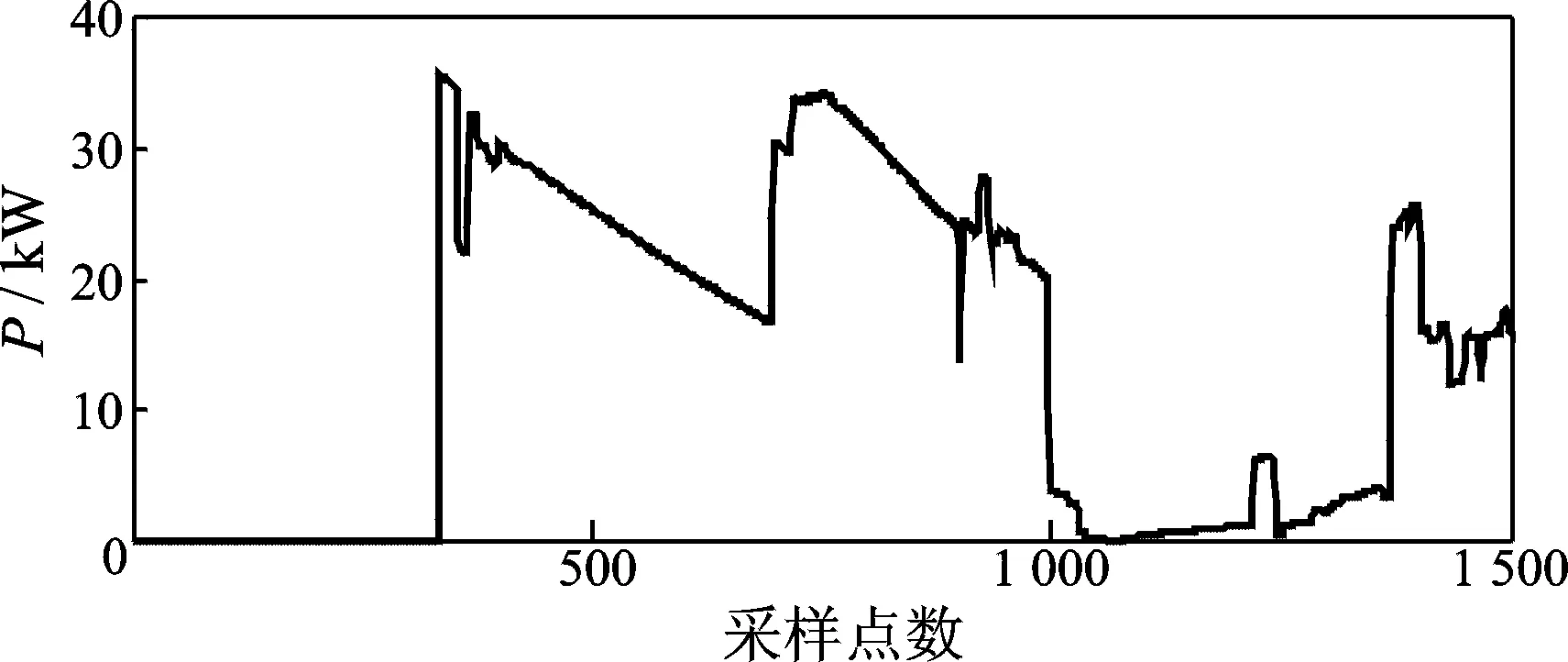
图7 M点功率前行波Fig.7 M point power front traveling wave

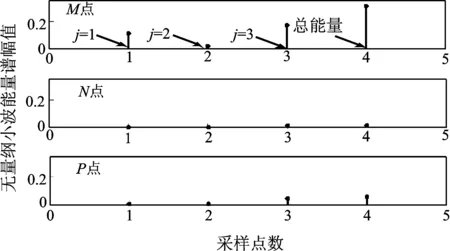
图8 各点对应的小波能量谱变Fig.8 The wavelet energy spectrum transformation corresponding to each point

表2列出了单端测距法、双端测距法和三端测距法的测距比较，由于三端测距法中消除了波速，减小了测距误差，三端测距法的相对误差不超过0.15%。由表2可以看出，在T型输电线路故障测距中，三端测距法的测量精度高于单端测距法和双端测距法。

表3列出了采用小波能量谱算法的O区故障测距结果，仿真MO线路在99.7km处发生故障，各测量点第1个小波波头到达的时刻为tM=0.000 341 s,tN=0.000 172 s,tP=0.000 275 s。对功率行波进行小波变换，计算0～0.000 400s内的小波变换的细节能量谱。由表3可以看出，M点对应的小波能量大于N点和P点，而且测距相对误差不超过0.098%。

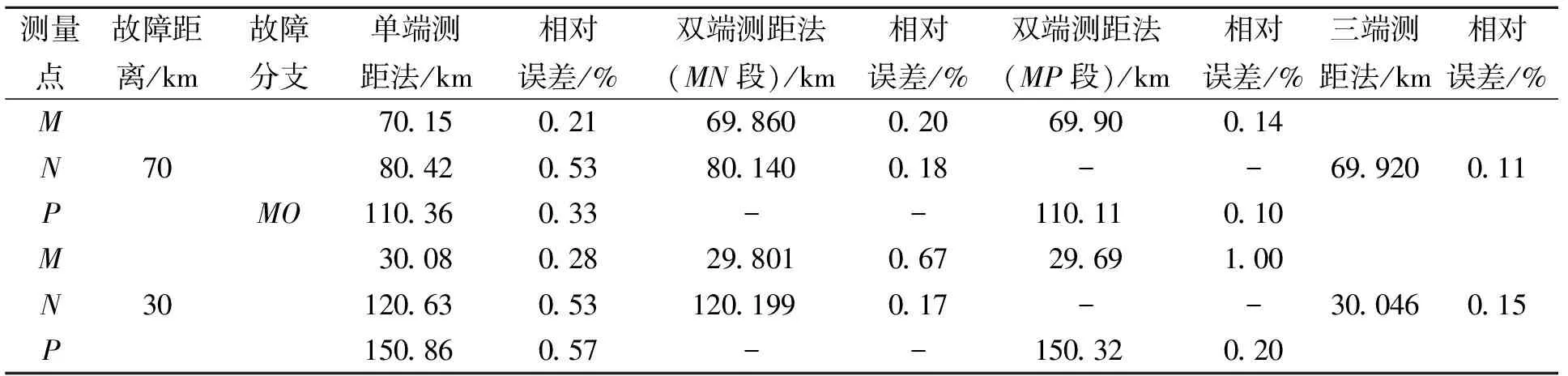
表2 测距法对比

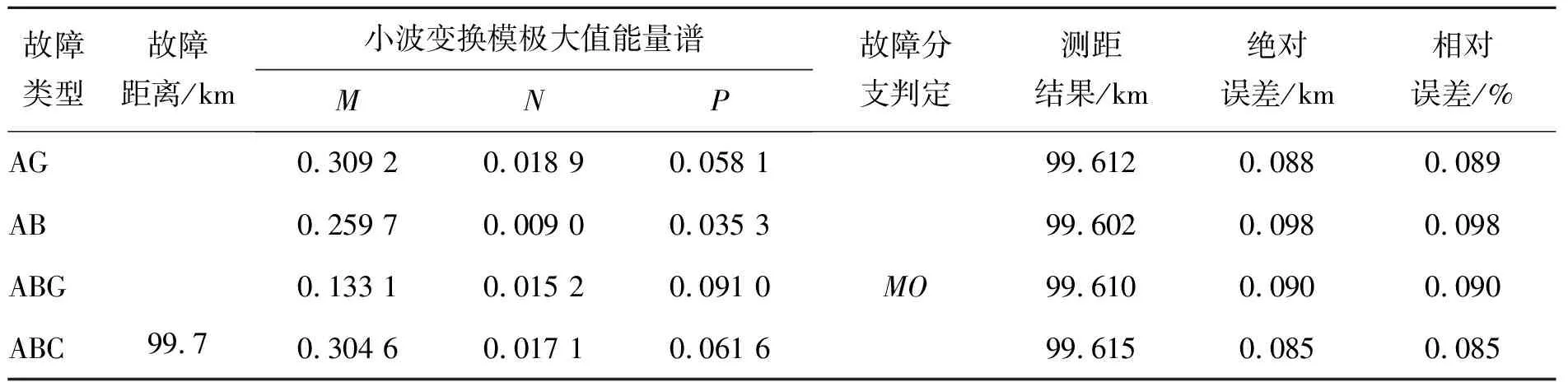
表3 O区线路故障仿真结果

4 结束语

提出了一种T型输电线路故障测距新方法，在考虑实际测距误差的情况下完成了故障分支的判别和测距，并解决了O区的故障分支判别和测距问题。与现有算法相比，所提出的故障测距法充分利用三端电流的测量数据，利用三次B样条小波变换模极大值提取故障信息，有效地消除了波速不稳定对测距造成的影响，提高了测距精度。在O区使用的小波能量谱算法进行故障判支，在一定程度上解决了T型输电线路测量死区的问题，将测距误差降低到0.19%。ATP/EMTP仿真软件仿真结果表明，提出的新算法能满足实际工程应用中的需求，具有一定的实用意义。

参 考 文 献

[1] 王宾, 陆元园. 利用多时刻信息的T接线路单相接地故障单端测距法[J]. 中国电机工程学报, 2016, 36(10): 2611-2618.

Wang Bin, Lu Yuanyuan. Single terminal fault location to single-line-to-ground fault in T transmission line based on sequenced time session data[J]. Proceedings of the CSEE, 2016, 36(10): 2611-2618. (in Chinese)

[2] 韩铭雪, 胡希同, 梁凤强, 等. T型输电线路组合行波测距方法[J]. 电测与仪表, 2016, 53(2): 67-72.

Han Mingxue, Hu Xitong, Liang Fengqiang, et al. Combined traveling wave location method for T transmission line[J]. Electrical Measurement & Instrumentation, 2016, 53(2): 67-72. (in Chinese)

[3] 王召磊, 刘明光. 基于线性方程组解的 T 型线路行波测距[J]. 电网技术, 2014, 38(4): 1047-1050.

Wang Zhaolei, Liu Mingguang. Traveling wave fault location for T transmission line based on solutions of linear equations[J]. Power System Technology, 2014, 38(4): 1047-1050. (in Chinese)

[4] Qin Qiu, Wu N E. A multiple model filtering approach to transmission line fault diagnosis[J]. Control Engineering Practice, 2016, 52: 93-102.

[5] 施世鸿, 何奔腾, 张武军. T型高压输电线路故障测距[J]. 中国电机工程学报, 2011, 31(13): 106-110.

Shi Shihong, He Benteng, Zhang Wujun. Fault location for HV three-terminal transmission lines[J]. Proceedings of the CSEE, 2011, 31(13): 106-110. (in Chinese)

[6] 周鑫, 吕飞鹏, 吴飞, 等. 基于小波变换的T型线路故障测距新算法[J]. 电力系统保护与控制, 2010, 38(2): 9-11.

Zhou Xin, Lü Feipeng, Wu Fei, et al. A new fault location method for T-connection transmission lines based on wavelet transform[J]. Power System Protection and Control, 2010, 38(2): 9-11. (in Chinese)

[7] 陈旭, 朱永利，高艳丰，等. 基于故障分支快速辨识的T型高压输电线路故障定位新算法[J]. 电力系统自动化,2016, 40(4): 105-107.

Chen Xu, Zhu Yongli, Gao Yanfeng, et al. A new fault location algorithm for high-voltage three-terminal transmission lines based on fault branch fast identification[J]. Automation of Electric Power Systems, 2016, 40(4): 105-107. (in Chinese)

[8] 刘习军，相林杰，张素侠. 基于小波分析的简支梁桥损伤识别[J]. 振动、测试与诊断, 2015, 35(5): 866-873.

Liu Xijun, Xiang Linjie, Zhang Suxia. Damage identification of simply supported beam bridges based on wavelet analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5): 866-873. (in Chinese)

[9] 彭畅，柏林，刘小峰. 基于鲁棒性小波包峭度图的滚动轴承故障诊断[J]. 振动、测试与诊断, 2016, 36(1): 11-16.

Peng Chang, Bo Lin, Liu Xiaofeng. Robust wavelet transform-based kurtogram for the fault diagnostics rolling element bearing[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(1): 11-16. (in Chinese)

[10] 张丹, 隋文涛. 基于子小波布置和系数融合的轴承故障诊断[J]. 振动、测试与诊断, 2016, 36(1): 183-186.

Zhang Dan, Sui Wentao. Fault diagnosis of bearings based on baby wavelet deployment and coefficients integration[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(1): 183-186. (in Chinese)

[11] Choudhury A, Paliwal D. Application of frequency B-spline wavelets for detection of defects in rolling bearings[J].Procedia Engineering, 2016, 144: 289-296.

[12] Mookiah M R K, Acharya U R, Lim C M, et al. Data mining technique for automated diagnosis of glaucoma using higher order spectra and wavelet energy features[J]. Knowledge-Based Systems, 2012, 33: 73-82.

[13] 蒋永华, 李荣强, 焦卫东, 等. 应用EMD和双谱分析的故障特征提取方法[J]. 振动、测试与诊断, 2017, 37(2): 338-343.

Jiang Yonghua, Li Rongqiang, Jiao Weidong, et al. Feature extraction method based on empirical mode decomposition and bispectrum analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(2): 338-343. (in Chinese)

[14] 赵新光, 甘晓晔, 谷泉, 等. 基于小波能量谱系数的风力机疲劳裂纹特征[J]. 振动、测试与诊断, 2014, 34(1): 147-152.

Zhao Xinguang, Gan Xiaoye, Gu Quan, et al. Crack fault feature of wind turbine blade based on wavelet energy spectrum coefficient[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 147-152. (in Chinese)

[15] 李晓斌, 赵东阳, 钟光强, 等. 基于小波能量谱的输电线路雷击故障识别方法研究[J]. 电测与仪表, 2014, 51(12): 35-39.

Li Xiaobin, Zhao Dongyang, Zhong Guangqiang, et al. Identification method of lightning fault for transmission lines based on wavelet energy spectrum[J]. Electrical Measurement & Instrumentation, 2014, 51(12): 35-39. (in Chinese)