拼接模具过缝区域切削力建模与表面质量*

刘献礼， 高海宁， 岳彩旭， 姜 男

(哈尔滨理工大学机械动力工程学院 哈尔滨，150080)

1 问题的引出

汽车覆盖件模具有结构尺寸大、形状复杂及尺寸精度要求高的特点。材料Cr12MoV和7CrSiMnMoV是汽车模具常采用的材料，其淬火后硬度可达HRC50～HRC65，属于典型高强度和高硬度材料[1-2]。汽车模具制造企业常采用硬态铣削技术来提高生产效率，并引入了高速切削工艺。上述两种工艺有机结合显著提高了加工效率，并改善了加工条件。将镶式淬硬钢模件拼接后整体铣削加工来提高覆盖件模具的加工效率，这是一种常用方法。拼接模具的模件间存在的硬度差一般为ΔHRC5～ΔHRC10，有的甚至高达ΔHRC15，并且拼接镶块件拼接缝最大可达2 mm。带镶块不同硬度模件拼接处细节如图1所示。在过拼接缝区域时铣削存在切入切出冲击以及硬度差引起的载荷突变，对刀具造成明显的振动冲击，使得刀具极易产生早期破损，严重影响刀具的使用寿命，且降低了已加工表面型面精度。

切削力直接影响切削过程中切削系统的振动、铣削稳定性[3-4]、尺寸误差[5]和加工精度[6]。为此，国内外学者对切削过程中切削力建模进行了深入研究。由于球头铣刀的铣削过程及力学机制的复杂性，直到1991年，Yang等[7]从正交切削试验中获得了基本的切削参数，并考虑了由于静态刀具偏转引起的切屑载荷的变化，得到了球头铣刀加工的铣削力模型。Lee等[8]基于球头铣刀几何模型[9]建立了球头刀的瞬时刚性力模型。采用正交切削参数(即剪切应力、剪切和摩擦角)及局部铣削力系数之间的精确转换方法[10]得到了切削力系数。统计和采样时域仿真结果表明，所提方法可以准确预测任何几何形状和切削条件下的切削力。Ko等[11]使用不受切削条件影响的瞬时切削力系数得到三维球头铣削的机械式切削力模型，其中未切屑厚度模型考虑了刀具变形和刀具偏心的影响。Ozturk等[12-13]提出一种确定刀-工接触区域的分析方法，并对切削力系数进行了修正，得到了球头铣削自由曲面的切削力预测模型，预测误差在10%之内，证明了该方法的有效性。Wei等[14]根据刀具轨迹上每齿进给量把等高曲面加工分成小斜平面的组合，基于改进Z-Map模型得到了快速确定刀具切出区域的方法，得到了曲面加工铣削力预测模型，之后又提出一种半解析方法得到刀-工接触区域[15]。Wan等[16]将建立铣削力预测模型分解为刀具侧刃部分和底刃部分，并使用线性回归校准切削力系数对铣削力进行精准预测。Sun 等[17]在刀轴方向的连续变化下通过扫描切削刃轨迹方法得到考虑刀具偏心的未变形切削厚度，对五轴铣削过程瞬时铣削力进行了预测，通过不同实例验证了所提方法的有效性。Yue 等[18]在拐角铣削过程中建立了基于拐角真实轨迹切屑厚度数学模型，获得了准确的铣削力预测模型并进行了试验验证。

图1 汽车覆盖件模具多硬度模件拼接区域图Fig.1 Multi-hardness module splicing area diagram of automobile panel die

何耿煌等[19]对断续加工过程的冲击进行了研究，揭示了刃口对刀片的强化作用机理。Davies等[20]针对断续切削工况，把切削过程建成涉及延迟效应的碰撞模型，并对模型进行了试验验证。基于上述模型，Szalai等[21]针对低径向切深高速铣削工况建立了离散数学模型，并对稳定性边界进行了亚临界分岔分析。由于过拼接缝处存在瞬时冲击力以及同一刀齿切削不同硬度材料，致使传统切削力建模并不适用。为此，笔者在传统刚性切削力模型的基础上，引入单自由度斜碰撞模型，建立了拼接模具过缝区域切削力微元模型，结合切削试验对所提切削力模型进行验证。所建立的切削力预测模型为改善工件表面质量、提高切削效率和延长刀具使用寿命等提供了理论依据。

2 单自由度斜碰撞模型

球头铣刀跨拼接缝切向另一硬度材料时，刀具与工件成一定角度接触，因此可以认为刀-工接触模型为单自由度斜体碰撞模型。

2.1 法向接触力模型

接触碰撞过程可以看作是连续动力学问题，其过程碰撞力可以等效成弹簧阻尼模型来得到[22]。法向接触力的求解公式为

(1)

依据赫兹弹性接触理论，在两种接触体形状较为规则(如圆球或圆柱时)的前提下，接触刚度系数可以由材料的弹性模量、泊松比推导出碰撞模型的接触刚度系数

其中：R1,R2分别为两接触物体在接触点的接触半径；μ1,μ2分别为两物体材料的泊松比；E1,E2分别为两接触物体材料的弹性模量。

运用等效弹簧阻尼方法求解接触碰撞问题的关键是选择合理的接触力模型。文献[23]提出了如下形式的迟滞阻尼模型

D=cδe

(5)

其中：c为迟滞阻尼因子。

c的计算公式为

(6)

将式(5)、式(6)带入到式(7)得

(7)

2.2 切向接触力模型

在接触碰撞的过程中两个接触物体有相对滑动，切向方向会受到摩擦力的作用，斜碰撞中经常出现切向摩擦力。笔者考虑的摩擦力是基于Coulomb摩擦力，其主旨思想为:摩擦力与法向载荷成正比，且与运动方向相反，不依赖于接触面积。得到切向接触力模型

Fs=uFncosθst

(8)

3 拼接处切削力模型

笔者选用文献[8]提出的瞬时刚性力模型来建立拼接缝过程中切削力模型。在模具拼接处铣削加工过程中，刀具要经历由一个拼接模件到拼接缝，最终再到另一个拼接模件的过程，其过程如图2所示。由于拼接缝的存在，刀具在由一个拼接模件切向另一个拼接模件的过程中，要经历二次切入切出，而二次切入过程中将导致碰撞冲击力的引入，故在球头铣削加工模具拼接区域的铣削力模型中需要进行分阶段划分与修正。

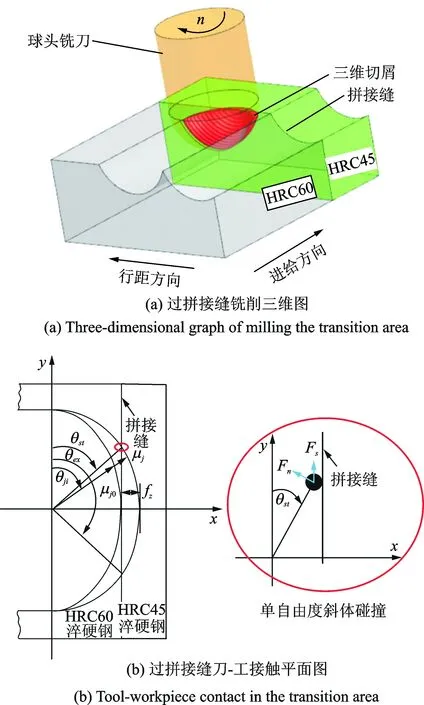
图2 拼接缝切削示意图Fig.2 A schematic diagram of cutting in the transition area

基于瞬时铣削力模型[8]得到过拼接缝处切削微元切向力、径向力和轴向力分别为

(9)

其中：dFi1，dFi2分别为两种不同硬度材料的三向微元力；i=t,r,a。

在图2切削位置时，硬度为HRC60材料的微元切削力为

(10)

瞬时切削厚度tn1计算公式为

(11)

其中：θ为切削刃微元点的位置角；κ为切削刃微元点的轴向位置角；θst，θex分别为切削刃的切入切出角；R为刀具半径；fz为每齿进给量。

具体空间位置关系如图2所示。

(12)

瞬时切削厚度tn1计算公式为

(13)

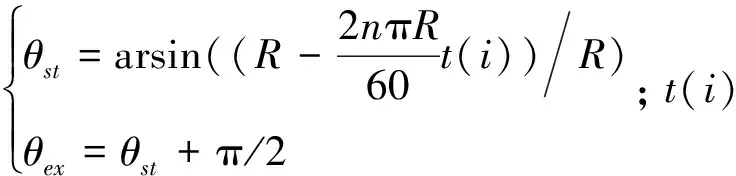
刀具要经历由一个拼接镶块到拼接缝，最终再到另一个拼接镶块的过程，二次切入冲击力为

(14)

作用在切削刃上的总的切削力为

(15)

其中：θup，θdown为轴向积分角。

4 试验与仿真

4.1 工件弹性变形量的获取

在拼接缝处二次切入模型应用斜碰撞模型的前提是刀具-工件发生的是弹性变形。为得到碰撞物体弹性变形量δ，笔者选择霍普金森试验来得到刀-工在动态力学性能情况下的弹性变形量，进而得到过缝处刀具所受的冲击力。霍普金森压杆试验设备如图3所示，试验测试软件为Arcimedes Alt1000，系统瞬态最高采样速率为1 MHz，每通道独立A/D模数转换器，外挂应变调理器完成1/4桥、半桥及全桥状态的应力应变测试和分析，对被测信号实时采集、实时显示、实时存储和实时分析，具备自动测试控制和数据波形分析处理功能。为得到硬度分别为45HRC，60HRC的淬硬钢试样的动态真实应力-应变曲线，试验的几何尺寸长度为5 mm，直径为10 mm。

图3 霍普金森实验设备Fig.3 Hopkinson experimental equipment

4.2 切削试验

本次加工试验，拼接模具材料为Cr12MoV，其硬度分别为45HRC和60HRC。两块硬度不同的工件通过夹具安装在压电式测力仪上，测力仪的型号为Kistler9257B。三向加速度传感器粘贴在工件上，将采集的振动信号经电荷放大器放大后由数据采集箱将电信号转化成数字信号，电荷放大器型号为Kistler5070A，数采箱系统为DH-5922。试验刀具采用日本戴杰公司生产的型号为BNM-200的球头铣刀，刀尖圆弧半径为10 mm，切削刃钝圆半径为20 μm，悬深为130 mm。本研究试验机床为奥地利EMCO公司生产的三轴数控铣床。拼接模具钢的加工现场如图4所示。

图4 淬硬钢拼接件加工现场Fig.4 Machining site of harden steel split workpiece

4.3 试验结果分析

图5 不同硬度不用切削速度下应力-应变曲线Fig.5 Stress-strain curves with different hardness at different cutting speeds

图5为室温条件且不在主轴转速下获得的不同硬度淬硬钢材料的真实应力-应变曲线。图5(a)为硬度60HRC淬硬钢真实应力-应变曲线，图5(b)为硬度45HRC淬硬钢真实应力-应变曲线。两图中每一条曲线的第一阶段为材料弹性变形阶段，即为碰撞模型弹性变形量δ。对比图5(a),(b)中的4条曲线可以得到，在弹性变形阶段,随着主轴转速的增加，相同应力下不同硬度的弹性变形量(真实应变)逐渐增大，此过程真实应力应变呈非线性关系。得到不同转速下不同硬度淬硬钢随时间变化的真实应应变曲线如图6所示。

由刀-工接触关系可知：R1=4.8 mm；R2=∞；工件弹性模量为180 GPa，泊松比为0.3；刀具弹性模量为600 GPa，泊松比为0.2。进而得到刚度系数K=1.51e5，e=1.5。阻尼系数和恢复系数通过试验来获得[24]，经查可得u=0.15。

加工参数为：n=4 kr/min；ap=0.3 mm；fz=0.1 mm；进给方向为高硬度到低硬度下过拼接缝处。试验得到x方向上的切削力及对应的切削振动如图7所示，由图可知，由高硬度材料切向低硬度材时切削力逐渐减小，而切削过缝处的振动变化规律为先增大后减小，最后趋于稳定。造成的原因是存在切削瞬时冲击，证明了引入碰撞冲击思想的正确性。

4.4 切削力预测与试验结果对比分析

图8是在加工参数为：n=4 kr/min；ap=0.3 mm；fz=0.1 mm；进给方向为高硬度到低硬度下拼接缝区域及铣削60HRC淬硬钢得到x，y，z方向上的试验及仿真切削力。

图6 不同转速下工件弹性应变曲线Fig.6 Workpiece elastic strain curves at different speeds

图7 x方向切削力及振动Fig.7 Cutting force and vibration in the x direction

由图8可知：铣削拼接件过程及单硬度材料的三方向上，试验力与仿真力无论是在趋势上还是在幅值上都具有很好的一致性；在x和y两方向上存在明显的切入冲击力；在z方向上切入冲击力并不明显，可以忽略，与所建立的切削力预测模型一致。过缝处x,y两方向上的冲击力随着切削时间的推移而逐渐减小，这是因为随着时间的进行，切削刀具与工件碰撞的接触点所在圆的半径逐渐减小，并且接触点空间位置角随时间逐渐减小。对比过缝前x，y，z三方向上试验力和仿真力可得，最大绝对误差分别为11.11%，10.34%和9.56%。对比过缝中x，y，z三方向上试验力和仿真力可得，切削刃在每一切削周期切屑厚度最大处的误差分别为12.56%，10.25%和10.12%。在拼接缝处x，y方向上冲击力最大误差分别为15.45%和17.26%。造成冲击力仿真误差偏大的原因为：a.假定刀-工碰撞时，只有工件发生弹性形变量，而忽略刀具的弹性形变量；b.利用霍普金森压杆试验获得工件弹性变形量受试验条件影响，存在一定的偏差。以上所有误差均在可接受误差范围内,证明了所建切削力预测模型的正确性。

5 过缝处表面质量

图9为不同铣削方向(低硬度45HRC到高硬度60HRC或高硬度到低硬度)在超景深倍数为200倍下垂直拼接缝铣削得到的已加工表面质量图。图10为不同铣削方向在白光干涉仪下得到的已加工表面质量微观图。

由图9(a)和图10(a)可知，低硬度切向高硬度时过缝处两侧发生了过切、破损和崩碎现象，并且切入端的崩碎区域的宽度普遍要大于切出端。造成上述现象的原因为：a.过缝处切削力逐渐增大；b.刀-工件碰撞时的弹性变形量增大，进而瞬时冲击力增大。由图9(b)和图10(b)可知，过拼接缝处存在硬度60HRC工件材料没有成功被剪切，而挤压到拼接缝隙中，产生毛刺，影响已加工表面质量。同时存在着工件破损现象，但相对于低硬度到高硬度破损程度要低。

由上述分析可知，无论是低硬度切向高硬度还是高硬度切向低硬度材料，过缝处材料都会出现破损现象，但后者破损程度小。低硬度切向高硬度易出现过切现象，高硬度切向低硬度易出现欠切现象。工件欠切可以通过后续工序进行修正，进而得到合格产品；而过切直接会造成产品报废。因此，在过拼接缝方向上应选择高硬度材料切向低硬度材料。使用Talysurf CCI白光干涉表面轮廓仪测量平面工件在拼接缝处的表面质量，得到纳米级精度下表面粗糙度(见表1)以及两工件之间缝隙的高度差(见图11)。为了准确表达拼接缝区域的表面粗糙度，选用垂直和平行于拼接缝两个方向进行测量。

图8 x，y，z三方向试验力与仿真力对比Fig.8 Comparison of experimental force and simulation force in three directions of x, y and z

图9 不同铣削方向下已加工表面质量Fig.9 Machined surface quality in different milling directions

图10 不同铣削方向下已加工表面质量微观图Fig.10 Micrograph of machined surface quality under different milling direction

由表1可知，铣刀过缝方向为低硬度到高硬度时，45HRC工件在缝隙处表面粗糙度无论是平行方向还是垂直方向都高于60HRC工件的表面粗糙度。铣刀过缝方向为高硬度到低硬度时，两硬度工件在缝隙处的表面粗糙度值相差不大，且都小于低硬度切向高硬度方向的表面粗糙度值。

在已加工表面垂直于拼接缝测量两工件的高度差，可以揭示由于过拼接缝处冲击引起的表面质量。不同铣削过缝方向下两工件之间的高度差如图11所示。

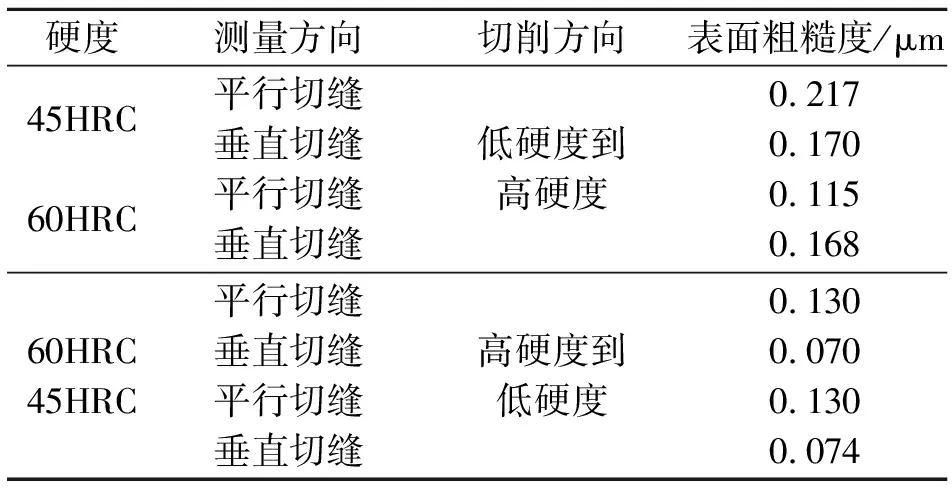
表1 过缝角度对切缝附近的表面粗糙度的影响

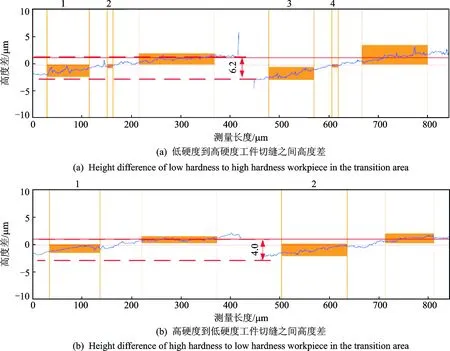
图11 工件切缝之间的高度差Fig.11 The height difference of the workpiece in the transition area

对比图11(a)和(b)可知：高硬度到低硬度工件切缝之间高度差低于低硬度到高硬度工件切缝之间高度差，这是因为当铣刀由高硬度铣向低硬度时，切削力和刀-工件的瞬时冲击力减小，刀具发生弯曲变形和切削振动减小，进而使得拼接件高度差减小。工件表面完整性与零件的使用性能存在直接关系。由已加工表面质量、表面粗粗度及拼接件之间的高度差分析结果可得，铣削不同硬度拼接模具铣削方向宜从高硬度材料切向低硬度材料，所得结论与文献[25]相同。

6 结 论

1) 建立了过拼接缝处铣削力预测模型。对比过缝前x，y，z三方向上试验力和仿真力可得，绝对误差分别为11.11%，10.34%和9.56%。

2) 在拼接缝处x，y方向上冲击力误差分别为15.45%和17.26%。造成冲击力仿真误差偏大的原因为假定刀-工碰撞时，只有工件发生弹性形变量，而忽略刀具的弹性形变量；利用霍普金森压杆试验获得的工件弹性变形量受试验条件影响，结果存在一定偏差。

3) 在x，y两方向上存在明显的切入冲击力，在z方向上切入冲击力并不明显；且过拼接缝铣削时，从高硬度到低硬度为推荐切削方向。

参 考 文 献

[1] Altan T, Lilly B, Yen Y C, et al. Manufacturing of dies and molds[J]. CIRP Annals-Manufacturing Technology, 2001, 50(2):404-422.

[2] 姜彦翠, 刘献礼,丁云鹏，等.汽车大型覆盖件淬硬钢模具切削加工技术[J]. 哈尔滨理工大学学报,2013,18(1)：7-13.

Jiang Yancui, Liu Xianli, Ding Yunpeng, et al. Machining technology of hardened steel molds of automobile large covering[J]. Journal of Harbin University of Science and Technology, 2013,18(1)：7-13.(in Chinese)

[3] Liu Xianli, Li Rongyi, Wu Shi, et al. A prediction method of milling chatter stability for complex surface mold[J]. The International Journal of Advanced Manufacturing Technology, 2017, 89(9-12): 2637-2648.

[4] Yue Caixu, Liu Xianli, Liang S Y. A model for predicting chatter stability considering contact characteristic between milling cutter and workpiece[J]. The International Journal of Advanced Manufacturing Technology, 2017, 88(5-8): 2345-2354.

[5] Oliaei S N B, Karpat Y. Influence of tool wear on machining forces and tool deflections during micro milling[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(9-12): 1963-1980.

[6] Wan Min, Zhang Weihong, Wang Zhenpei. Strategies for error prediction and error control in peripheral milling of thin-walled workpiece[J]. International Journal of Machine Tools and Manufacture, 2008, 48(12): 1366-1374.

[7] Yang Minyang, Park H. The prediction of cutting force in ball-end milling[J]. International Journal of Machine Tools and Manufacture, 1991, 31(1): 45-54.

[8] Lee P, Altintas Y. Prediction of ball-end milling forces from orthogonal cutting data[J]. International Journal of Machine Tools and Manufacture, 1996,36(9):1059-1072.

[9] Yucesan G. Mechanics of ball end milling process[J]. ASME Manufacturing Science and Engineering, 1993, 64: 543.

[10] Altinta Y, Armarego E J A. Prediction of milling force coefficients from orthogonal cutting data[J]. Journal of Manufacturing Science and Engineering, 1996, 118(2): 216-224.

[11] Ko J H, Cho D W. 3D ball-end milling force model using instantaneous cutting force coefficients [J]. Journal of Manufacturing Science and Engineering, 2005, 127(1): 1-12.

[12] Ozturk B, Lazoglu I. Machining of free-form surfaces. part I: analytical chip load[J]. International Journal of Machine Tools and Manufacture, 2006, 46(7): 728-735.

[13] Ozturk B, Lazoglu I, Erdim H. Machining of free-form surfaces. part II: calibration and forces[J]. International Journal of Machine Tools and Manufacture, 2006, 46(7): 736-746.

[14] Wei Zhaocheng, Wang Minjie. Cutting force prediction in ball end milling of sculptured surface with Z-level contouring tool path[J]. International Journal of Machine Tools and Manufacture, 2011, 51(5): 428-432.

[15] 魏兆成,王敏杰,王学文, 等.球头铣刀曲面多轴加工的刀具接触区半解析建模[J].机械工程学报, 2017,53(1):198-205.

Wei Zhaocheng, Wang Minjie, Wang Xuewen, et al. A semi-analytical cutter workpiece engagement model for ball end milling of sculptured surface[J]. Journal of Mechanical Engineering, 2017,53(1):198-205.(in Chinese)

[16] Wan Min, Lu Mingsheng, Zhang Weihong, et al. A new ternary-mechanism model for the prediction of cutting forces in flat end milling[J]. International Journal of Machine Tools and Manufacture, 2012, 57: 34-45.

[17] Sun Yunwen, Guo Qiang. Numerical simulation and prediction of cutting forcer in five-axis milling processes with cutter run-out[J]. International Journal of Machine Tools and Manufacture, 2011, 51(10/11):806-815.

[18] Yue Caixu, Liu Xianli, Steven Y,et al. A model for predicting chatter stability considering contact characteristic between milling cutter and workpiece[J]. The International Journal of Advanced Manufacturing Technology,2017,88(5):2345-2354.

[19] 何耿煌, 李凌祥, 邹伶俐, 等. 亚微观倒棱切削刃对硬质合金刀片切削性能的影响特性研究[J]. 金刚石与磨料磨具工程, 2017, 37(3): 46-54.

He Genghuang, Li Lingxiang, Zou Lingli, et al. Influencing characteristic of submicroscopic chamfering cutting edge on the cutting property of cemented carbide insert[J]. Diamond & Abrasives Engineering,2017,37(3):46-54.(in Chinese)

[20] Davies M A, Pratt J R, Dutterer B, et al. Stability prediction for low radial immersion milling[J]. Journal of Manufacturing Science & Engineering, 2002, 124(2):217.

[21] Szalai R, Stépán G, Hogan S J. Global dynamics of low immersion high-speed milling[J]. Chaos, 2004, 14(4):1069-1077.

[22] 刘才山,陈滨. 多柔体系统碰撞动力学研究综述[J].力学进展,2000(1):7-14.

Liu Caishan, Chen Bin. A global review for the impact dynamic research of flexible multibody systems[J].

Advances In Mechanics, 2000(1):7-14.(in Chinese)

[23] Lankarani H M, Nikravesh P E. Continuous contact force models for impact analysis in multibody systems[J]. Nonlinear Dynamics, 1994, 5(2): 193-207.

[24] Ahn K Y, Ryu B J. A modeling of impact dynamics and its application to impact force prediction[J]. Journal of Mechanical Science and Technology, 2005, 19: 422-428.

[25] 岳彩旭,高海宁,张海涛,等.汽车覆盖件拼接模具硬态铣削过程的动态特性[J].振动、测试与诊断,2017,37(4):822-829.

Yue Caixu, Gao Haining, Zhang Haitao, et al. Research on dynamic characteristics of hard milling process of splicing dies for automobile cover panel[J].Journal of Vibration,Measurement & Diagnosis,2017, 37(4):822-829. (in Chinese)