基于PH乘子算法优化的Lamb波成像研究*

李培江， 朱晓锦， 尤 婷， 张合生， 方昱斌

(1.上海大学机电工程与自动化学院 上海，200072) (2.衢州职业技术学院信息工程学院 衢州，324000) (3.衢州学院电气与信息工程学院 衢州，324000)

引 言

超声检测具有检测能力强、检测范围广、检测速度快及无污染等优点，在结构健康监测中得到十分广泛的应用。超声波在介质表面传播时会产生表面波，在薄板中传播就产生了Lamb波，Lamb波能够同时检测构件的整个界面，实现长距离检测，可高效地实现对薄板、管道的扫描[1-2]。由于Lamb波传播机理的复杂性，远距离的传播过程中往往叠加其他模态和边界反射信号，这给损伤的识别与定位造成许多困难[3]。

Lamb波是频散的板波，与传统的点对点应用超声体波(纵波和横波)的检测方法相比，Lamb波检测具有一处激励大面积传播的优势，检测快捷而且高效。为了进一步对损伤位置进行确定，需要探讨一些将损伤情况可视化，可以为定量确定损伤的位置、识别损伤的程度提供一种快速直观的成像算法。

近些年，许多学者在成像算法上进行了研究。杜云朋等[4]以导波回波信号为基础，提出了一种基于改进粒子群算法的最小二乘支持向量机的缺陷二维轮廓重构方法。Wilcox利用电磁超声阵列传感器，激发单一的S0模态Lamb，相位延迟叠加算法进行成像[5-6]。Yu等[7-8]利用相控阵的波束成形特性，通过添加相位延迟的信号接收的数组元素和增加延迟的信号实现了缺陷成像。Yu等[9]利用虚拟相控的方式实现了S0模态的Lamb波整板成像。张海燕等[10]基于时间反转理论提出了一种板材的成像检测。Hettler等[11]通过利用不同的激励幅度电平所获得的导波信号，以取代完整基准信号，改进了传统的成像方法。刘彬等[12]在椭圆轨迹法确定各通道损伤因子的有效影响区域的基础上，对复合材料T型接头实现了概率成像。孙汝杰等[13]将核密度估计方法用于结构的损伤成像识别中，提高了识别效率。

笔者将包络幅值的方法应用到导波检测中，在保证所需要方向信号不变的情况下，实现了铝板中缺陷的定位，并且将乘子法引入到导波成像算法中实现像素点参数的优化，以进一步提高成像的质量。实验结果表明了该成像优化方法的可行性。

1 导波检测传播分析

图1为检测模型示意图。图中圆形区域表示压电传感器，分别作为驱动器和传感器；不规则区域为损伤。选择其中一个压电片作为驱动器，然后施加一个激励信号，通过驱动器就可以在结构中引入弹性诊断波。虽然驱动器产生的弹性波在材料中会有多种不同的传播路径，但是损伤定位只需要关心那些经过损伤到达传感器的信号即可。图1中实线所示的路径就是没有经过损伤的信号，其中的波包不含有损伤信息，导波信号会受到缺陷影响发生传播方向、相位与幅值改变；而虚线所示的路径是导波经过损伤反射后到达传感器的信号，是需要关注的信号。对接收的信号做进一步分析，可以确定缺陷位置。判别缺陷位置之前，需要预先提取出无缺陷的健康信号——基准信号[14]，实际接收的信号与基准信号进行相减运算后使得缺陷特征突出。为了提高信噪比，需要对每条信号通道进行多次采样、平均后才能作为基准信号。

图1 导波信号传播路径Fig.1 The paths of guided wave signal propagation

2 包络幅值成像原理

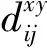
(1)

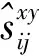
利用包络曲线与发送-接收传感器位置关系可以设定坐标点的像素值

(2)

其中：eijxy为权重系数，反映像素点(x,y)和第i个发送-第j个接受传感器位置相关程度；w(t)为窗函数。

将式(2)改写成式(3)的单积分形式

(3)

由于导波的信号处理主要通过向量的运算来实现，因此将式(3)表示成式(4)的向量形式

(4)

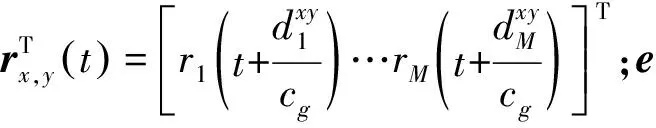
e的选取由式(5)得到

(5)

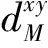
因此，式(4)可以改写为

(6)

其中：eH为e的Hermitian矩阵形式；Rx,y为时空互相关矩阵。

Rx,y表示为以下形式

(7)

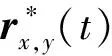
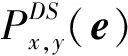
包络幅值响应的方法使用了阵列信号处理方式，其原理是将多个传感器设置在空间不同位置组成传感器阵列，利用这一阵列对空间信号场进行接收和处理，目的是提取阵列所接受信号及其特征信息，同时抑制干扰和噪声[16-17]。导波在若干位置上的输出响应中含有缺陷信号，因此在保证无失真条件下，一方面要实现缺陷的定位，另一方面要使得噪声输出最小，成像干扰最小[18]。

对于时空互相关系数矩阵Rx,y，可以表示成式(8)的特征分解形式

(8)

其中：λi为特征值；vi为Rx,y与相关的单位范数特征向量。

由于Rx,y具有Hermetian对称，所以每个特征值是非负的，而且特征向量彼此正交。假设式(8)中特征值是由大到小依次排列好的，则λ1为最大的特征值，v1为最大值所对应的特征向量。

由于缺陷引起的反射信号x(t)都包含了共同的能量信号，设图1中缺陷位置坐标点为(c,d)，则该位置反射信号可以表示为

rc,d(t)=x(t)s

(9)

其中：s为随x(t)变动的单位范数特征向量。

依照式(8)的关系，对于缺陷位置，令x(t)=λ1，s=v1，非缺陷位置反射能量信号x(t)=0，则缺陷(c,d)处的回波信号由式(10)得到

(10)

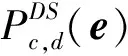
导波检测中，往往因为传感器数量有限且存在干扰，为了减少成像像素点的干扰，一般要求非缺陷位置的像素值要小，而e反映了像素点和发送-接受传感器位置相关程度，体现了像素权重值，包络位置响应的思想是在保证所需要方向的信号不变的情况下，使得对应的点的像素值最小。在噪声(包括干扰)与信号不相关的假设下，成像求解如式(11)所示

(11)

其中：w为权重导向矢量。

因此，为了提高像素质量，像素值的选取实际上是一个基于式(11)的优化问题

minwHRx,yw

(12)

其中：wHe=1；w为满足该式的权重矢量。

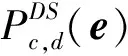
现实生活中，老师和家长对孩子的异性交往非常敏感，责难有余，指导不足。致使异性交往这个最需要老师和家长指导的问题，却成了孩子最怕老师和家长知道的问题。于是，有些孩子得到了偶然的帮助跳出了“爱河”，有些孩子没有得到适当的帮助，虽然不甘沉溺却又身不由己地在“爱河”中淹溺了自己的学业和青春。可以这样说，孩子们面对初恋之情，他们往往不是不想说“不”，而是不会说“不”。有时候，成人一个小小的点拨，就会让他们找到告别“爱河”的路径。

wHRc,dw=λ1|wHe|2

(13)

由式(13)可以看出，w和e内积的限制使得缺陷位置的像素值为最大λ1，从而使像素值限定在一个合适的范围。

3 PH乘子算法的成像优化

求解式(10)的最优问题有很多种方法，笔者提出的PH乘子算法的基本思想是：从原问题的拉格朗日函数出发，加上适当的罚函数，从而将原问题转换为求解一系列无约束优化问题，最后得到最优解，改善成像质量[19]。

因此，针对上述关于导波成像的公式推导，提出优化模型为

(14)

将式(14)转换成拉格朗日函数为

(15)

其中：λ=(λ1,λ2,…λl)为乘子向量。

设(w*,λ*) 为式(14)的卡罗需-库恩-塔克(Karush-Kuhn-Tucker，简称KKT)对，则由最优性条件有

wL(w*,λ*)=0

(16)

当σ>0适当大时，w*为ψ(w,λ*,σ)的极小值点。由于乘子向量λ事先并不知道，则可以考虑以下的增广目标函数

(17)

其求解算法过程执行如下：

1) 给定初始值w0∈R，λ1∈R，终止误差0≤ε≤1，σ1>0，ϑ∈(0,1)，η>1，令k=1；

2) 以wk-1为初始条件，求解无约束子问题

得到极小点wk；

3) 若‖(wHe-1)‖2≤ε，停止运算，输出w*=wk作为原问题的近似极值点，否则转向下一步；

4) 令λK+1=λK-σk(wHe-1)；

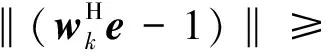
6) 令k=k+1，转向步骤2继续找极值点直到结束。

4 实验过程与分析

本研究成像算法的实验模型与平台如图2所示，测试对象为500 mm×300 mm×3 mm的铝板，在铝板表面布置了5个PZT传感器，直径为10 mm，用来发送和接受导波信号。理论上为了形成传感器网络，可以使用大量的传感器配置成致密网络来获取更多的冗余信号，达到更加可靠的效果，然而对于工程应用是不实际的。可以利用一些传感器优化配置的算法实现布局优化，但是许多优化后的布置位置由于结构自身原因不便于安装传感器。为了检测成像效果的有效性，提高实用性，本实验配置为图3所示的稀疏网络阵。铝板尺寸为500 mm×300 mm，5个PZT的坐标位置分别为(125,150)，(260,200)，(305,285)，(390,130)，(390,30)mm，缺陷为一个直径为5 mm的通孔，位置为(250,140)mm。

图2 实验模型与平台Fig.2 Experimental model and platform

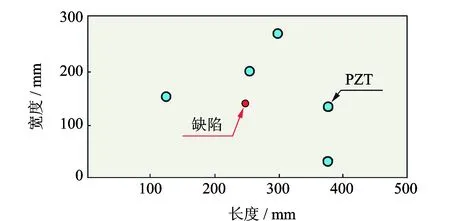
图3 铝板尺寸及PZT、缺陷位置Fig.3 Aluminum plate size and PZT, defect location

实验过程中，首先利用Tek AFG3102函数信号发生器产生5个周期的正弦信号，经过汉宁窗调制后依次加载到各PZT上，这样可以产生10路信号。利用Tek MSO4045B示波器采集并记录数据，实验前先进行多次采样，平均后得到健康信号作为后续分析的基准信号，图4为PZT1-2路归一化的基准信号。在缺陷位置处钻5 mm通孔形成板材上的缺陷，然后采集记录缺陷信号，图5为PZT1-2路归一化的缺陷信号。为了降低噪声和比对相对幅值，本实验中对基准信号和缺陷信号都做了小波降噪和归一化处理。两种信号做减运算后进行Hilbert变换突出缺陷特征，得到图6所示的归一化包络信号。包络信号中含有缺陷的位置、形态信息，利用包络信息计算像素点值，从而构造出铝板的成像。图7为算法直接成像，从图中可以看出，图像中含有较多的噪点和干扰，成像效果较差，其主要原因为PZT5比较靠近铝板的边界，边界反射对接收信号造成了干扰。图8为PH乘子算法的成像优化，可以从图中看到，含有较少的噪点，缺陷处的成像与实际位置相符，位置准确度较高，成像质量明显得到提高。然而由于边界反射的原因，缺陷区域没有较好地反映出缺陷孔的几何特征。

图4 1-2路归一化基准信号Fig.4 Normalized reference signal of 1-2 path

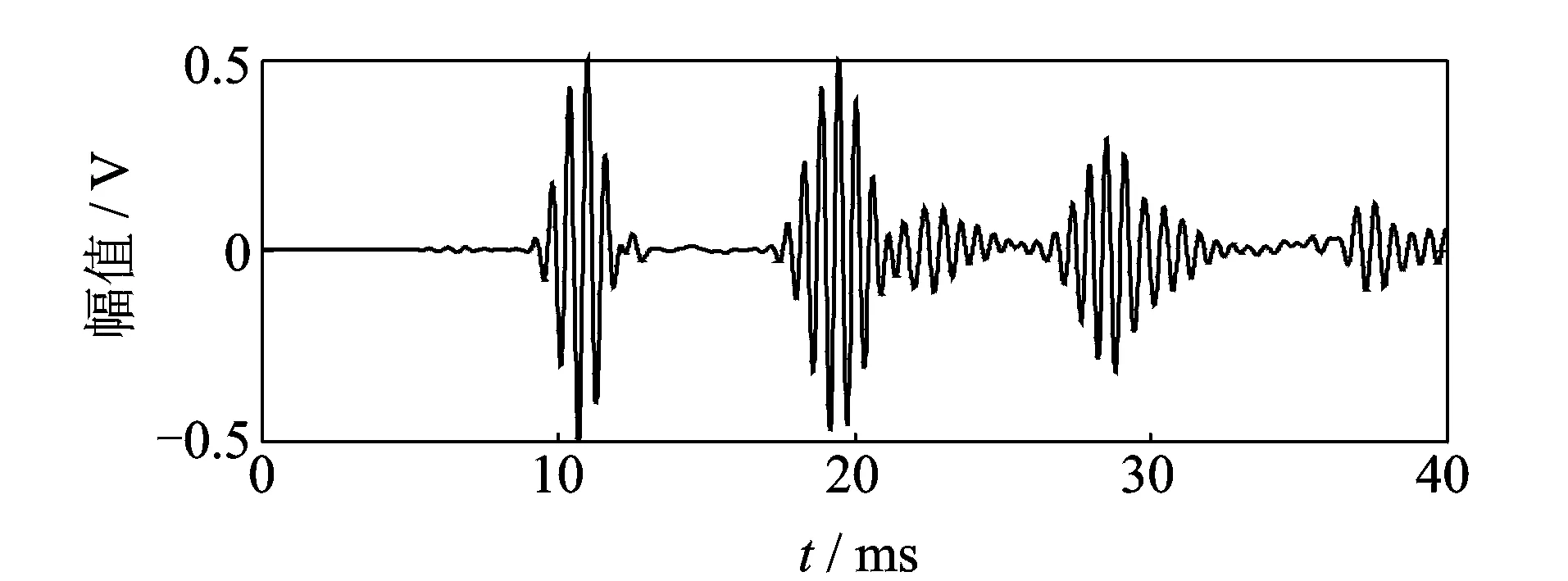
图5 1-2路归一化缺陷信号Fig.5 Normalized defect signal of 1-2 path

图6 1-2路差值信号包络Fig.6 Difference signal envelope of 1-2 path

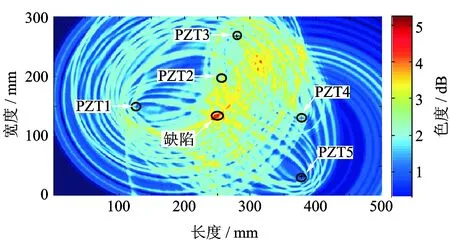
图7 直接成像Fig.7 The result of direct imaging

图8 PH乘子算法的成像优化Fig.8 The result of PH multiplier imaging optimization

5 结束语

在分析导波缺陷定位成像原理的基础上，将包络幅值位置响应的方法应用到导波检测中，引入了包含有位置权重矢量的成像算法以突出缺陷像素点的特征。应用PH乘子算法的成像优化实现了权重矢量优化，在保证所需要方向信号不变的情况下，实现了对板中缺陷图像的重构，是对传统算法的扩展和改进。该方法能够较为清晰、准确地表征损伤的发生区域和程度，提高了成像的质量。然而，从实验中发现边界反射影响了成像质量，今后研究工作中将运用多目标优化的算法，既要合理地消除边界反射影响，又要在成像中反映缺陷形状特征，完善导波检测成像算法。

参 考 文 献

[1] 何存富, 周文桢, 刘增华,等. 基于多通道时间反转Lamb波的铝板小缺陷检测[J]. 实验力学, 2015, 30(6): 683-689.

He Cunfu, Zhou Wenzhen, Liu Zenghua, et al. Small-sized defect detection in aluminum plate based on time reversal lamb waves[J]. Journal of Experimental Mechanics, 2015, 30(6): 683-689. (in Chinese)

[2] Huang Pingping, Yao Yuanwei, Wu Fugen, et al. Interface-guided mode of Lamb waves in a two-dimensional phononic crystal plate[J]. Chinese Physics B, 2015(5): 404-409.

[3] 刘增华, 樊军伟, 何存富,等. 基于概率损伤算法的复合材料板空气耦合Lamb波扫描成像[J]. 复合材料学报, 2015, 32(1): 227-235.

Liu Zenghua, Fan Junwei, He Cunfu, et al. Scanning imaging of composite plate using air-coupled lamb waves based on probabilistic damage algorithm[J]. Acta Materiae Compositae Sinica, 2015, 32(1): 227-235. (in Chinese)

[4] 杜云朋, 王建斌, 张轩硕,等. 基于改进PSO算法的LS-SVM对管道超声导波缺陷的二维轮廓重构[J]. 机械科学与技术, 2014, 33(9): 1350-1353.

Du Yunpeng, Wang Jianbin, Zhang Xuanshuo, et al. 2D profile reconstruction of defect in pipe ultrasonic guided wave based on LS-SVM with improved PSO algorithms[J]. Mechanical Science and Technology for Aerospace Engneering, 2014, 33(9): 1350-1353. ( in Chinese)

[5] Seher M, Huthwaite P, Lowe M J S, et al. Model-based design of low frequency Lamb wave EMATs for mode selectivity[J]. Journal of Nondestructive Evaluation, 2015, 34(3): 22.

[6] Velichko A, Wilcox P D. Post-processing of the full matrix of ultrasonic transmit-receive array data for guided wave pipe inspection[J]. Aip Conference Proceedings, 2009, 1096(1): 137-144.

[7] Yu L, Leckey C A. Lamb wave-based quantitative crack detection using a focusing array algorithm[J]. Journal of Intelligent Material Systems & Structures, 2013, 24(9):1138-1152.

[8] Yu L, Giurgiutiu V. Piezoelectric wafer active sensors in lamb wave-based structural health monitoring[J]. Jom the Journal of the Minerals Metals & Materials Society, 2012, 64(7): 814-822.

[9] Yu L, Bottai-Santoni G, Giurgiutiu V. Shear lag solution for tuning ultrasonic piezoelectric wafer active sensors with applications to Lamb wave array imaging[J]. International Journal of Engineering Science, 2010, 48(48): 848-861.

[10] 张海燕, 马世伟, 冯国瑞,等. 兰姆波结构健康监测中的概率损伤成像[J]. 声学学报, 2012, 7(4): 401-407.

Zhang Haiyan, Ma Shiwei, Feng Guorui, et al. Probability damage imaging in lamb wave structural health monitoring[J]. Acta Acustica, 2012, 7(4): 401-407. (in Chinese)

[11] Hettler J, Tabatabateipour M, Delrue S, et al. Application of a probabilistic algorithm for ultrasonic guided wave imaging of carbon composites[J]. Physics Procedia, 2015, 70: 664-667.

[12] 刘彬, 邱雷, 袁慎芳,等. 复合材料T型接头损伤监测的概率成像方法[J]. 振动、测试与诊断, 2015，35(3):519-524.

Liu Bin, Qiu Lei, Yuan Shenfang, et al. The probability imaging algorithm of composite T-joint damage monitoring[J]. Journal of Vibration, Measurement & Diagnosis, 2015，35(3):519-524. (in Chinese)

[13] 孙汝杰, 陈国平, 孙东阳,等. 核密度估计法在板件概率损伤识别中的应用[J]. 振动、测试与诊断, 2015，35(6):1055-1062.

Sun Rujie, Chen Guoping, Sun Dongyang, et al. Probabilistic damage detection based on the kernel density estimation method in aluminum plates[J]. Journal of Vibration, Measurement & Diagnosis, 2015，35(6):1055-1062. (in Chinese)

[14] Li Mingliang, Deng Mingxi, Gao Guangjian. Modal expansion analyses of ultrasonic Lamb waves generated by electromagnetic ultrasonic transducers[J]. Shengxue Xuebao/Acta Acustica, 2014, 39(3): 385-391.

[15] 张宇, 闫云聚, 余龙,等. CSM在基于Lamb波的结构损伤检测中的应用[J]. 工程力学, 2015(6): 22-27.

Zhang Yu, Yan Yunju, Yu Long, et al. Application of CSM in Lamb wave based on structural damage detection[J]. Engineering Mechanics, 2015(6): 22-27. (in Chinese)

[16] 李富才, 彭海阔, 孙学伟,等. 基于谱元法的板结构中导波传播机理与损伤识别[J]. 机械工程学报, 2012, 48(21): 57-66.

Li Fucai, Peng Haikuo,Sun Xuewei, et al. Guided wave propagation mechanism and damage detection in plate structures using spectral element method[J]. Journal of Mechanical Engineering, 2012, 48(21): 57-66. (in Chinese)

[17] Pateros C N, Saulnier G. An adaptive correlator receiver for direct-sequence spread-spectrum communication[J]. Communications IEEE Transactions on, 1996, 44(11): 1543-1552.

[18] Yoon Y S, Amin M G, Ahmad F. MVDR Beamforming for through-the-wall radar imaging[J]. IEEE Transactions on Aerospace Electronic Systems, 2011, 47(1): 347-366.

[19] 白云娇. 带目标罚参数的精确罚函数法[D].重庆：重庆大学, 2014.