飞机部件数字化调姿定位测量点的优选与构造算法

巴晓甫，薛红前，李西宁

1. 西北工业大学 机电学院，西安 710072

2. 中航西安飞机工业集团股份有限公司 制造工程部，西安 710089

数字化调姿定位系统中飞机部件的位姿常通过固连在部件上的测量点的坐标来控制，依据测量点在调姿定位前的实际坐标和调姿定位后的理论坐标将飞机部件从初始位姿调整到目标位姿。然而由于飞机部件的弱刚性、装配应力的释放、运输过程的振动、受力状态的改变、以及制造误差和测量误差等因素，导致实际工况中各个测量点之间的实际长度与理论长度存在偏差，甚至存在超差。如果在调姿定位前不对测量点及其坐标数据进行处理，在调姿定位过程中将产生较大的系统内力，并将影响飞机部件的调姿定位精度。

测量点坐标数据的采集设备主要有：激光跟踪仪、激光雷达、IGPS (Indoor GPS)、视觉测量等，其中，由于激光跟踪仪在大尺寸测量场中具有较高精度，使之在飞机数字化调姿定位中应用最为广泛。测量点坐标数据在初始位姿与目标位姿的配准方法，常见的有奇异值分解法 (Singular Value Decomposition, SVD)、正交矩阵法、四元数法、线性子空间法、双四组元法等。张宪朝以固连在某中机身壁板上的测量点为研究对象，采用加权后的奇异值分解法对测量点坐标进行点到点的拟合匹配，建立了加权拟合后的变换矩阵，但该变换矩阵经加权处理后不具备正交变换特性，测量点之间的距离在变换前后发生了改变。朱绪胜和郑联语采用奇异值分解法对两个坐标系统中的某卫星部件的测量点进行空间配准，然后依据装配关键特性中相关公差的重要程度，以最小综合偏差为优化目标求解测量点的匹配坐标。这种将所有测量点都纳入拟合计算的方法，难以适用某些点发生了严重超差的情况。雷沛和郑联语采用几何特征结合奇异值分解方法对某飞机垂尾测量点进行拟合，但是该研究只针对测量点分布在一条直线或一个平面上的几何特征的情况。王青等建立了固连在高刚度三坐标定位器上的测量点的拟合匹配方法，采用序列二次规划 (Sequential Quadratic Programming, SQP)优化方法对测量点的匹配构造进行求解，但是该方法不适用于弱刚度工件上测量点的拟合处理。Devendeville等将飞机大部件对接公差约束问题转化为构建测量点最佳拟合(Best Fit，BF)数学模型的问题，但没有考虑测量点中坏点的处理。王巍等将某客机翼身对接系统测量点的实测坐标和理论坐标直接输入给半数字化调姿定位系统(三坐标定位器轴和轴为随动轴，只有轴为主动轴)，该方法没有考虑测量点之间距离的测量值与理论值的差异，如果用于全数字驱动的调姿定位系统将带入较大的系统内力，也难以获得较高的调姿定位精度。朱永国等研究了飞机装配测量场中布设的公共测量点的数量与测量场控制精度的关系。Traslosheros 等提出了一种基于单相机采集测量点位置信息的并联机器人运动参数校准的方法。Mei等提出了一种基于多个测量点的移动制孔机器人基坐标系的二维视觉标定方法。王志浩等以飞机自动钻铆调姿托架及其测量点为研究对象，研究了基于约束微分方程的误差模型，建立了工件位姿误差与调姿定位器结构误差的关系表达式。李玉昆等以3-UPS/S数字化调姿平台及其测量点为研究对象，构建了调姿平台几何误差与受力之间的传递函数，并基于传递模型建立了调姿平台在满载情况下的运动学位姿求解和标定模型。Ni等针对全圆旋转机械手，在基于空间矢量链的误差映射模型和参数识别的基础上,采用基于双靶球的测量方式，通过建立测量数据和误差数据之间的映射关系，实现了并联机构的运动学标定。Bi等通过优化壁板荷载传递与定位器位移的关系，建立了基于偏最小二乘回归方法的弱刚度机身壁板的测量点位置偏差与三坐标调姿定位器位移的模型，通过定位器对壁板的主动施力达到壁板校形的目的，以实现测量点的位置精度，该方法适用于提高弱刚度工件的调姿定位精度。由于测量点偏差的校正需要调姿定位系统主动的施加额外作用力，因而系统隐含着一定的安全风险。Fang等设计了一种用于飞机翼身装配变形校正的力位混合控制系统，将冗余驱动并联机构中的六个运动轴设置为位置控制，其它运动轴设置为力控制，通过主动施加校形力，强迫翼身变形以实现固连在翼身的测量点的位置精度。上述工作为飞机部件的数字化调姿定位提供了理论模型和技术手段。

然而，目前针对飞机数字化装配中的测量点的研究，主要集中于飞机部件或者工装设备的位姿拟合与标定，以及变形校正，虽然得到了较高的精度，但测量点之间的距离也发生了变化。对于飞机部件数字化调姿定位，不仅需要关注调姿定位前后的位姿精度——将飞机部件从初始位姿精确地调整到目标位姿，还需要关注调姿定位过程中系统内力随时间的变化情况，确保系统内力保持稳定，并关注系统内力带入的安全风险：当调姿定位系统直接与飞机部件连接时，系统内力将给飞机部件和系统本身带入安全风险；当调姿定位系统通过整体工艺托架与飞机部件连接时，系统内力将给整体工艺托件和系统本身带入安全风险。

为提高飞机部件数字化调姿定位的整体精度，降低调姿定位过程中的系统内力,提出一种测量点的优选和构造算法，以固连在飞机部件上的测量点的位置坐标及其公差作为输入条件，分析测量点的位置偏离状态，对测量点进行优选，并对优选测量点进行匹配构造，使构造点处于其理论点的公差盒内，并使构造点与理论点的偏差平方和最小，以实现飞机部件的准确调姿定位。

1 飞机部件数字化调姿定位工艺

以某飞机壁板为例介绍飞机部件数字化调姿定位工艺。某飞机壁板由蒙皮和长桁组成，在壁板调姿定位中，壁板内型须与翼肋外型贴实，如果采用测量点数据调装的方法，壁板内型与翼肋外型将有大量的加垫和打磨工作量，装配质量也难以保证。工程上，一般通过提高壁板和翼肋的制造精度，将壁板内型与翼肋外型贴实，通过尺寸链的方式间接保证壁板的外形精度。因此，本文仅采集布置在壁板周边的18个测量点，用来控制壁板4条边的位姿状态，如图1所示。通过将壁板与翼肋贴实和调整四条边的位姿状态实现壁板的调姿定位。

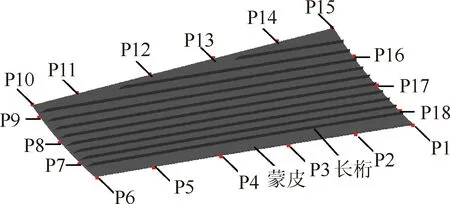
图1 某飞机壁板及其固连的测量点Fig.1 Aircraft panel and its fix together measuring points

飞机壁板的制造工艺流程如图2所示，根据设计定义的数据，利用钻模板在壁板上精确地钻出测量点所依附的圆孔，并将圆孔轴线与壁板外型面的交点定义为测量点的位置。测量点将作为壁板调姿定位和精度检测的依据。

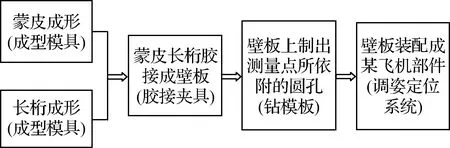
图2 某飞机壁板制造工艺流程Fig.2 Aircraft panel manufacturing process

调姿定位系统由4台随位并联的三坐标定位器组成，分别为PT1、PT2、PT3、PT4。三坐标定位器由运动轴、运动轴、运动轴、末端球窝及其抱紧机构组成，如图3所示。每台三坐标定位器的3个运动轴均为伺服驱动轴。为减少调姿定位的机械误差，每个伺服驱动轴均配置了HEIDENHAIN-LC483光栅尺以实现全闭环控制。三坐标定位器的末端球窝与整体工艺托架的球头相配合构成球铰副。末端球窝的底部设置了HEIDENHAIN-MCS10三分位力传感器，用来感知三坐标定位器与整体工艺托架之间的相互作用力(系统内力)。调姿定位系统通过4个球铰副支撑整体工艺托架。壁板经吊装放置在整体工艺托架上，并通过真空吸附装置将壁板与整体工艺托架固定。

图3 某飞机壁板调姿定位系统Fig.3 Attitude adjustment and positioning system of aircraft panel

2 测量点优选与构造算法

对于飞机部件调姿定位的整体精度而言，测量点在满足包络飞机部件前提下，可以均匀分布、特定分布，也可以随机分布。测量点优选与构造算法的流程如图4所示。

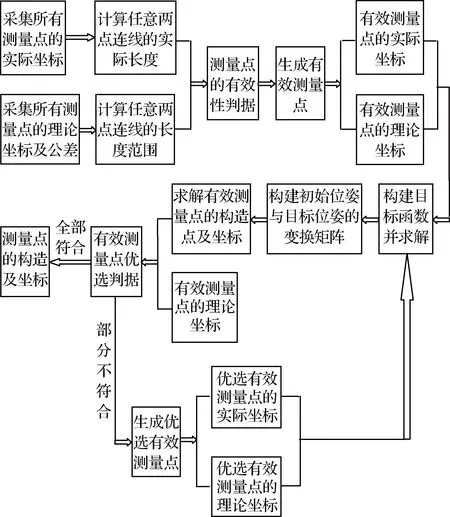
图4 测量点优选与构造算法流程Fig.4 Algorithm flow of optimization and construction for measuring points

图5所示为飞机壁板及其固连的测量点，测量点的数量不少于4个，图5左壁板是调姿定位前壁板相对于参考坐标系所处的位姿状态，图5右壁板是调姿定位后壁板需要调整到的相对于参考坐标系的理论位姿状态。

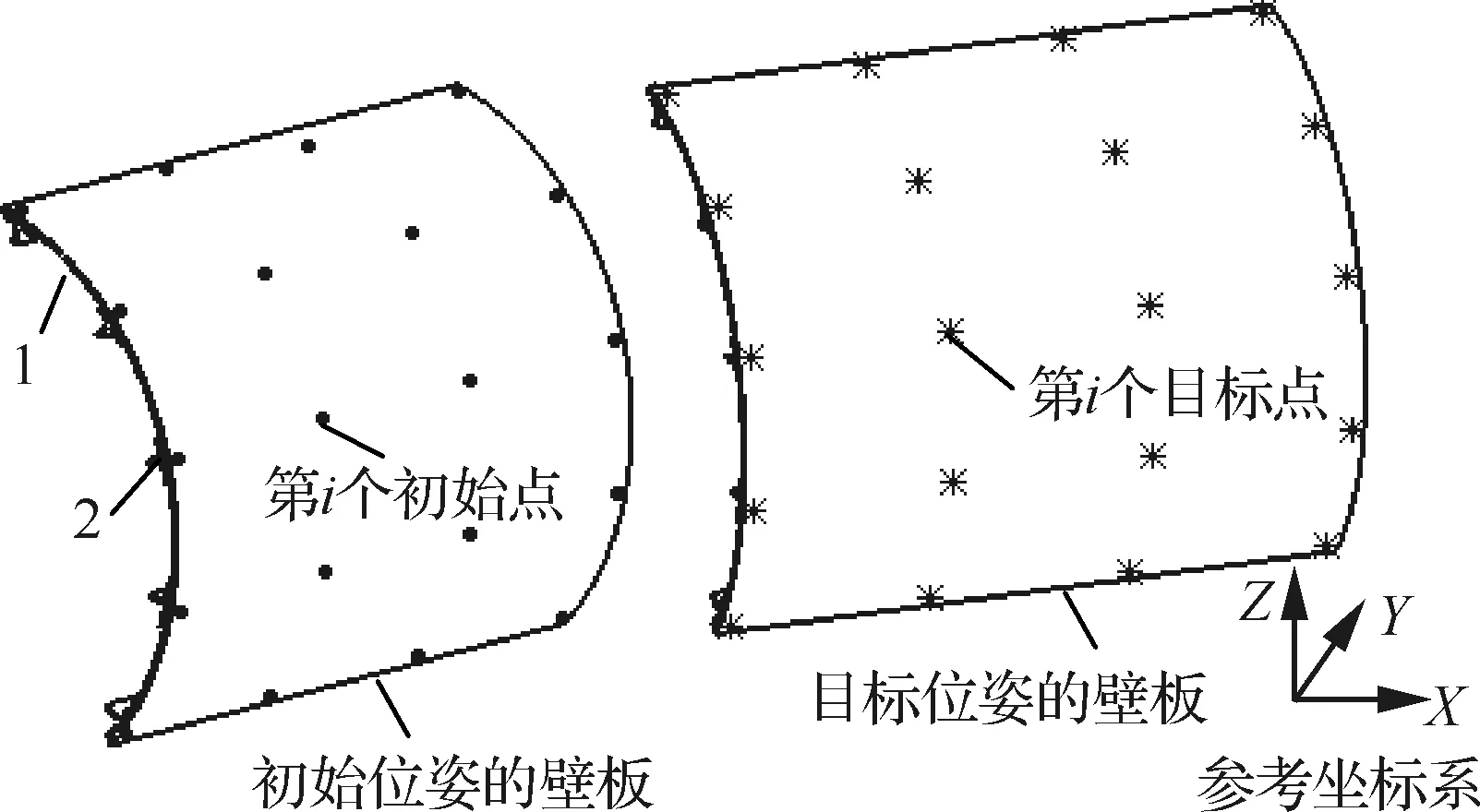
图5 飞机壁板及其固连的测量点Fig.5 Aircraft panel and measuring points fixed on aircraft panel

通过坐标测量设备，获得调姿定位前壁板上固连测量点的初始点相对于参考坐标系的实际坐标：

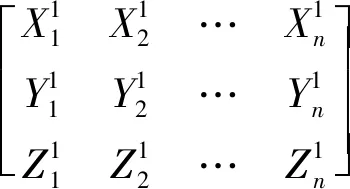
(1)

式中:≥4。

通过设计信息或者工艺信息，获得调姿定位后壁板上固连测量点的目标点相对于参考坐标系的理论坐标及其公差：

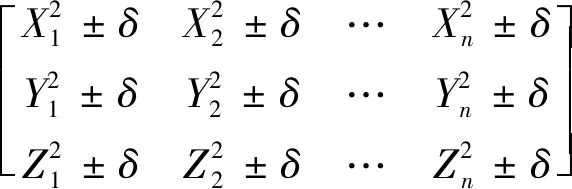
(2)

式中:为测量点的位置公差，>0该值由飞机产品设计确定。

首先，求解任意两个测量点连线的实际长度：

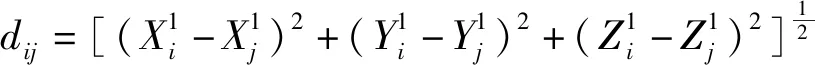
(3)

式中:≠,≥≥1,≥≥1。

然后,求解任意两个测量点连线的理论长度：

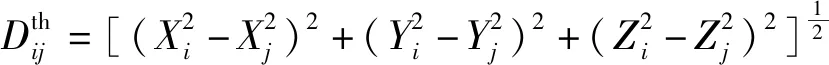
(4)

接着,构建任意两个测量点连线所允许的长度范围：

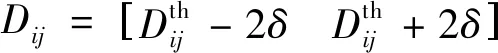
(5)

最后，构建测量点的有效性判据：

∈

(6)

对式(3)～式(5)按与的取值范围计算，找出不满足式(6)判据要求次数最多的第个测量点，并将该测量点剔除掉。重复式(3)～式(5)的计算以及按式(6)判据剔除不符合要求的测量点，直至所有测量点满足式(6)为止。如图6所示，将不符合有效性判据的测量点剔除掉。

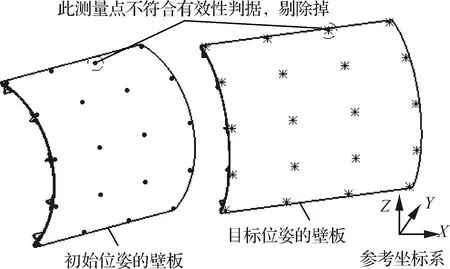
图6 不符合有效性判据的测量点示意Fig.6 Indications of measuring points that do not meet validity criteria

将满足式(6)的测量点筛选出来，组成有效测量点，获取有效测量点的初始点相对于参考坐标系的实际坐标：

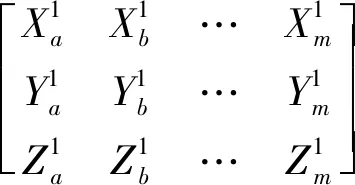
(7)

式中:≥>>≥1。

获取有效测量点的目标点相对于参考坐标系的理论坐标：

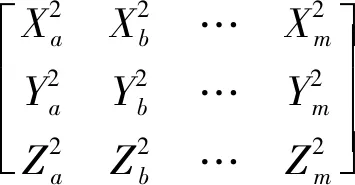
(8)

构建目标函数，并求解目标函数取得最小值时未知量的解：

(9)

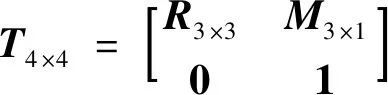
(10)

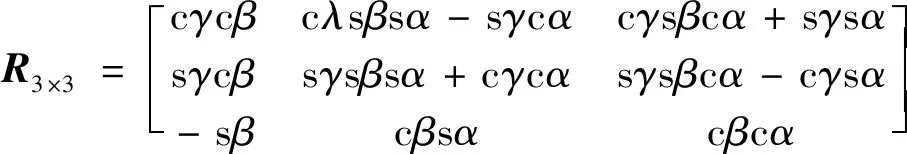
(11)

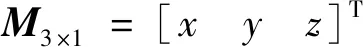
(12)

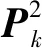
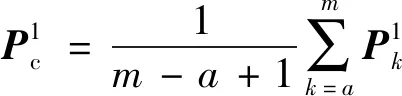
(13)

所有有效测量点的目标点的形心相对于参考坐标系的坐标为

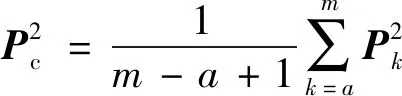
(14)

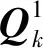
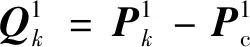
(15)

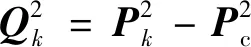
(16)

构建协方差矩阵:

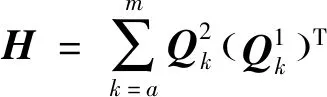
(17)

对进行奇异值分解：

=

(18)

式中：为左奇异矩阵，为右奇异矩阵，和均为正交矩阵；为对角阵。

依据式(11)和式(12)，可得

=

(19)

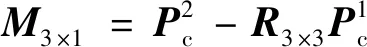
(20)

求解得到壁板初始位姿与目标位姿的变换矩阵及其6个变量。

通过式(10)变换矩阵，将有效测量点的初始点变换为有效测量点的构造点，获得目标位姿处有效测量点的构造点相对于参考坐标系的坐标。如图7所示，圆形点所示为有效测量点的构造点相对于参考坐标系的位置：

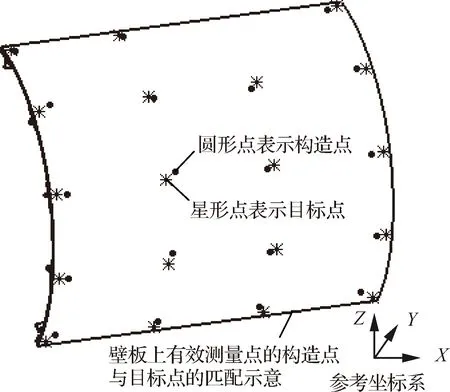
图7 有效测量点的构造点与目标点在参考坐标系下的匹配示意Fig.7 Matching diagram between construction points and target points of effective measuring points in reference coordinate system

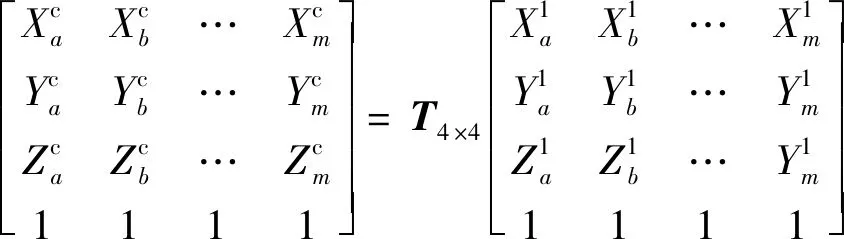
(21)

求解目标位置处有效测量点的构造点与目标点的位置偏离值，图8为有效测量点的构造点与目标点的位置偏离示意，构造点坐标偏差为

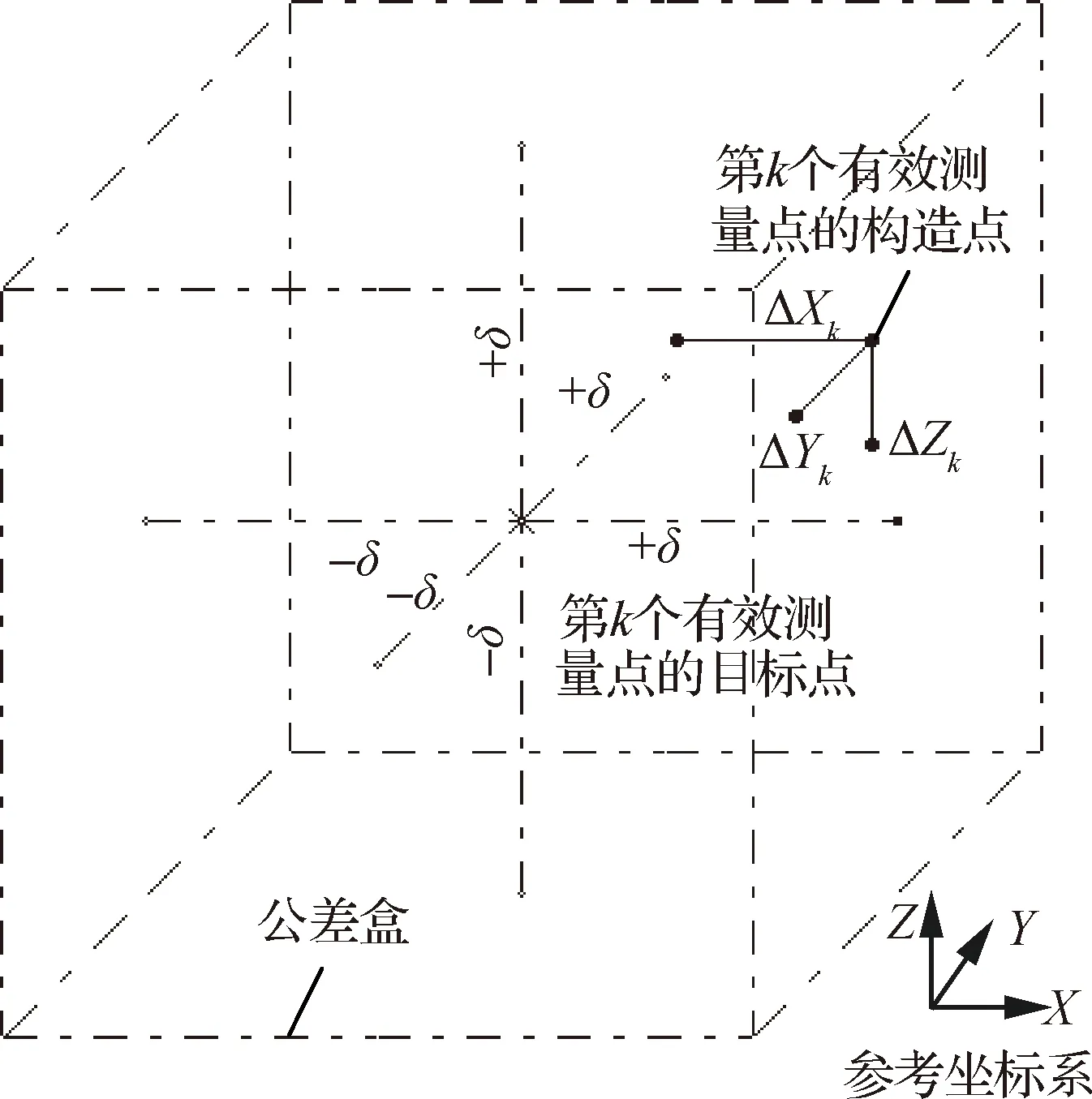
图8 壁板上第k个测量点的构造点与目标点的偏离示意Fig.8 Deviation diagram between construction point and target point of the kth measuring point fixed on aircraft panel

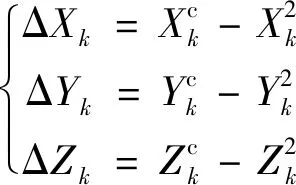
(22)

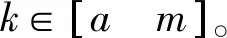
构造有效测量点的优选判据：

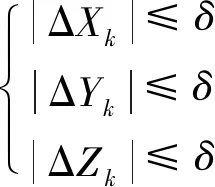
(23)

有效测量点的目标点的位置及其公差盒如图8 所示。

将满足式(23)的有效测量点筛选出来，组成优选有效测量点，获取优选有效测量点对应的初始点相对于参考坐标系的坐标：

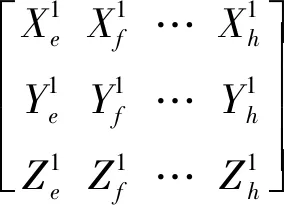
(24)

式中:≥≥>>≥≥1。

如图9所示，星形点表示优选有效测量点的目标点的位置，圆形点表示优选有效测量点的构造点的位置。

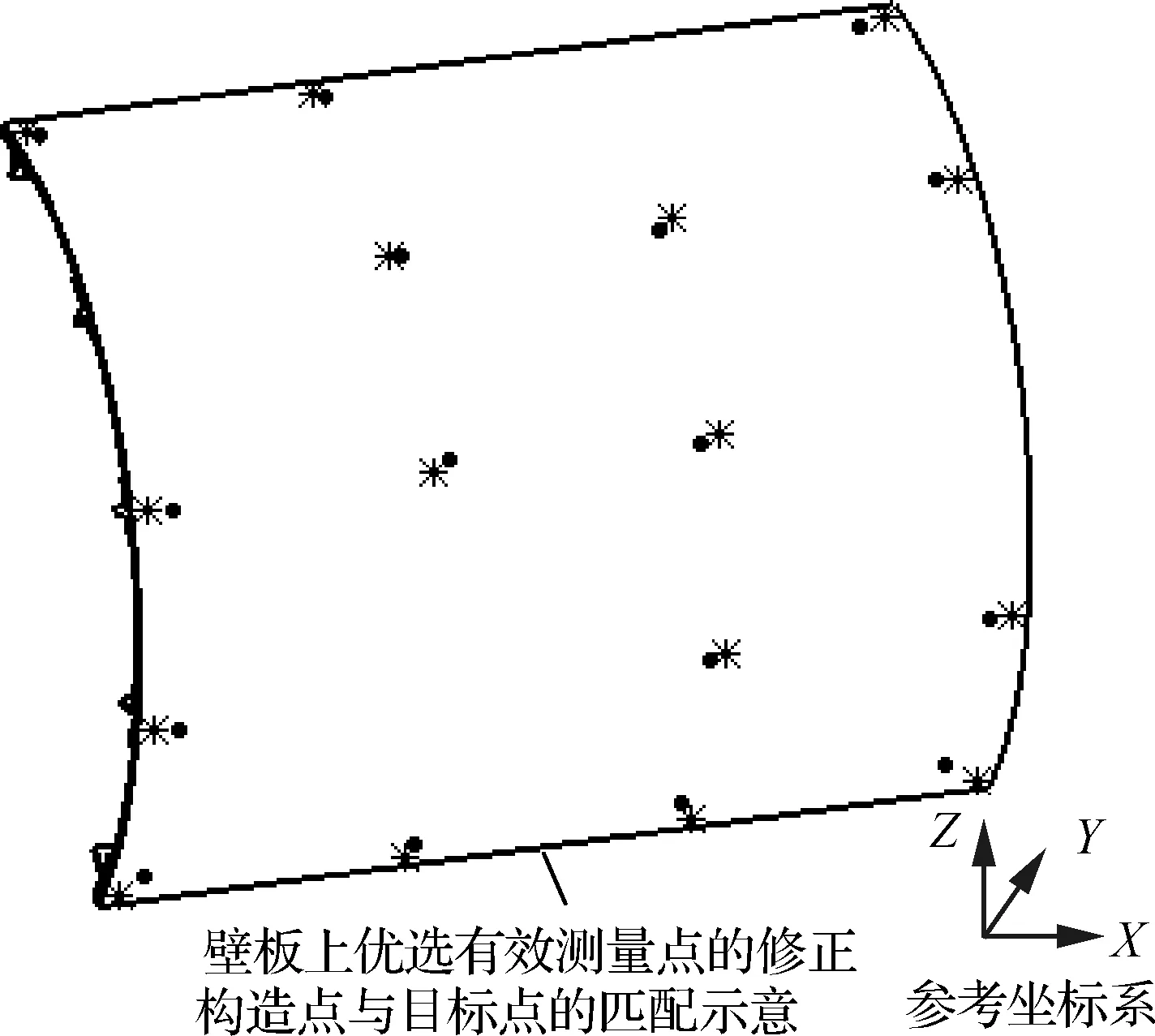
图9 优选有效测量点的修正构造点与目标点的匹配Fig.9 Matching of modified construction points and target points of preferred effective measuring points

再次构建目标函数，并求解函数取得最小值时未知量的解：

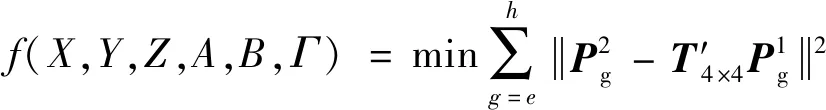
(25)

式中：、、分别为壁板沿参考坐标系轴、轴、轴的平移距离;、、分别为壁板绕参考坐标系轴、轴、轴的旋转角度。

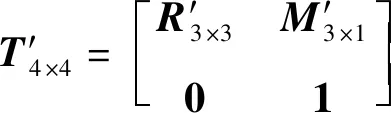
(26)

′=

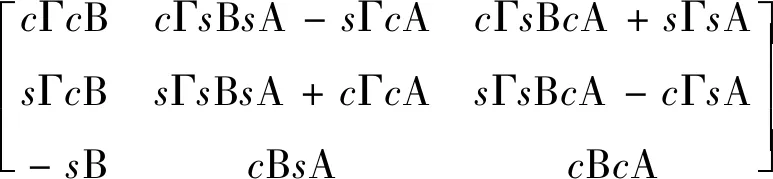
(27)

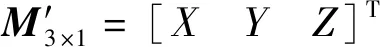
(28)

通过计算测量点的形心化坐标和构建协方差矩阵以及奇异值分解法(SVD)，可求解出正交旋转矩阵′、平移向量′、修正变换矩阵′，以及6个变量。

通过式(26)修正变换矩阵，将优选有效测量点的初始点修正变换为优选有效测量点的构造点，获得目标位置处优选有效测量点的构造点相对于参考坐标系的坐标：

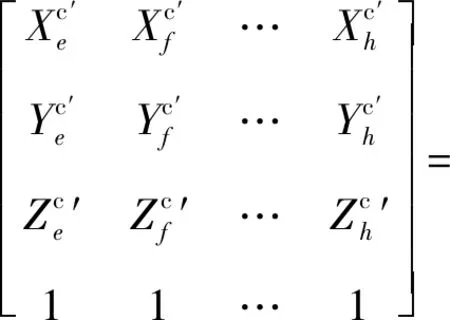
(29)

3 试验与应用分析

基于第1节所述的飞机壁板、调姿定位工艺及其调姿定位系统，开展测量点优选与构造算法的试验验证与应用分析。实物系统如图10所示。

图10 调姿定位系统实物Fig.10 Physical object of attitude adjustment and positioning system

飞机壁板制造处于图2所示的第4步调姿定位工序时，壁板及其固连的测量点与调姿定位系统的布局图如图11所示。首先调整4个三坐标定位器末端球窝的位置，使4个球铰副内力的铅垂分力接近相等，水平分力接近为零。将该状态定义为壁板的初始位姿状态，通过Leica-AT960激光跟踪仪测量获得所有测量点的初始点相对于飞机坐标系的实际坐标，如表1所示。所有测量点的目标点相对于飞机坐标系(以飞机坐标系为参考坐标系)的理论坐标及其公差由飞机设计定义，如表2所示。由于壁板的弱刚性、装配应力的释放、运输过程中的振动、受力状态的改变、制造误差和测量误差等因素，使得两组数据中任意两个对应的测量点之间的长度都不会相等。

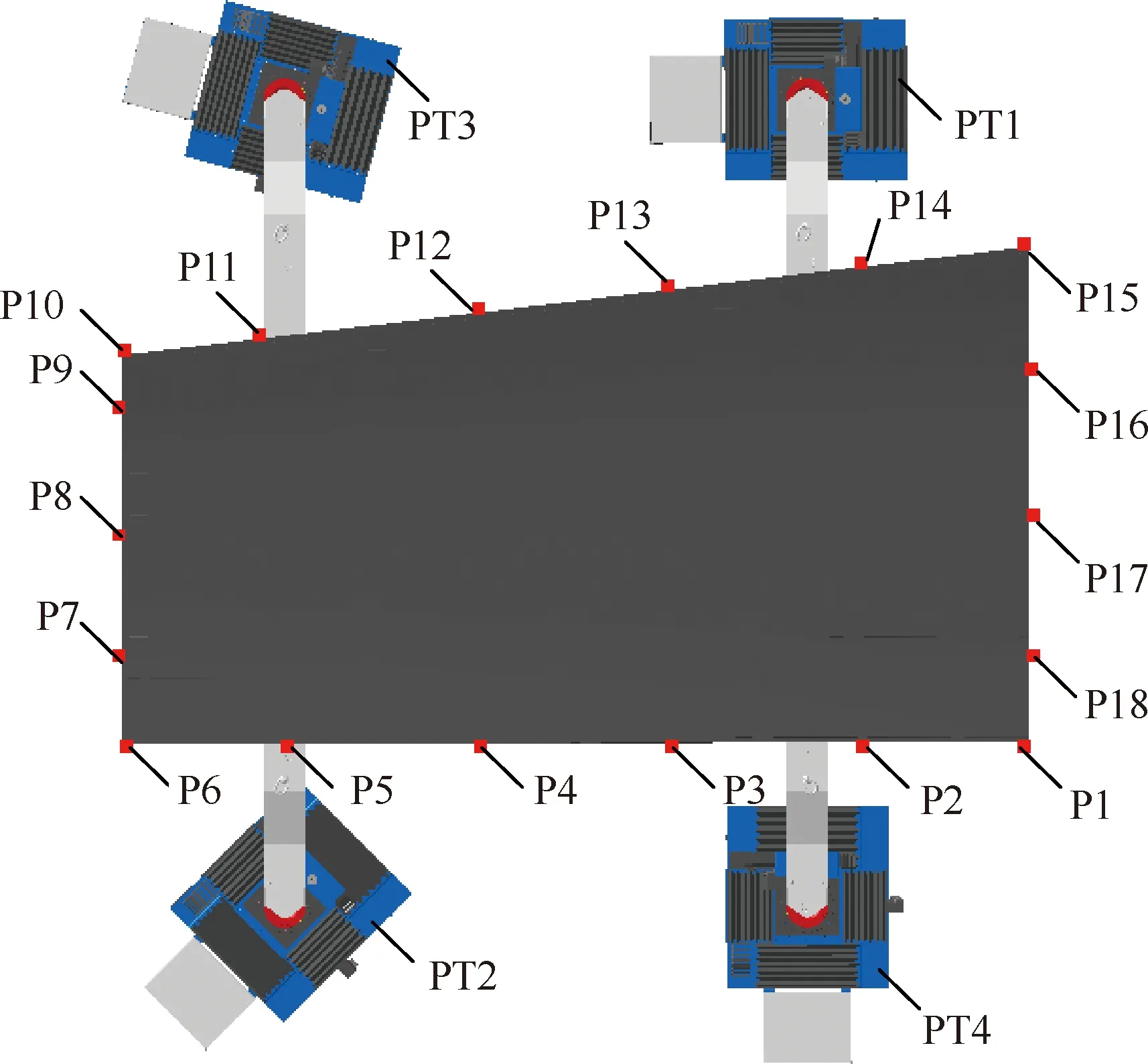
图11 壁板测量点及其调姿定位系统布局图Fig.11 Layout diagram of panel measuring points and attitude adjustment and positioning system

3.1 测量点无优选和构造

将表1和表2测量点的坐标数据分别作为调姿定位系统运动算法中壁板初始位姿和目标位姿时测量点的输入数据，设置调姿定位的时间为100 s，通过运动学算法，得到各个伺服轴的运动学参数与时间的关系。

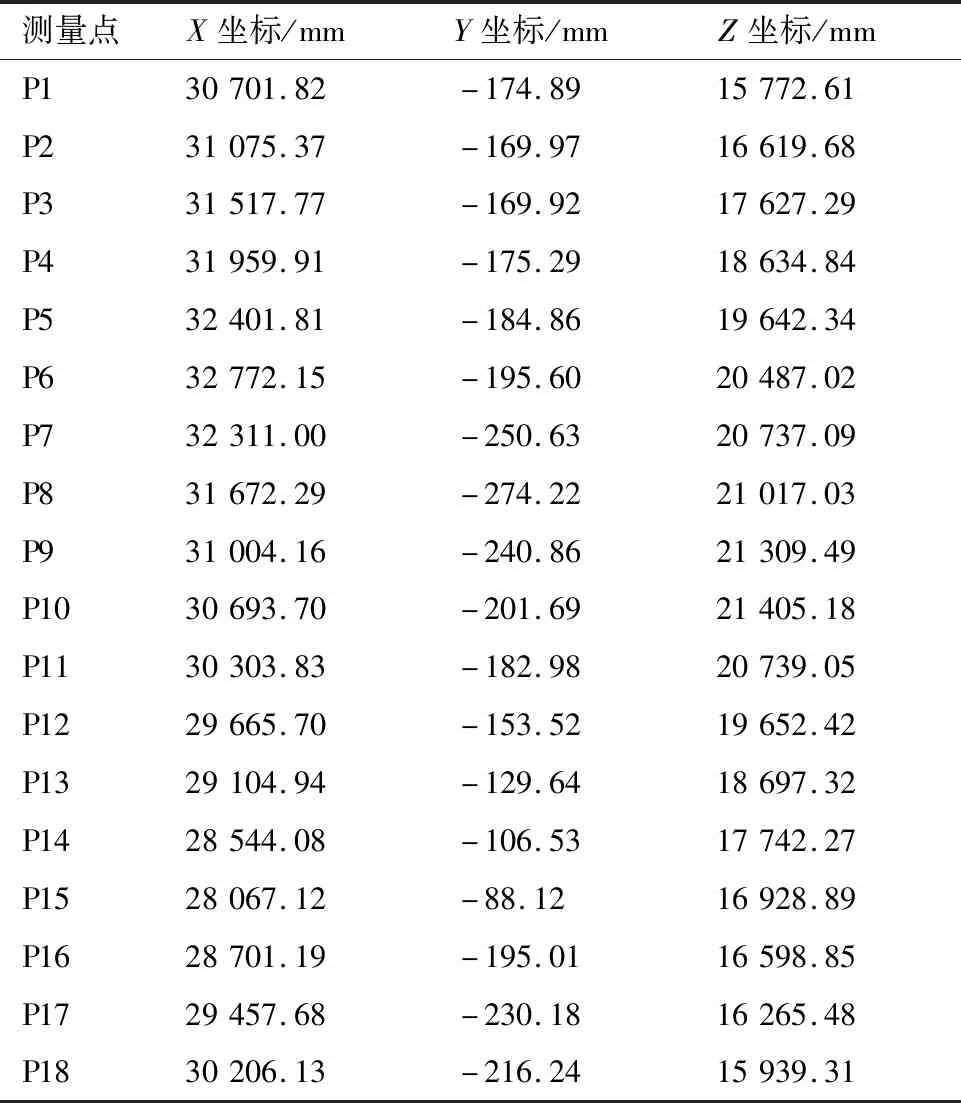
表1 所有测量点的初始点相对于飞机坐标系的实际坐标Table 1 Actual coordinates of all initial measuring points relative to aircraft coordinate

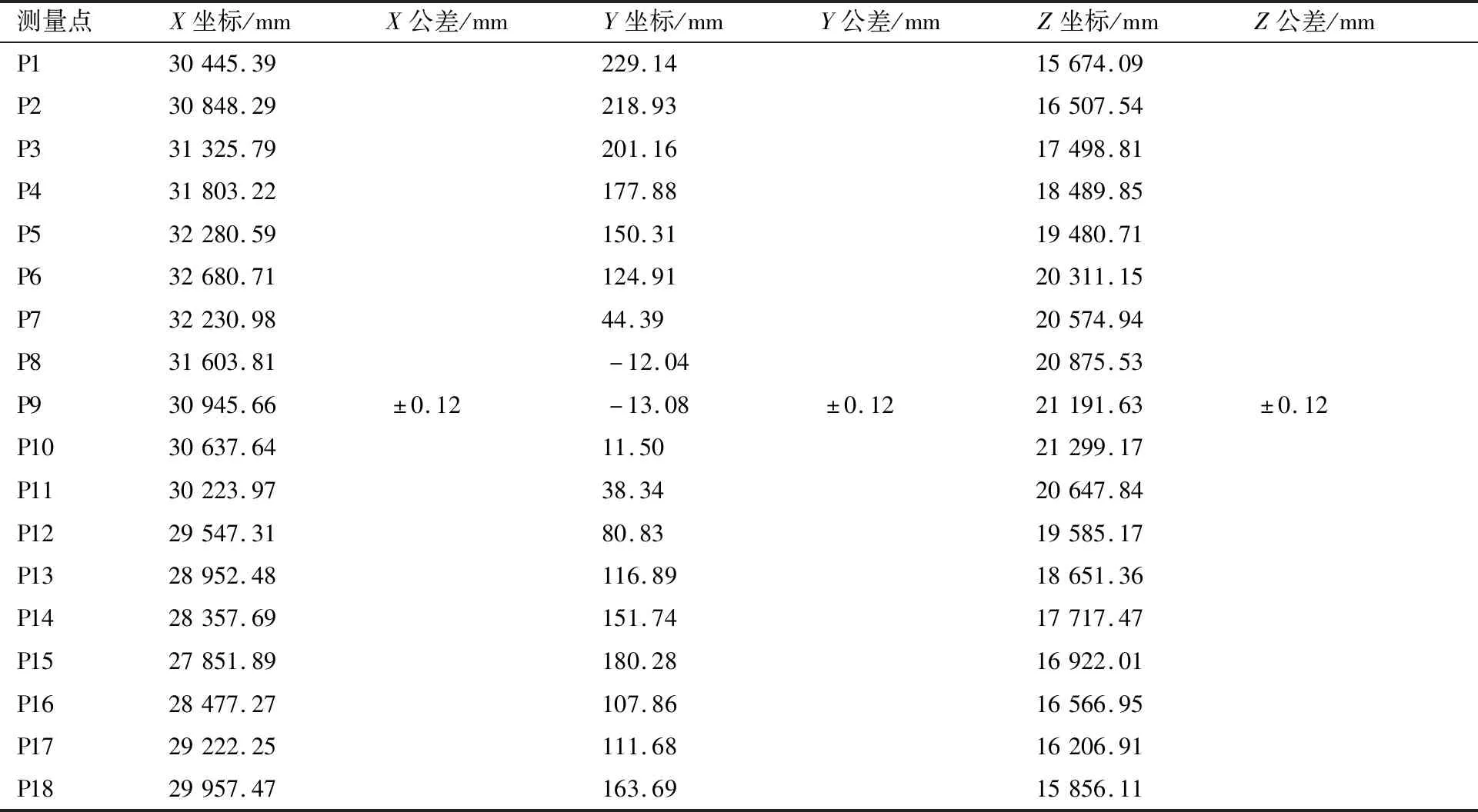
表2 所有测量点的目标点相对于飞机坐标系的理论坐标及其公差Table 2 Theoretical coordinates and its tolerances of all target measuring points relative to aircraft coordinate system

壁板在调姿定位过程中，通过三分位力传感器，记录4个球窝所受水平分力随时间的变化曲线，如图12所示。从图中可以看出，4台三坐标定位器球窝的水平内力均随时间而不断增大，当调姿定位结束时，内力达到最大值，其中水平内力最大的三坐标定位器为PT1，达到2 764.9 N，最小的为PT3，达到1 416.8 N。造成调姿定位系统在运动过程中产生内力的原因是由于固连在壁板上的测量点之间的长度发生了变化，调姿定位系统通过球铰副对整体工艺托架施加作用力，试图使整体工艺托架上的壁板变形以实现测量点之间连线的变化。因此可以看出，如果调姿定位前后两个测量点连线的长度发生变化，调姿定位系统的内力就会增大，就存在损伤整体工艺托架和调姿定位系统甚至人员的安全风险。

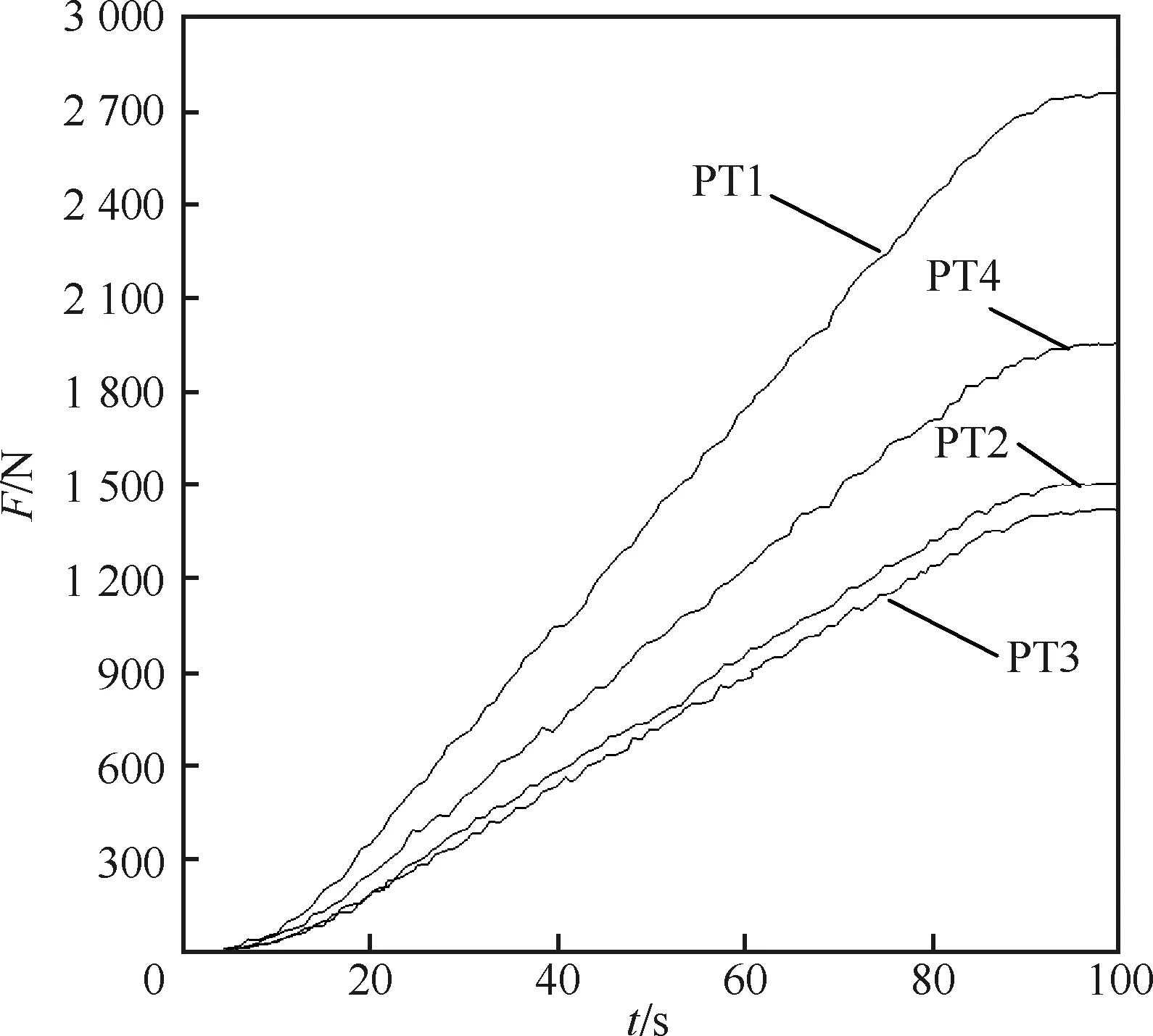
图12 无优选和构造情况下球窝内力随时间的变化曲线Fig.12 Curves for internal force of socket changing with time of no optimization and construction

4个球窝所受铅垂分力也随时间的变化而变化，有的增大，有的变小，由于铅垂内力对壁板和调姿定位系统的危害远小于水平分力，故未对该数据进行详细分析。

壁板从初始位姿调整到目标位姿后，采用Leica-AT960激光跟踪仪对壁板上的测量点进行测量，获得测量点相对于飞机坐标系的实测数据。表3所示为目标位姿处测量点的实测坐标与理论坐标的对比分析。从表3可以看出，在测量点无优选和构造情况下，壁板调姿定位后，测量点超差的个数为9个，其中P2、P3和P11在坐标超差，P4、P5、P16、P17在和两个坐标上超差，P18在和两个坐标上超差， P12在3个坐标上均超差，精度合格的测量点只有P1、P6～P10、P13～P15，共9个测量点，占测量点总数的50%。

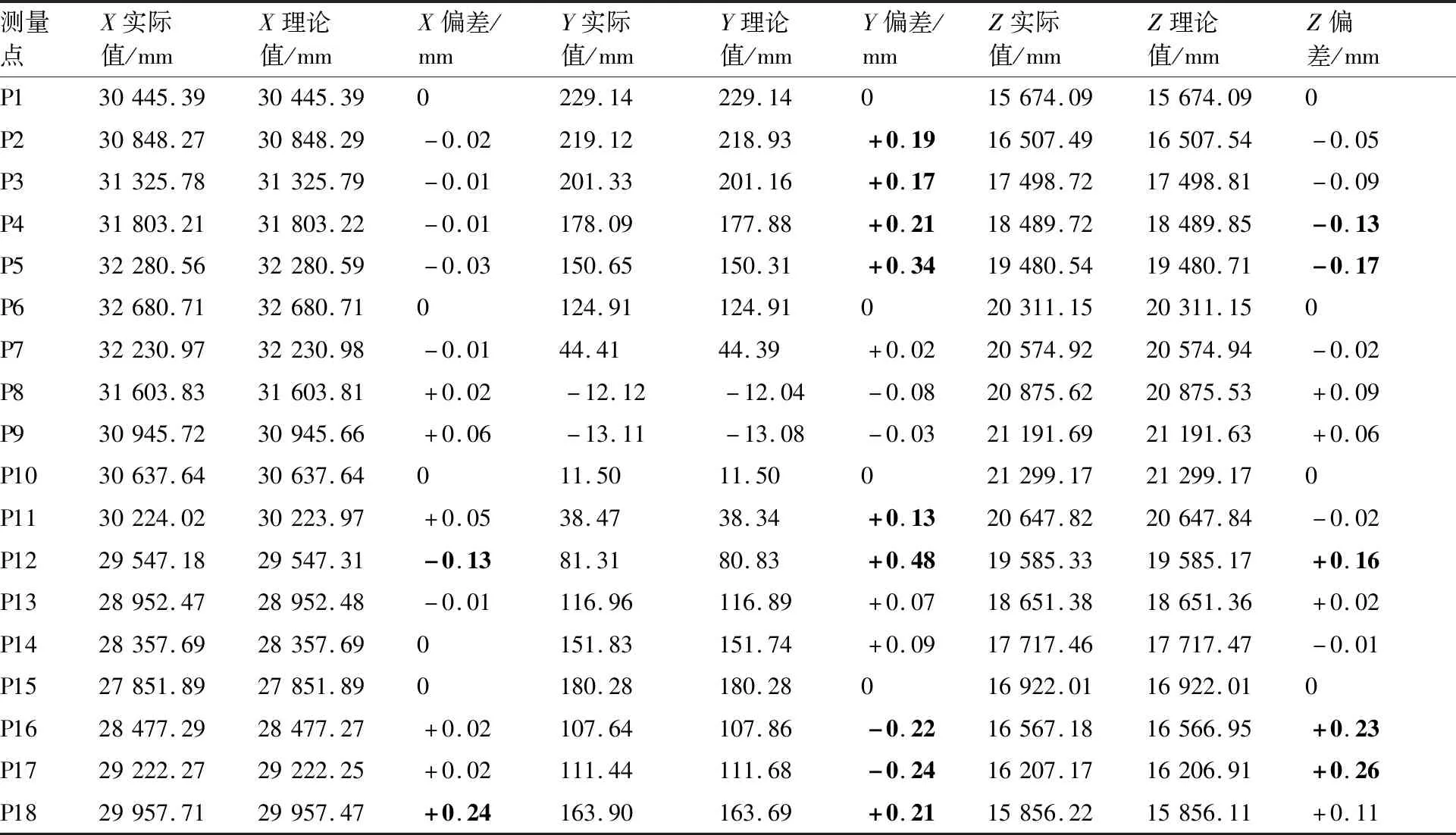
表3 无优选和构造情况下测量点实际坐标与理论坐标的对比分析Table 3 Comparation of actual coordinates of measuring points without optimization and construction with theoretical coordinates

3.2 测量点有优选和构造

将表1数据代入式(1)，将表2数据代入式(2)，计算式(3)～式(5)，将计算结果代入式(6)中进行比较，得出测量点P6、P12、P18不满足有效性判据。将其他15个测量点组成有效测量点，将表1中有效测量点的数据代入式(7)，将表2中有效测量点的数据代入式(8)，构建式(9) 所述的目标函数，对函数进行求解，得

=

=-782503 6,=-185406 0,=975253 6,=0035 2,=0034 2,=0036 6。中的元素和求解所得的6个坐标分量为保留小数点后4位的近似值。

将变换矩阵代入式(21)，获得目标位姿处有效测量点的构造点相对于飞机坐标系的坐标，如表4所示。将式(21)的求解值(表4中的构造值)和式(2)(表2中的坐标值)中的数据代入式(22)，并将式(22)的求解值代入式(23)进行比较，得出所有的有效测量点均满足优选判据。因此，所有的有效测量点就是最终的优选有效测量点(如果在其他试验分析和实际应用中，存在有部分有效测量点不满足优选判据，则按式(24)～式(29) 步骤进一步优选和构造)。

将优选有效测量点(即P1～P5、P7～P11、P13～P17，共15个测量点)的初始坐标数据(表1)和构造坐标数据(表4)分别作为调姿定位系统运动算法中壁板初始位姿和目标位姿时测量点的输入数据，设置调姿定位的时间为100 s，通过运动学算法，得到各个伺服轴的运动学参数与时间的关系。

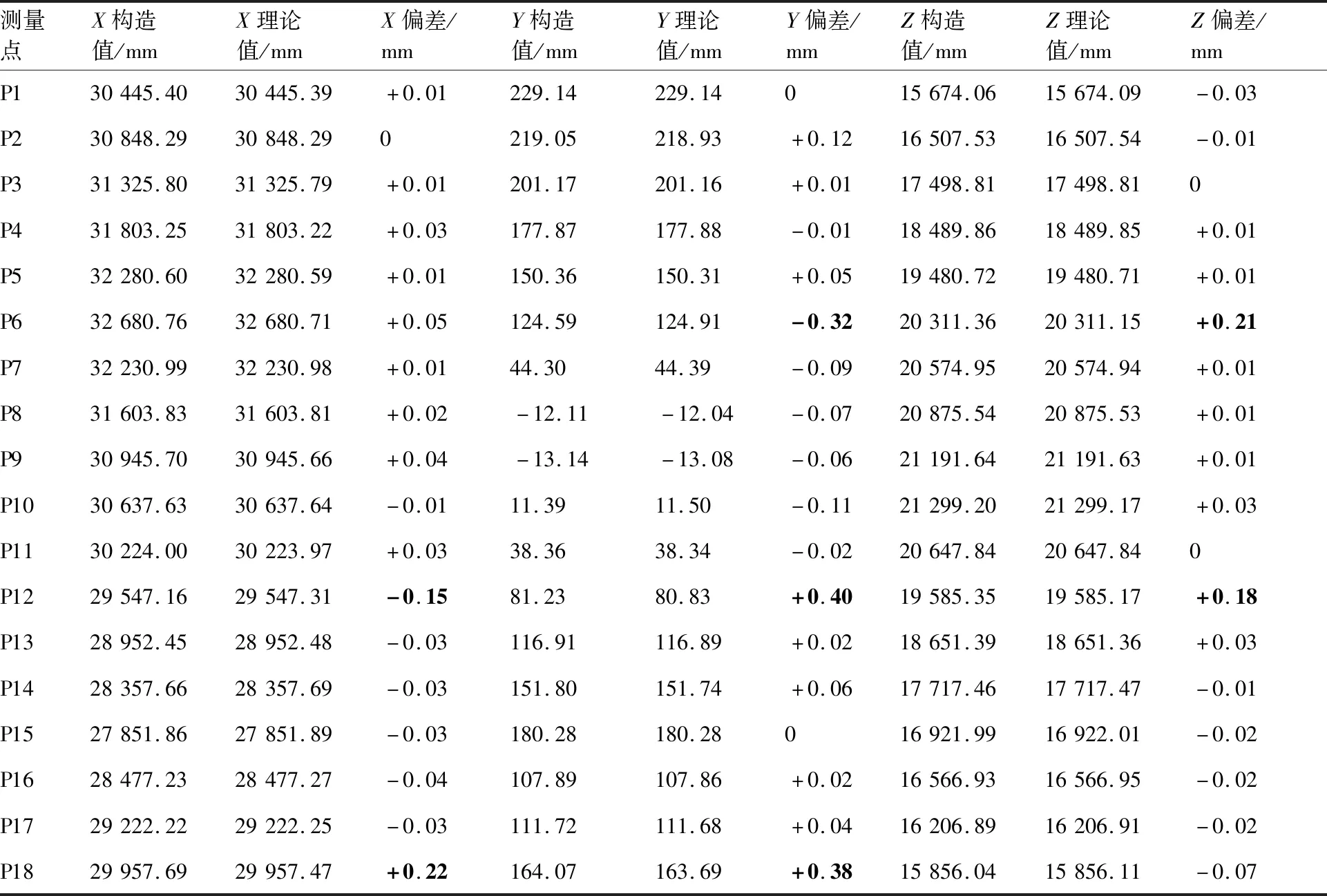
表4 优选和构造情况下测量点构造坐标与理论坐标的对比分析Table 4 Comparison of coordinates for measuring points optimized and constructed with theoretical coordinates

壁板在调姿定位过程中，通过三分位力传感器，记录4个球窝所受水平分力随时间的变化曲线，如图13所示。从图中可以看出，4台三坐标定位器球窝所受的水平内力随时间虽有变化，但变化幅度很小。PT1三坐标定位器在运动过程中，最大的水平内力为43.6 N。由于固连在壁板上的测量点之间的长度在调姿定位前后保持不变，使得调姿定位系统的球铰机构未对整体工艺托架施加迫使变形的作用力，因此，调姿定位系统的内力很小，所监测到的很小的内力是由于球铰副的滑动摩擦力和系统误差所造成的。

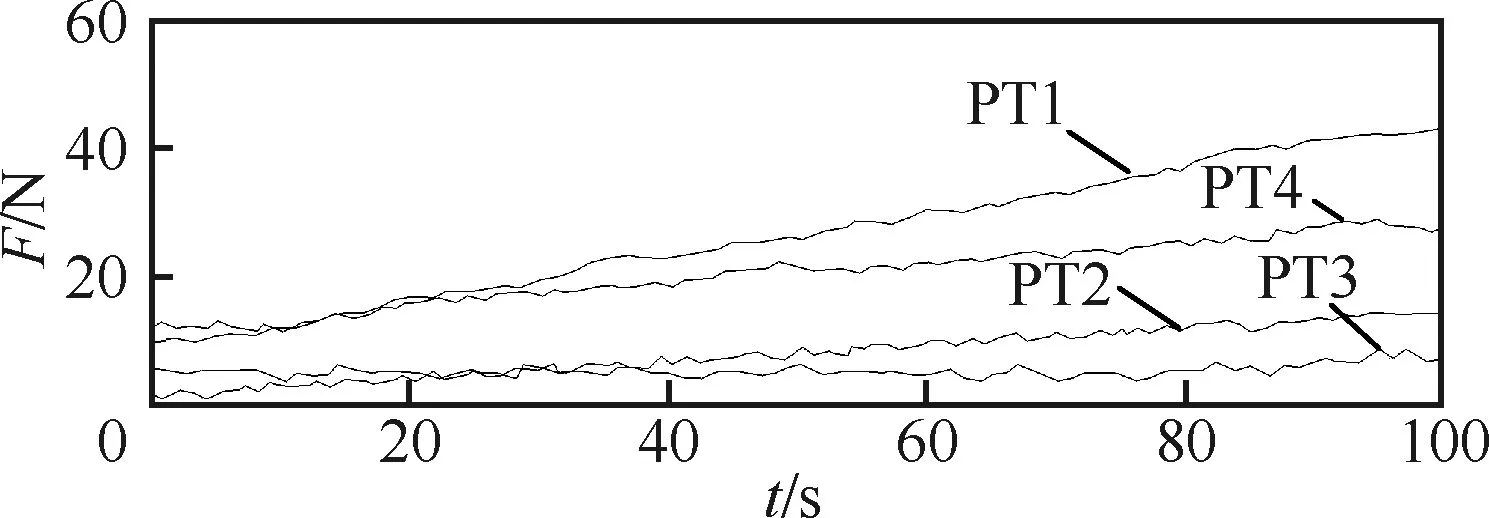
图13 优选和构造情况下球窝内力随时间的变化曲线Fig.13 Curves for internal force of socket changing with time of optimization and construction

壁板从初始位姿调整到目标位姿后，采用Leica-AT960激光跟踪仪对壁板上的测量点进行测量，获得测量点相对于飞机坐标系的实测数据。

表5所示为目标位姿处测量点的实测坐标与理论坐标的对比分析。从表5可以看出，在测量点优选和构造情况下，壁板调姿定位后，测量点超差的个数为3个。依据算法找出的不满足有效性判据的3个测量点为：P6、P12和P18，其他15个测量点均调整到了壁板设计所给定的理论坐标及其公差范围内。

对该壁板进行了多次调姿定位试验分析，记录试验结果如表6所示。结合图12、图13、表3、表4和表5可得如下结论：

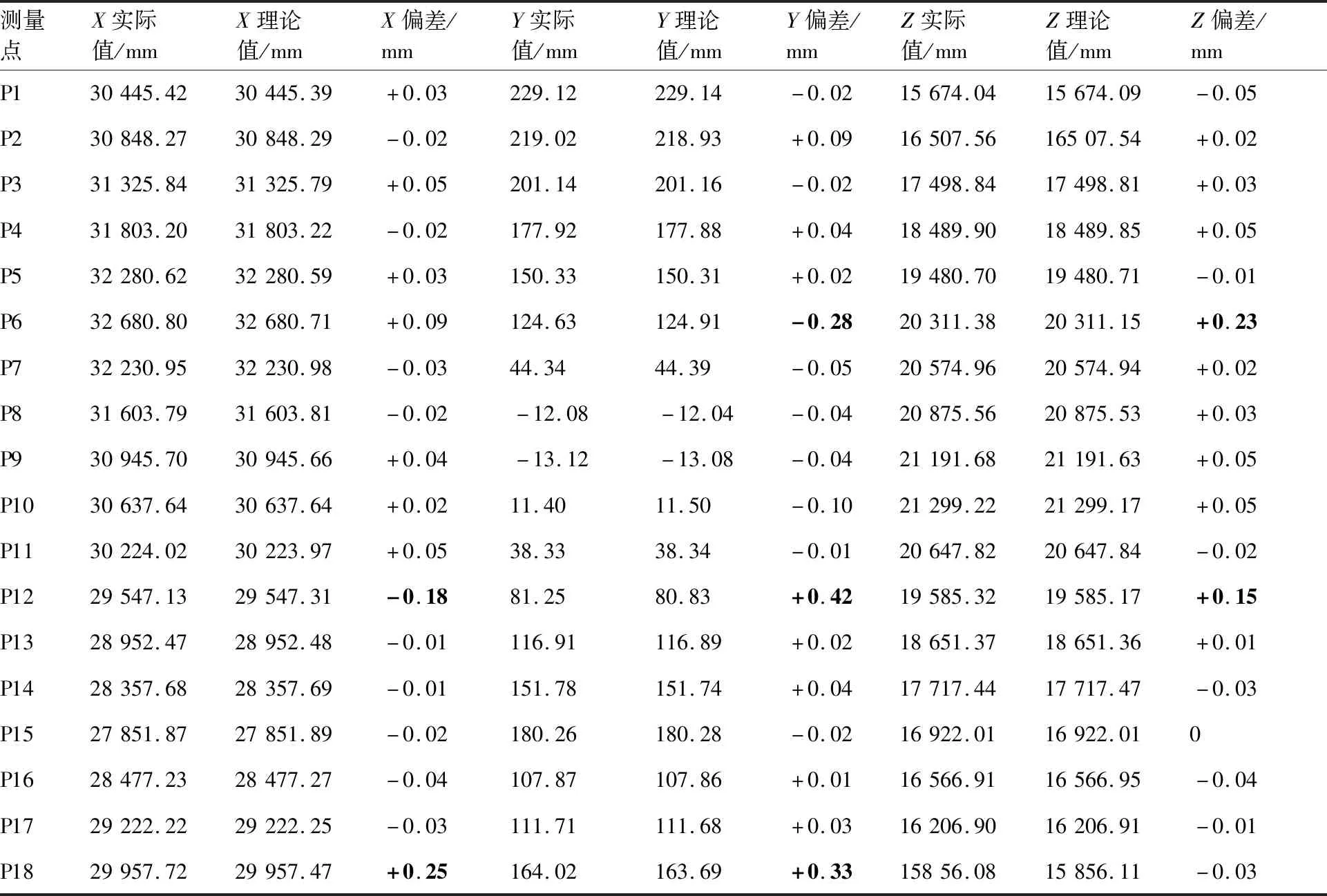
表5 优选和构造情况下测量点实际坐标与理论坐标的对比分析Table 5 Comparation of actural coordinates of measuring points optimized and constructed with theoretical coordinates

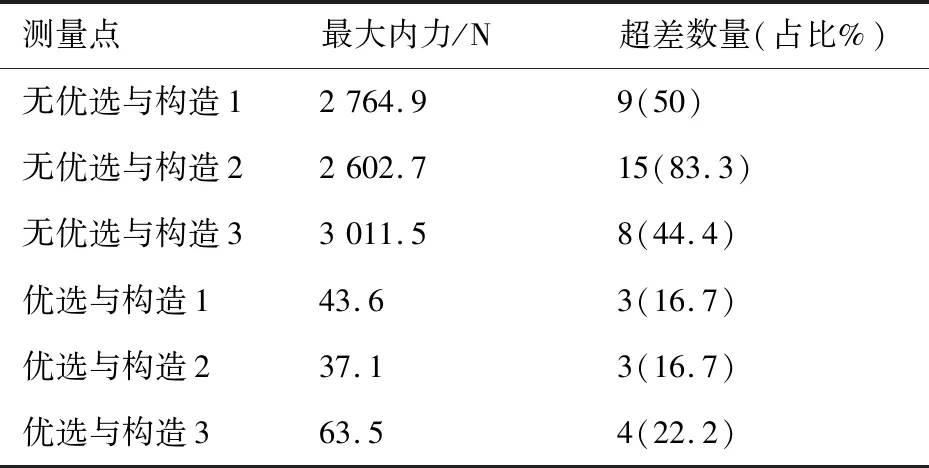
表6 壁板从多个初始位姿调整到目标位姿的结果比对Table 6 Comparison of results obtained by adjusting panels in different initial attitude

1) 在测量点无优选和构造的情况下，将全部测量点初始位姿处的实测坐标和目标位姿处的理论坐标作为调姿定位系统运动算法中壁板初始位姿和目标位姿时测量点的输入数据，由于测量点之间的连线长度在调姿定位前后发生了变化，使得调姿定位过程中系统的内力随时间逐渐增大，水平分力最大值2764.9 N，且约有50%的测量点在调姿定位后存在位置超差，不满足精度要求。

2) 在测量点有优选和构造的情况下，将优选有效测量点初始位姿处的实测坐标和目标位姿处的构造坐标作为调姿定位系统运动算法中壁板初始位姿和目标位姿时测量点的输入数据，由于测量点经优选和构造后，输入到运动算法中的任意两个测量点之间的连线长度在调姿定位前后没有变化，使得调姿定位过程中系统的水平分力变化幅度较小，最大值43.6 N，只有16.7%的测量点在调姿定位后存在位置超差。

4 结 论

固连在飞机部件上的测量点是飞机部件调姿定位的基准和精度检测的依据。首先建立测量点的优选算法，对测量点进行优选；然后建立优选测量点的构造算法，对优选测量点进行坐标构造；最后以优选测量点的初始坐标和构造坐标作为调姿定位系统运动算法的输入数据。飞机壁板数字化调姿定位的工程应用检验发现，采用测量点优选和构造算法后，调姿定位过程中的系统内力，减少到了无优选和构造时的4.4%，满足精度的测量点的数量提高了30%。已在不同飞机部件数字化调姿定位中得到了应用，取得了良好的应用效果。