基于频率变化率的结构刚度非均匀退化识别*

张家滨， 唐 催， 王 磊， 张建仁

(长沙理工大学土木与建筑学院 长沙，410114)

引 言

结构损伤识别是土木工程领域的研究重点，基于结构动力特性的损伤识别技术更是近年来的研究热点,其具有很多静力检测技术不具有的优点，因而在结构损伤识别中得到广泛应用。现阶段常用的损伤识别指标函数有固有频率、模态振型、振型曲率、柔度矩阵及模态应变能等。在结构动力测试中固有频率因最容易获得并且识别精度高而最早应用于结构损伤识别[1-2]。针对结构局部刚度退化评估， Vestroni等[3]利用结构固有频率来识别结构局部裂纹损伤模型。Fernad 等[4]提出基于裂纹模型的结构局部损伤后的频率近似计算方法。Goldfeld等[5]利用结构固有频率来识别均匀损伤模型并将其简化为集中刚度缺失模型。Perera 等[6]分别以结构动态刚度分布和局部模态刚度识别钢筋混凝土结构的损伤。Gillich等[7]利用功率谱和频率变化计算结构损伤，在一定程度上能够较好地识别损伤。但是，固有频率对损伤位置求解的不确定性，使得难以利用固有频率变化有效定位损伤位置，从而限制了该方法的发展。

由于振型曲率对于损伤的敏感性，基于振型的损伤指标函数得到了快速发展。Pandey等[8]通过研究发现，柔度矩阵的改变量对局部损伤识别比固有频率和振型更加敏感。基于结构柔度矩阵的损伤识别方法对损伤位置较为灵敏，能够利用较少的模态参数准确识别结构损伤位置。姚京川等[9]在柔度矩阵的基础上提出了模态柔度曲率改变率的方法，该方法避免了大型矩阵运算，能明显提高运算速度。郭利等[10]采用模态柔度曲率差对弯管结构进行损伤识别。何育民等[11]利用局部柔度的变化来识别管道裂纹的位置和深度。但基于柔度矩阵的方法受到测试精度和测点数量的限制，很难对损伤程度做出较为准确的判断，只能依据各指标的相对大小粗略判断损伤相对程度，无法准确给出损伤区域刚度退化程度。

笔者针对结构局部刚度退化分布非均匀问题，以受弯梁为背景，提出一种新的结构损伤识别方法。首先，利用结构损伤前后的模态挠度曲率差对结构损伤进行定位，确定损伤区域；其次，从损伤动力模型出发，建立损伤位置参数、损伤程度与固有频率之间的关系，通过频率的改变量对结构的损伤程度进行定量分析。数值算例分析表明，该方法对结构损伤识别具有有效性和优越性。

1 结构刚度退化模型

工程结构在野外长期服役，锈蚀、损伤等问题日益突出，极易出现局部刚度退化。针对局部损伤梁结构，以欧拉-伯努利均匀梁模型[12]为基础，如图1所示，假定该梁存在一个均匀损伤区域LD，其区域刚度为EID，其余为未损伤区域且刚度为EIU。定义损伤位置及程度参数如下

(1)

其中：L为梁的长度；LD为损伤区域长度；X为损伤区域起始点坐标；x和b分别为损伤区域的相对起始位置和相对长度；β为损伤程度。

图1 刚度均匀退化模型Fig.1 Degradation model of uniform stiffness

欧拉-伯努利均匀梁自由弯曲振动微分方程为

(2)

其中：ρ为密度；A为截面积。

式(2)的解可表示为v(x,t)=V(x)cos(ωt-φ)，将其代入式(2)可得

(3)

其中：ω为固有频率。

梁模型可以看作3个独立的部分，每个独立的部分均满足如下方程

(4)

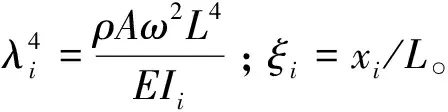
式(4)的解可以写为

Vi(ξi)=Ai1sinhλiξi+Ai2coshλiξi+

Ai3sinλiξi+Ai4cosλiξi

(5)

其中：Aij为任意常数。

引入简支梁边界条件和变形协调条件，并代入式(5)，经过一定的简化处理可得出如下表达式

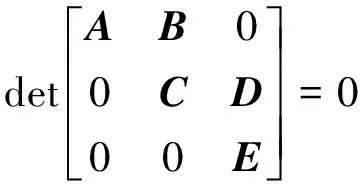
(6)

其中

式(6)建立了参数x，b，β与特征值λ之间的关系

f(λ,x,b,β)=0

(7)

特征方程(7)表明损伤梁的振动频率特征值λD与损伤参数x，b，β存在着对应关系。当损伤前后梁的频率、位置参数x和b已知时，通过式(7)即可求得损伤程度参数β。式(7)是基于结构局部损伤为均匀损伤所得到的损伤程度与频率之间的关系。然而在实际工程中，由于结构受力模式以及环境因素等不同，损伤区域内的刚度退化往往会存在明显的差异，用上述模型来识别结构损伤会对实际工程结构真实状况的评估带来较大的误差，不利于结构后期的维修加固。因此，笔者将结构损伤区域划分成若干节段，将结构损伤区域细化。新建局部刚度非均匀退化识别模型如图2所示。

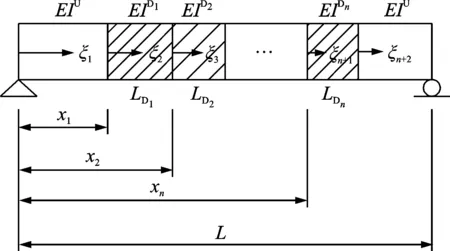
图2 局部刚度非均匀退化模型Fig.2 Heterogeneous degradation model of local stiffness

随着未知刚度区域数量的增加，式(7)虽然适用于多区域模型，振动频率特征值λD与损伤参数xi，bi，βi依然存在着对应关系，但是式(7)将变得十分复杂，且单独利用频率值变化无法同时求解损伤位置和程度。因此，引入模态挠度曲率法先对损伤区域进行定位，然后推导新的关系表达式，建立频率特征值与损伤参数之间的关系，完成损伤程度的识别。

2 模态挠度曲率差指标函数

基于柔度矩阵的结构损伤识别方法无论是结构出现对称损伤、非对称损伤还是损伤位置间距较近以及损伤程度各异的多损伤情况，都能较好地对损伤位置进行定位。因此，由结构柔度矩阵入手，将虚拟外力作用下模态挠度曲率作为损伤指标函数，判断结构损伤位置。

根据林贤坤等[13]提出的模态挠度法理论知,单位静荷载作用下各测点的静位移可以由实测动位移数据求得，单位静荷载作用下各测点的静位移满足

(8)

(9)

对于任意给定的荷载向量，利用柔度矩阵D就可以计算结构各点的挠度，利用模态柔度矩阵Dm可计算各阶模态挠度分量。在损伤区域附近，模态挠度值相对来说有较大的改变，通过对坐标位置二阶导数的作用求模态挠度曲率，变化程度更加明显。基于此，提出模态挠度曲率法(modal deflection curvature，简称MDC)或叠加模态挠度曲率法(superposition of modal deflection curvature，简称SMDC)。设DU，DD分别表示损伤前、后结构柔度矩阵，F为任意节点荷载列向量，则结构挠度为

V=DF

(10)

对挠度进行差分计算挠度曲率

(11)

其中：V(i)为挠度向量的第i个元素值；li为单元长度。

用于计算V的柔度矩阵D可以用模态柔度矩阵Dm替代，形成模态挠度Vm，对应的模态挠度曲率为Wm。

定义模态挠度曲率差(MDC)为

(12)

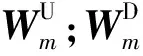
MDC值与单元节点位置坐标相对应，其大小反应了结构损伤前后模态挠度曲率的变化量。当结构局部发生损伤时，局部刚度退化从而引起模态挠度曲率发生变化。如果某一段之间的指标值远大于其他位置处的值或者指标函数曲线发生明显突变，则这个节段之间的单元即为损伤单元。MDC的计算过程可以自由选取各阶模态挠度曲率，也可直接取叠加后的挠度曲率值。

为了说明模态挠度曲率法对结构损伤位置识别的有效性，建立简支梁有限元模型如图3所示，长度为4m，划分为等长的20个单元，每个单元长度为0.2m。其中截面为200mm×350mm的矩形截面，材料弹性模量为32.5GPa，容重为25kN/m3。未损伤梁的前5阶竖向振动固有频率分别为35.10，136.75 ，295.14，496.96和728.27Hz。

图3 简支梁计算模型(单位：mm)Fig.3 Calculation model of simply supported beam (unit: mm)

在实际服役的工程结构中，结构损伤往往使结构刚度发生变化，而对于结构质量的影响几乎可以忽略，因此，可以通过单元刚度的折减来模拟结构损伤。本研究中仅考虑竖向柔度，并取前5阶竖向模态进行仿真识别。考虑到实际结构的损伤一般不会很大，以及损伤因子对结构微损伤的灵敏度，以5号单元刚度缺失程度β分别为2%，5%和10%作为局部均匀损伤的3种工况。选择连续单元4，5，6分别发生不同程度刚度下降作为局部刚度退化分布非均匀的损伤工况，各单元具体损伤程度如表1所示。

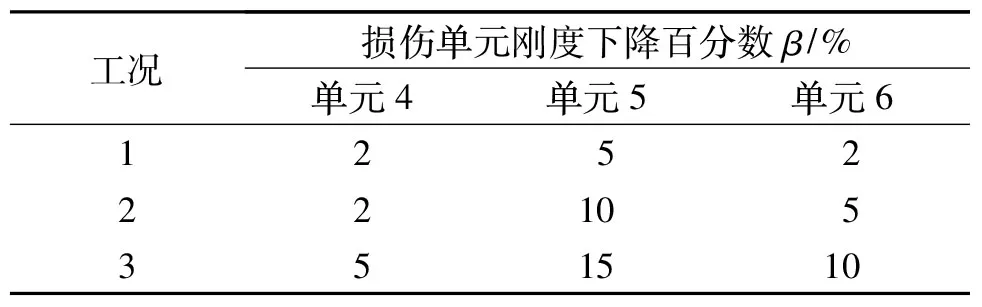
表1 局部刚度非均匀退化工况

采用Matlab编制相应的程序进行计算，结构损伤前后的模态挠度曲率差如图4～图8所示。

图4 第1阶MDC曲线Fig.4 MDC curves of the first mode

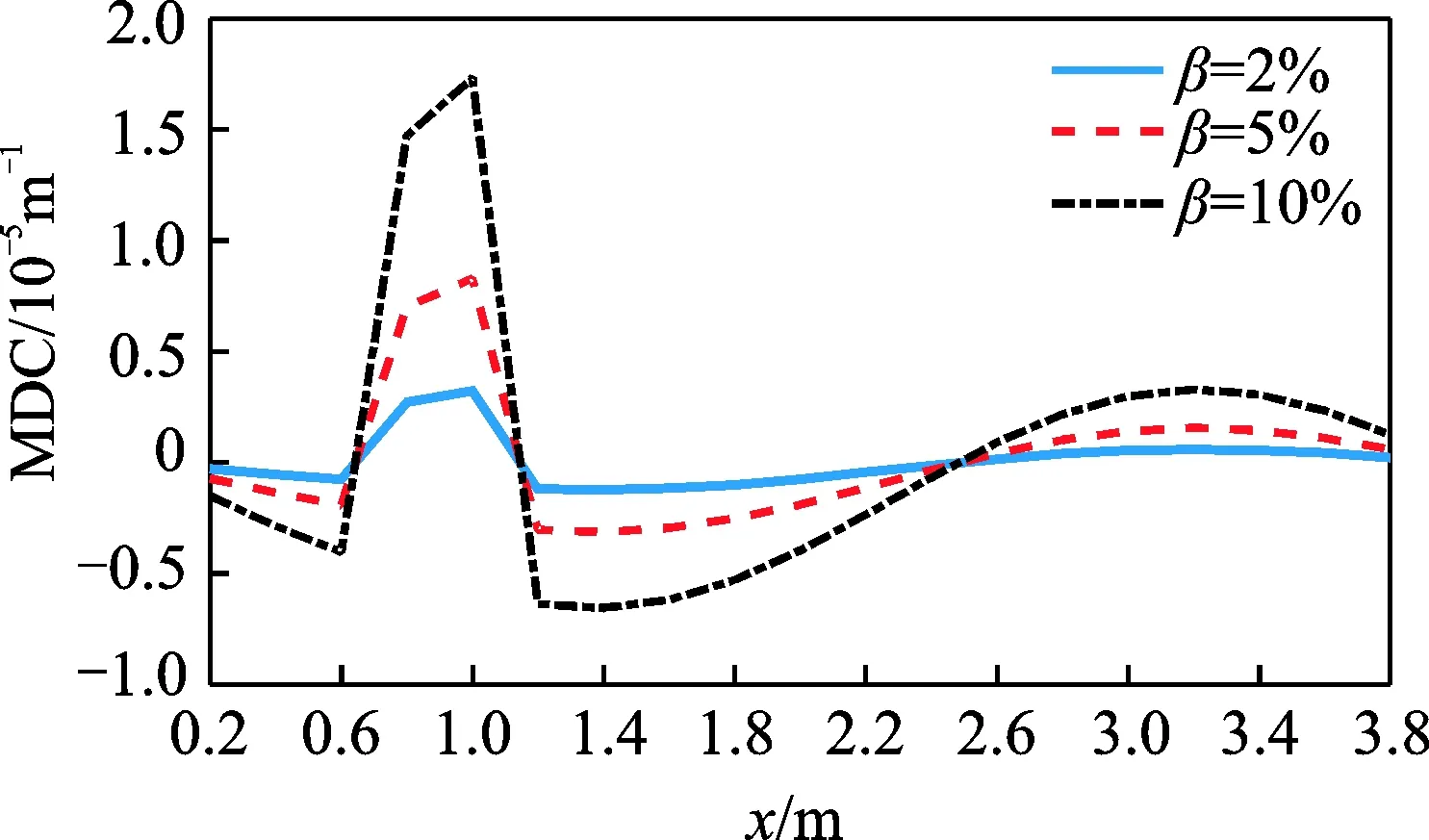
图5 第2阶MDC曲线Fig.5 MDC curves of the second mode

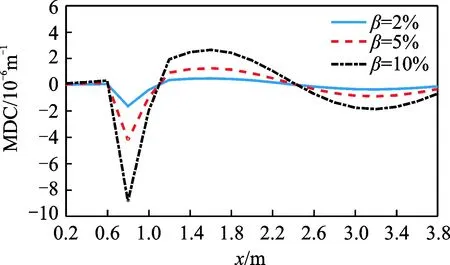
图6 第3阶MDC曲线Fig.6 MDC curves of the third mode

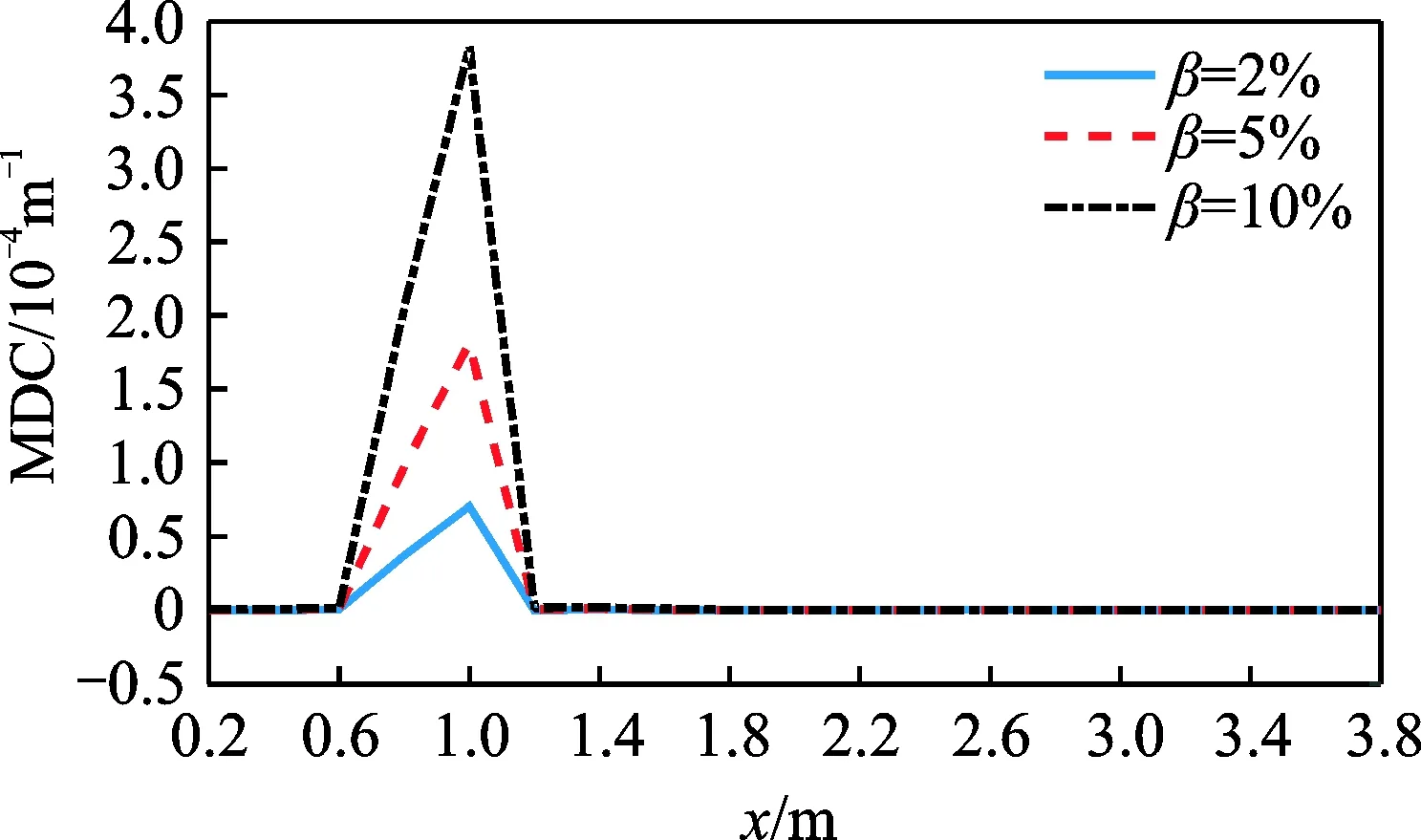
图7 SMDC曲线Fig.7 SMDC curves

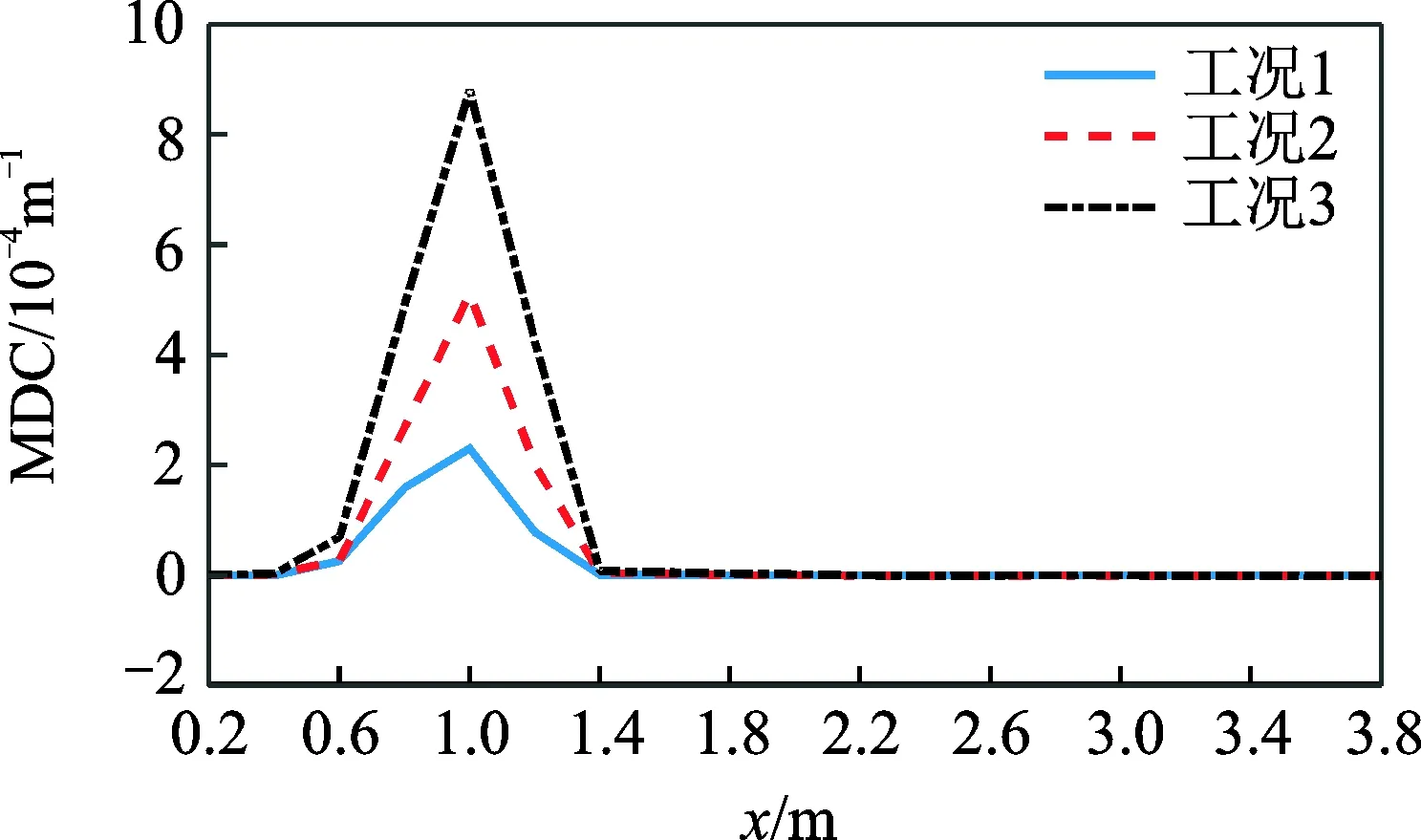
图8 刚度非均匀退化SMDC曲线Fig.8 The SMDC curves of inhomogeneous degenera-ted stiffness

图4～图6分别为局部均匀损伤后前3阶MDC指标函数计算结果，图中横坐标为单元沿长度方向的坐标值，纵坐标为指标值。可以看出，无论损伤程度的大小，损伤后各阶模态挠度曲率都发生了一定的变化，MDC函数曲线产生突变，可根据曲线突变的坐标值准确判断损伤发生的位置。图7为局部均匀损伤前3阶SMDC指标函数的计算结果，在损伤区域内曲线突变明显，而在未损伤区域曲线基本为零直线。相对于单一阶的MDC函数曲线，SMDC函数曲线能够更清晰地指示损伤区域位置。图8为刚度非均匀退化工况的前3阶SMDC指标函数计算结果。同样，在损伤区域内曲线发生明显突变，而未损伤区域其值基本为零，通过图中曲线可以清晰判断出损伤位置与设定位置一致。

在实际工程测试中，可以利用SMDC指标函数识别损伤位置，抗干扰能力更强。然而，无论是均匀损伤还是非均匀损伤，该指标函数值只能表示节点处的模态挠度曲率的改变量，很难准确给出各个区域的刚度变化量，所以将MDC或者SMDC指标函数作为刚度退化识别的第1步，第2阶段利用固有频率对刚度变化的敏感性，通过频率的变化识别结构的损伤程度。

3 基于频率改变率识别刚度退化

局部刚度退化分布识别模型如图2所示。同样考虑均匀欧拉-伯努利梁，将损伤区域划分为n节段，共n+2节段。定义相关参数如下

(13)

其中:各参数意义与式(1)一致。

损伤梁的第i节段的振动模态函数可以用克雷洛夫函数[14]表示

W(ξi)=Ci1Aλiξi+Ci2Bλiξi+Ci3Cλiξi+Ci4Dλiξi

(14)

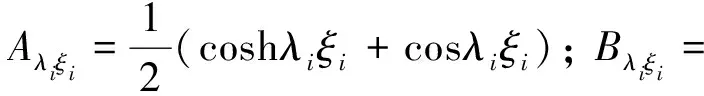
故有

W′(ξi)=λi(Ci1Dλiξi+Ci2Aλiξi+Ci3Bλiξi+Ci4Cλiξi)

(15)

(16)

(17)

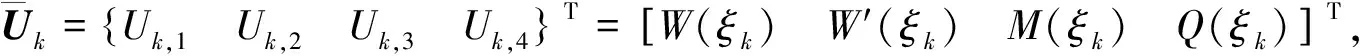
(18)

将式(18)代入(14)可得

(19)

(20)

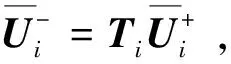
(21)

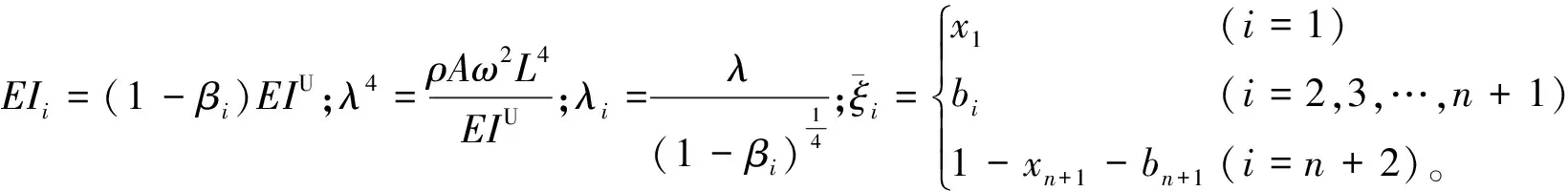
(22)

可得

故

(23)

令

(24)

考虑简支梁边界条件

Wξ1(0)=0，Mξ1(0)=0

可得

即

f(λi,xi,bi,βi)=Z12Z34-Z14Z32=0

(25)

同样，以面局部刚度退化分布非均匀的工况2为例来说明函数关系式(25)的有效性。损伤后梁的前5阶固有频率值分别为34.95，135.58，293.50，496.17和725.86Hz。针对该局部刚度非均匀退化工况，其损伤区域在0.6～1.2m之间。细化识别损伤区域的刚度分布，依次将损伤区域均匀划分为1个节段、2个节段和3个节段，对比分析不同假定工况下刚度退化识别结果，分析算法的有效性。将相应的损伤区域相对位置参数代入式(25)，用Matlab编制相应的程序进行计算。

当将损伤区域视为1段时，相当于均匀损伤模型，在这种情况下，只需要采用任意一阶固有频率值就可以计算该区域的损伤程度。以不同的固有频率值计算，可以对比分析识别结果的有效性和准确性，其结果如图9所示。

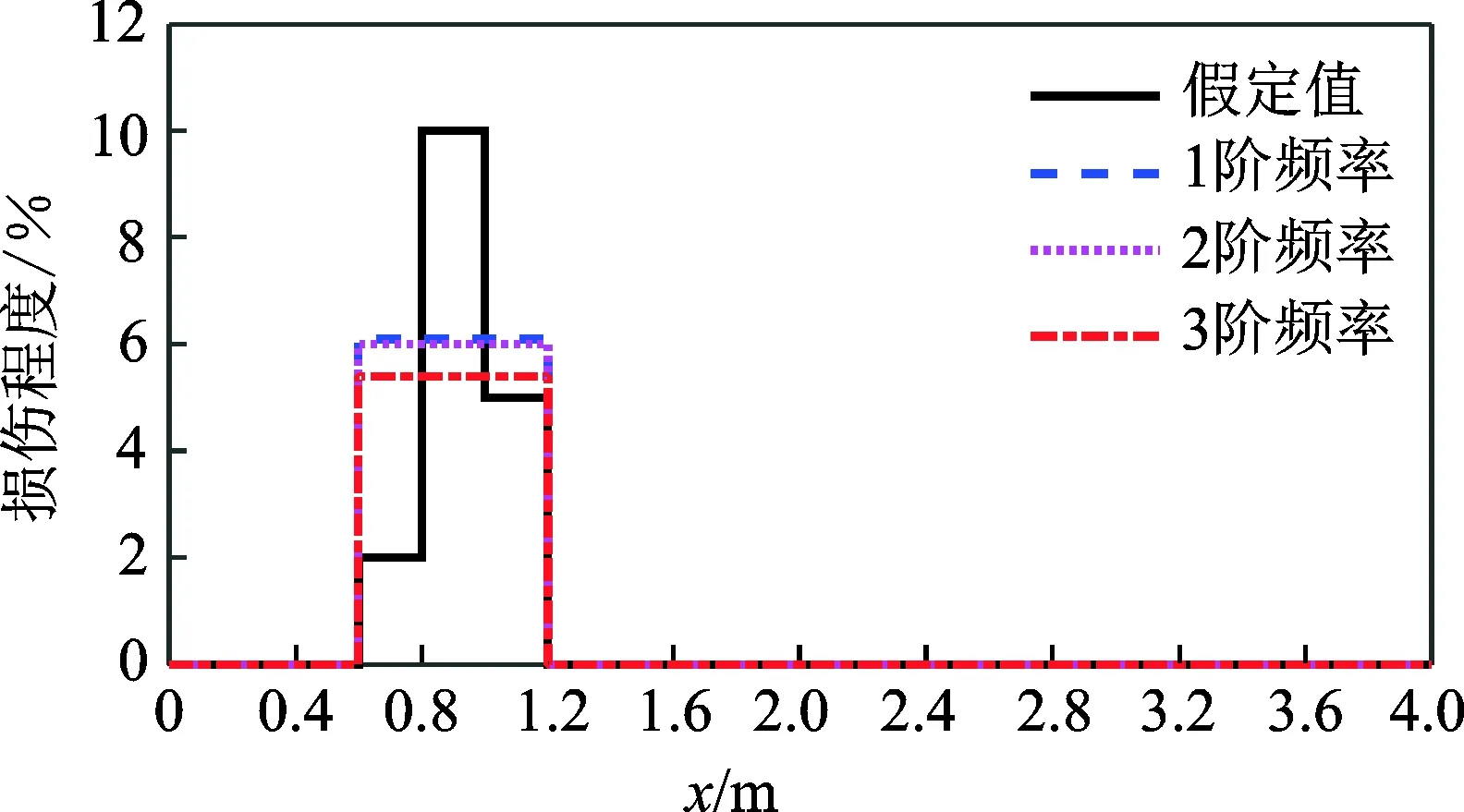
图9 1段识别结果Fig.9 One recognition result

图9表明，采用不同频率计算的结果与假定的不均匀损伤均存在较大的差异，在损伤程度严重的地方识别结果偏小，反之结果偏大，说明以均匀损伤模型来代替非均匀损伤模型不利于结构局部刚度退化的评估。

将损伤区域划分为均匀2段，基于任意2阶固有频率组合的损伤识别结果如图10所示。

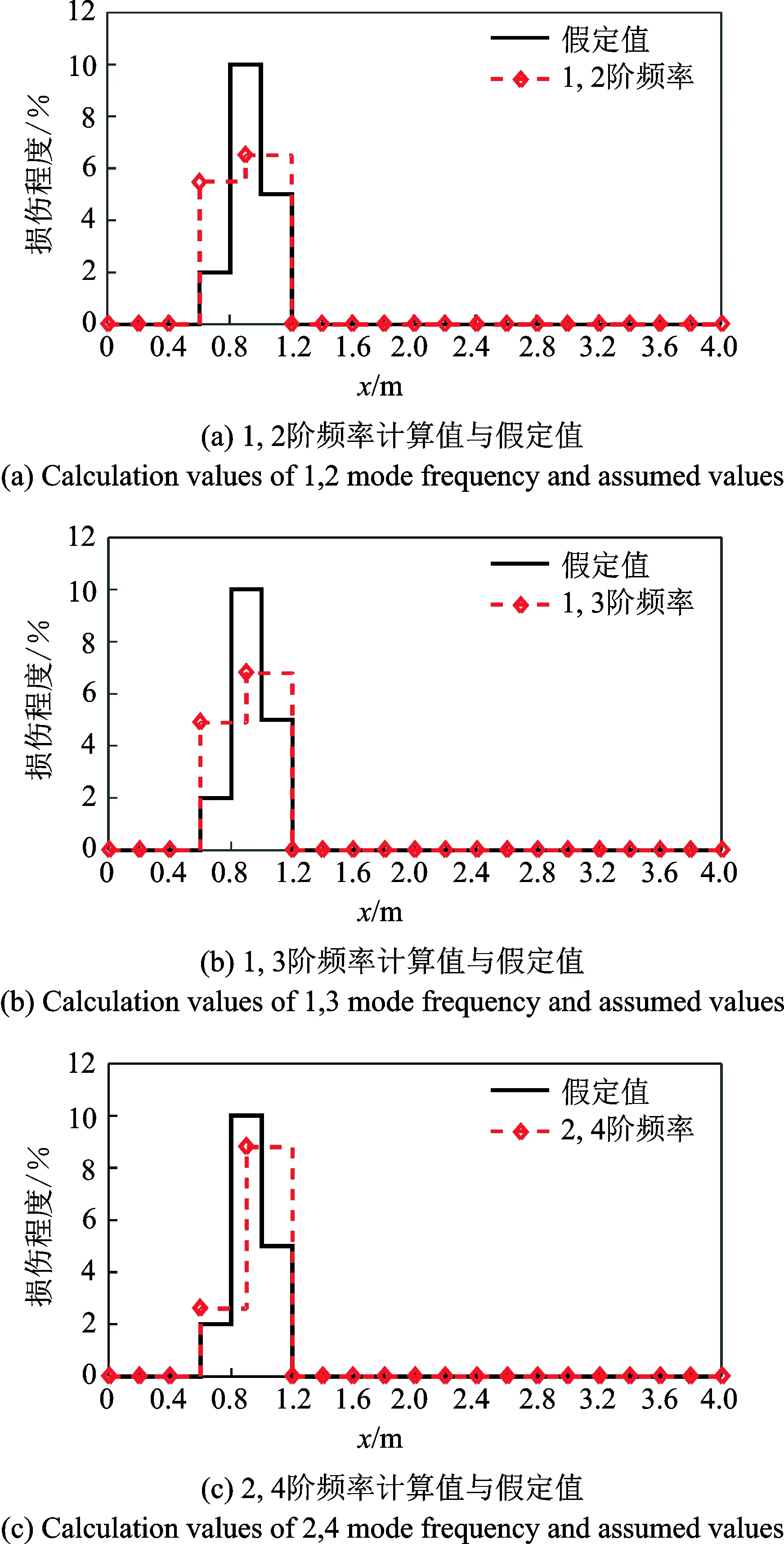
图10 均分2段识别结果Fig.10 Two recognition results

图10为损伤区域分为相等的2段识别结果与假定值对比，其中(a)，(b)，(c)分别表示采用不同频率组合计算结果与假定值的对比情况。从图中分析可知，采用不同频率组合所计算的结果因敏感性的不同而存在一定的差异，且均与假定值存在较大的区别。但是，通过对比分析图9和图10可知，相对于均匀损伤来说，均分两段的识别结果与假定值更为接近，损伤程度识别的结果精度相对较高，误差更小。

当损伤区域均分为3段时，需采用3阶固有频率值进行计算，不同频率组合计算的各区段损伤程度结果与假定值的对比情况如图11所示。

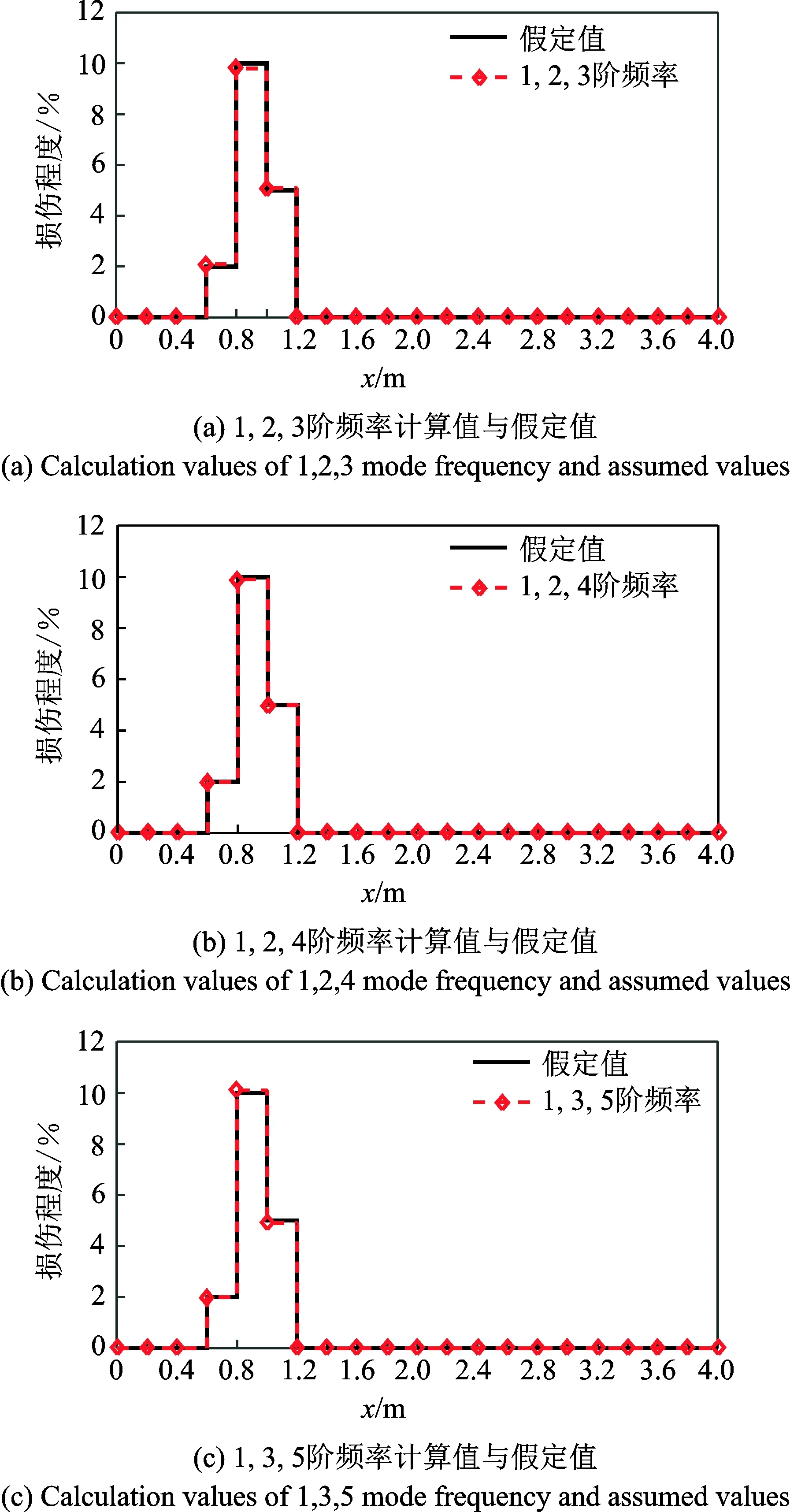
图11 均分3段识别结果Fig.11 Three recognition results

由图11可以看出，损伤区域划分的节段数与假定的损伤分布情况基本符合时，采用任意3阶固有频率组合计算的结果与假定值基本吻合。

通过以上分析可知，随着对损伤区域逐级细化，区域的损伤程度识别精度不断提高。当损伤区域划分与结构实际区域损伤分布接近时，识别的结果与实际的损伤情况基本一致。在损伤程度的识别过程中，随着损伤区域划分节段的增加，需要更多的方程参与计算，所需固有频率阶次数与未知损伤区域节段数量相同。

4 结 论

1) 针对结构局部刚度非均匀退化的损伤模型，通过模态挠度曲率差识别结构损伤位置参数，再从梁结构动力方程入手，通过结构损伤前后的频率特征值变化来计算区域损伤程度。

2) 其中结构任意一阶的MDC指标函数均能有效识别损伤位置，采用不同阶次的MDC指标函数识别结果相互校核，可以避免试验过程中测试误差带来的影响。同时采用SMDC指标函数能有效提高损伤位置识别精度。

3) 以传递矩阵函数建立的固有频率与损伤位置参数、损伤程度之间的关系表达式能够较为准确地计算损伤区域内各节段的损伤程度。通过将损伤区域分节段细化处理，可以提高区域非均匀损伤的识别精度。不足之处在于当未知区域数量增加时所需模态阶次随之增加，对现场的测试结果要求较高。

4) 所提出的方法对于结构局部刚度非均匀退化识别具有明显的优势，同时利用振型和固有频率有效定位刚度退化区域，获取区域内刚度退化分布，对于后续的结构维修加固设计具有很好的指导作用，工程价值显著。

参 考 文 献

[1] Maalej M, Chhoa C Y, Quek S T. Effect of cracking, corrosion and repair on the frequency response of RC beams [J]. Construction and Building Materials,2010,24:719-731.

[2] Capozucca R. A reflection on the application of vibration tests for the assessment of cracking in PRC/RC beams [J]. Engineering Structures,2013,48: 508-518.

[3] Vestroni F, Capecchi D. Damage detection in beam structures based on frequency measurements [J]. Journal of Engineering Mechanics,2000,126(7):761-768.

[4] Fernad N S E J, Rubio L, Navarro C. Approximate calculation of the fundamental frequency for bending vibrations of cracked beams [J]. Journal of Sound and Vibration,1999, 225(2):345-352.

[5] Goldfeld Y , Elias D. Using the exact element method and modal frequency changes to identify distributed damage in beams [J]. Engineering Structures,2013,51(2):60-72.

[6] Perera R, Huerta C, Juan M O. Identification of damage in RC beams using indexes based on local modal stiffness [J]. Construction and Building Materials,2008,22:1656-1667.

[7] Gillich G R, Praisach Z I. Modal identification and damage detection in beam-like structures using the power spectrum and time-frequency analysis [J]. Signal Processing,2014, 96:29-44.

[8] Pandey A K, Biswas M. Damage detection in structures using changes flexibility [J]. Journal of Sound and Vibration,1994,169(1):3-17.

[9] 姚京川,杨宜谦,王澜. 基于模态柔度曲率改变率的桥梁结构损伤识别方法[J]. 中国铁道科学,2008(5):51-57.

Yao Jingchuan, Yang Yiqian, Wang Lan. Damage detection method for bridge structure based the modal flexibility curvature change ratio [J]. China Railway Science, 2008(5):51-57.(in Chinese)

[10] 郭利,张瑞刚,李永军,等. 基于模态柔度曲率差的弯管结构损伤识别[J]. 振动、测试与诊断,2013,33(5):902-906.

Guo Li, Zhang Ruigang, Li Yongjun, et al. Damage identification of bend-type structure based on modal flexibility-curvature and difference [J]. Journal of Vibration, Measurement & Diagnosis,2013,33(5):902-906.(in Chinese)

[11] 何育民,高攀,张小龙,等. 局部柔度变化在管道裂纹定量识别中的应用[J]. 振动、测试与诊断,2015,35(6):1184-1189.

He Yumin, Gao Pan, Zhang Xiaolong, et al. Pipe crack quantitative identification based on the change of the local flexibility [J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(6):1184-1189 .(in Chinese)

[12] Cerri M N, Vestroni F. Detection of damage in beams subjected to diffused cracking [J]. Journal of Sound and Vibration,1999,2887: 259-276.

[13] 林贤坤,张令弥,郭勤涛,等. 基于模态挠度法的预应力连续箱梁桥状态评估[J]. 土木工程学报,2010,10:83-90.

Lin Xiankun, Zhang Lingmi, Guo Qintao ,et al. Application of modal deflection method for condition assessment of prestressed concrete continuous box-girder bridges [J]. China Civil Engineering Journal,2010,10:83-90.(in Chinese)

[14] Zhang Xiaoqing, Ph D, Han Qiang, et al. Analytical approach for detection of multiple cracks in a beam [J]. Journal of Engineering Mechanics,2010,136(3):345-357.