伸展运动悬臂梁振动特性及能量分析*

刘 明, 杨晓东, 张 伟， 秦朝红

(1．北京理工大学先进结构技术研究院 北京，100081) (2．北京工业大学机械结构非线性振动与强度北京市重点实验室 北京，100124) (3．北京强度环境研究所可靠性与环境工程技术重点实验室 北京，100076)

引 言

在科学技术和工程中经常遇到一类振动体系，其动力学参数随时间变化，此类系统称为时变参数系统。轴向可外伸悬臂结构在工程中有较多的应用，比如航天器外伸天线的展出、可伸缩机翼的伸出等，都属于时变参数结构。这类时变结构因其沿轴向是可运动的，因此为非保守系统，相比于不可移动的结构，其沿轴向外伸过程更易诱发结构的横向振动。

轴向运动连续体本身属于无穷维陀螺连续系统，陀螺项的存在对振动的分析提出很重要的理论要求，而做伸展运动的连续体的横向振动微分方程及其边界条件都属于时变系统，这给问题的求解带来诸多技术问题。时变参数系统的振动要比恒定参数体系的振动复杂的多。恒定参数连续体在初始时刻处在它的某个振型，不受外力作用，它就会永远处在这个振型中；但一个变参数体系，即使不受外力作用，也会发生不同振型间的跳跃。

对于伸展运动悬臂梁结构，如升降机[1]、带锯[2]等，许多学者已经做出了一些初步的研究。Tabarrok等[3]推导了长度随时间变化梁的振动方程，其表现形式为4个非线性偏微分运动方程和一个几何关系的运动方程，最后通过一些假设，将这些方程转化为线性时变参数方程，并求得了匀速运动时的解析解。Zhu等[4]研究了一系列任意变长度梁的线性动力学问题，得出了为了保持梁的稳定性，不仅要抑制梁的振动能量，还要缩短梁的长度和振幅响应的结论。因为对于时变参数系统，位移的有界性并不能保证振动能量的有界性，Gosselin等[5]研究了稠密液体中外伸梁的稳定性，用黏性力和附加质量代替了流体对梁的影响，然后用牛顿第二定律推导了梁的振动方程，对方程无量纲化之后，采用Galerkin截断研究了梁在伸展过程中的稳定性问题。Pastenak等[6]研究了带有负刚度多自由度弹簧振子系统的稳定性问题，用解析方法推导了根据刚度矩阵的行列式值来判断系统失稳的条件，并以两自由度弹簧振子为例验证了他们的结论。近年来，其他学者针对不同的伸展运动梁模型，也做了相关的理论研究[7-14]和实验研究[15-18]。

有关伸缩悬臂梁结构的时变参数系统的瞬态动力学分析虽然起步较早，但是前期研究的模型较为简单，且没有实验方面的研究。直到近几年，才逐渐出现了实验研究。这些研究主要集中在建立伸展运动梁的振动微分方程，以及分析其伪固有频率、振幅等一些动力学特性。早期的研究集中于低速运动伸展梁的振动特性，而在伸展运动悬臂梁失稳之后横向振动能量的变化趋势研究较少。笔者利用梁横向振动微分方程，分析了伸展梁的振动特性，重点讨论失稳后的能量变化情况。

1 伸展运动悬臂梁模型

伸展运动悬臂梁模型见图1。梁在滑槽内的部分受力F的作用，随着力F方向的改变，该悬臂梁可进行外伸和回收，其长度L是时间的函数，即L=L(t)。

图1 伸展运动悬臂梁模型Fig.1 Stretching cantilever beam model

为了讨论失稳状态，只研究外伸情况。在一定初始条件下，梁在外伸过程中，会产生横向振动。相比于横向振动，轴向的振动很小，故在此对轴向振动不做分析。其中，梁的材料参数[11]见表1。

表1 材料参数

2 研究内容

取梁一微段dx进行受力分析，如图2所示。

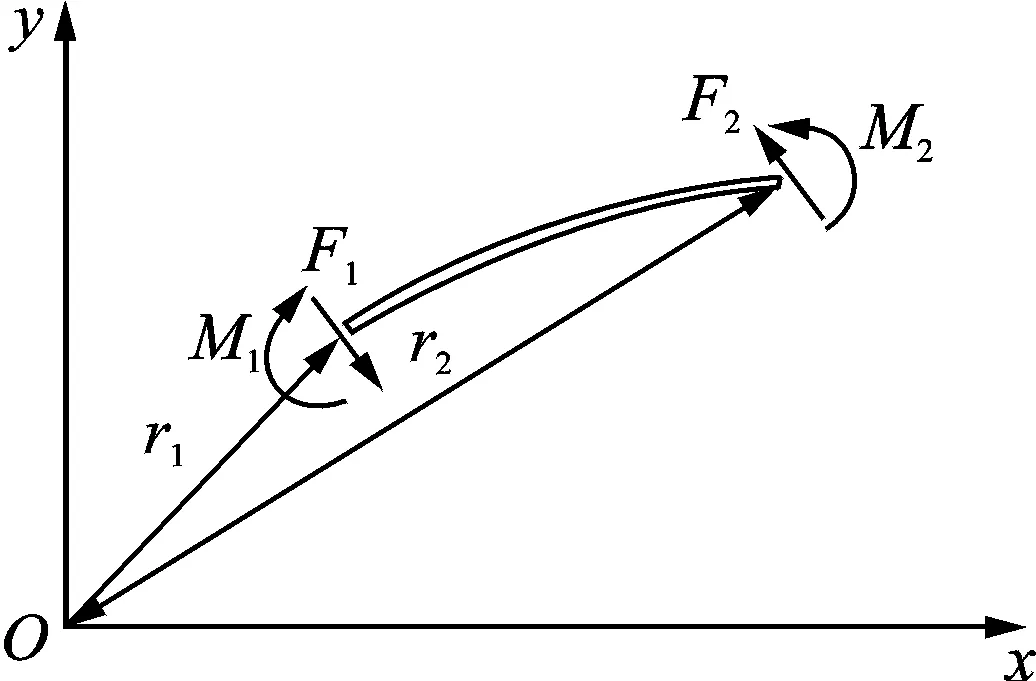
图2 梁微段受力分析Fig.2 End forces on a segment of the beam

对上述微段用动量矩定理和动量定理，得

将式(1)和式(2)经过数学变化，可得

(3)

利用假设模态方法，将式(3)转化为

(4)

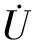
其他各参数如下

(5)

式(5)即为伸展运动悬臂梁横向振动微分方程[3]。

2.1 外伸梁运动状态

当梁轴向伸展速度U=1.3 m/s，加速度a=dU/dt=0时，对式(4)取1阶截断，并令初始条件f1=0.1，df1/dt=0，可得出梁自由端位移响应曲线，如图3所示。

由图3可知，梁在外伸初始阶段，其自由端位移呈周期性逐渐增大，此时处于稳定阶段。当梁伸展到一定程度时，自由端偏向于坐标轴一方一直伸展下去，系统的周期性震荡彻底消失，此时处于屈曲失稳状态。不同于经典的时不变参数结构，目前对于时变参数结构还没有清晰的稳定性定义。笔者所采用的稳定性概念定性为振动失去往复性的情况，即对应于时不变参数结构的屈曲。但时变结构参数失稳的临界点并不是精确的临界值，而是一范围。

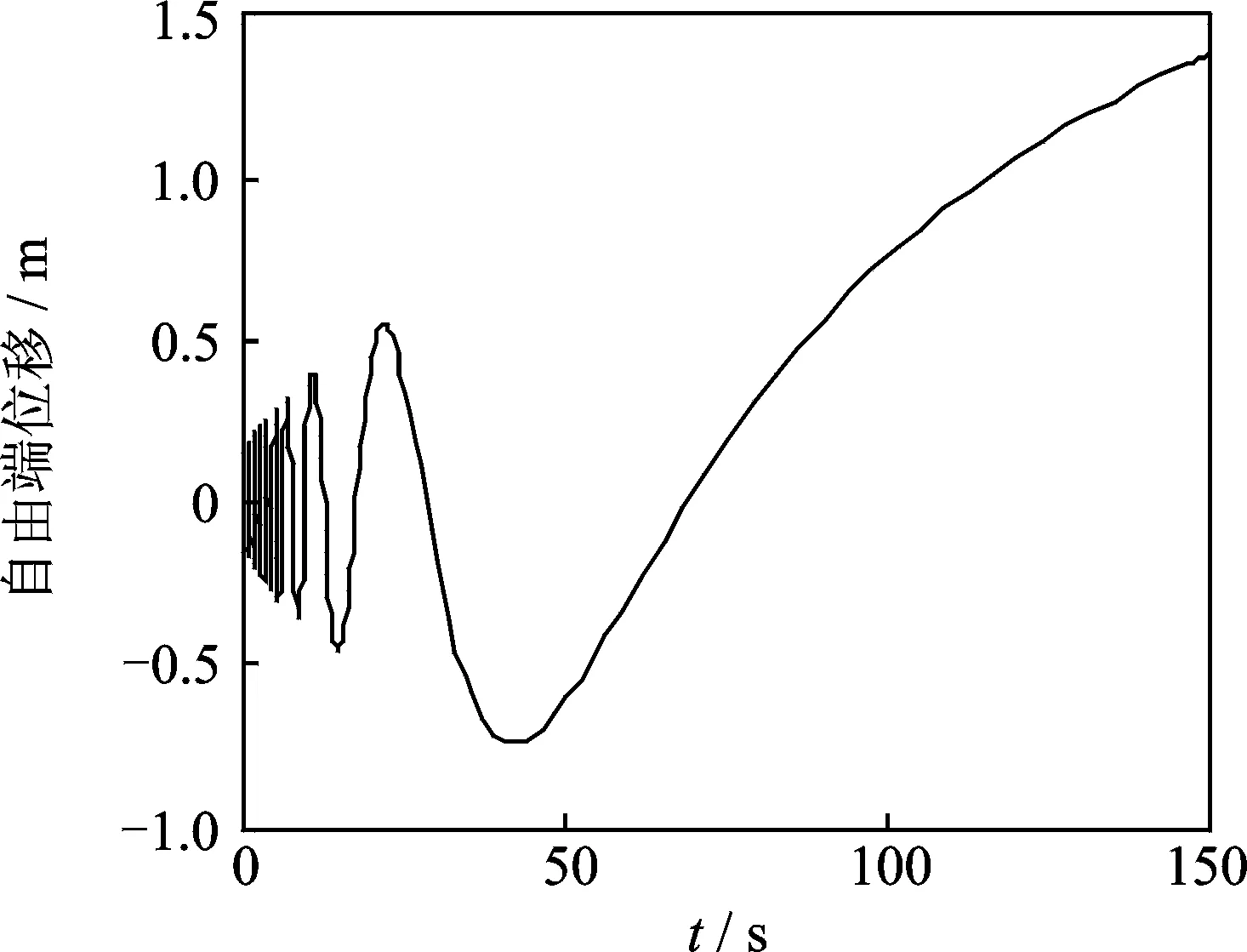
图3 梁自由端位移响应Fig.3 The tip displacement response

2.2 能量变化趋势

以1阶模态位移作为初始条件，即

{0.1 0 0 0 … 0}

(6)

由式(4)可得出梁横向振动的动能Ek、势能Ep和总能量Et表达式为

(7)

基于对式(4)的求解，应用4阶截断的式(7)可以绘出能量随时间的变化。当梁以U=0.8 m/s的速度进行外伸时，其能量由稳定阶段到失稳阶段的变化曲线见图4。图中横坐标为梁伸展时间，纵坐标为能量，黑色点划线代表动能Ek，红色实线代表势能Ep，蓝色虚线代表总能量Et。

图4 能量变化图Fig.4 Energy variation diagram

很明显，梁在外伸过程中可以分为稳定阶段、失稳初期和失稳后期3个阶段。分析图4中曲线，可得以下结论：

1) 稳定阶段，随着梁的外伸，其刚度逐渐变小，质量逐渐增大，振动频率减小，所以动能、势能和总能量逐渐减少；

2) 在梁失稳初期，动能、势能和总能量几乎不变；

3) 在梁失稳后期，动能变大，势能随着负刚度的出现，在反向逐渐变大，总能量的变化很小。

2.3 能量分配趋势

在以1阶模态位移作为初始条件下，梁在失稳之前，能量由低阶模态开始，逐渐向高阶模态分配，且距离初始条件阶数较近的模态获得的能量较多。在梁失稳之后，能量依旧由低阶模态向高阶模态依次分配，随着时间的增长，距离初始条件阶数较远的获得的能量较多。

以1阶模态位移作为初始条件，梁在外伸过程中由稳定阶段到失稳以后的振动挠曲线轮廓如图5所示。

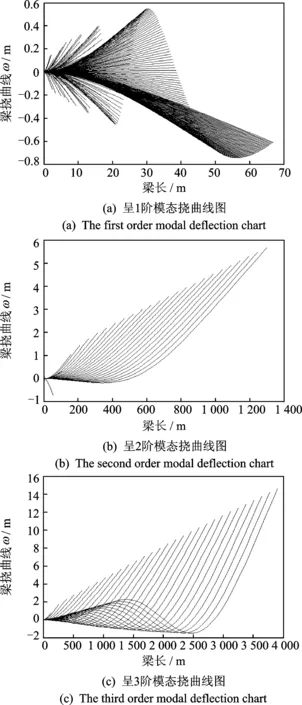
图5 挠曲线轮廓图Fig.5 The contour of the deflections

分析图5可知：

1) 随着时间的推移，梁的往复震荡逐渐减弱，直到失稳之后，往复震荡消失；

2) 失稳之后，梁由1阶模态的伸展变成了2阶模态，随着梁的不断伸长，又变成了更高阶的模态。

用Runge-kutta法求解式(4)可以确定能量在各模态分配的大小，前5阶的振动变化由图6给出。

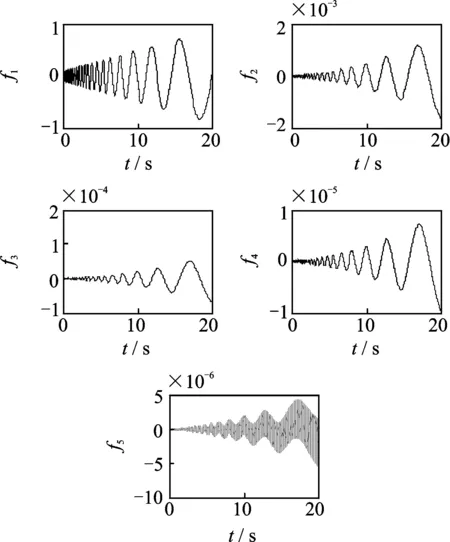
图6 稳定阶段时能量的传递Fig.6 The energy transfer in stable stage

图6中分别画出了前5阶模态所含能量大小的曲线，可得以下结论：

1) 1阶模态位移除了引起第1阶模态振动，还引起了其他模态的振动，这种现象在线性系统里面不会出现；

2) 距离初始条件阶数较近的模态分配到的能量较多，距离较远能量越少；

3)f1的变化与稳定阶段的能量变化趋势相对应，表明振动频率逐渐变小，动能减小，在数值上f1虽逐渐增大，但由于刚度减小的原因，最终致使势能减小。

观察式(4)可知，-(A+B)U2/L2是引起能量在各模态之间分配的因素，其中矩阵A为反对称矩阵，B为对称矩阵，因此-(A+B)U2/L2导致了各模态之间的耦合。

梁失稳后，其能量在各模态之间的分配如图7所示。图7中分别画出了前5阶模态所含能量大小的曲线，由图7可得以下结论：

1) 失稳初期，距离初始条件阶数较近的模态，分配的能量多；

2) 失稳后期，距离初始条件阶数较远的模态分配的能量比较多，甚至超过了初始条件所给予的能量，与前面由1阶模态的伸展，变成高阶模态的伸展相对应；

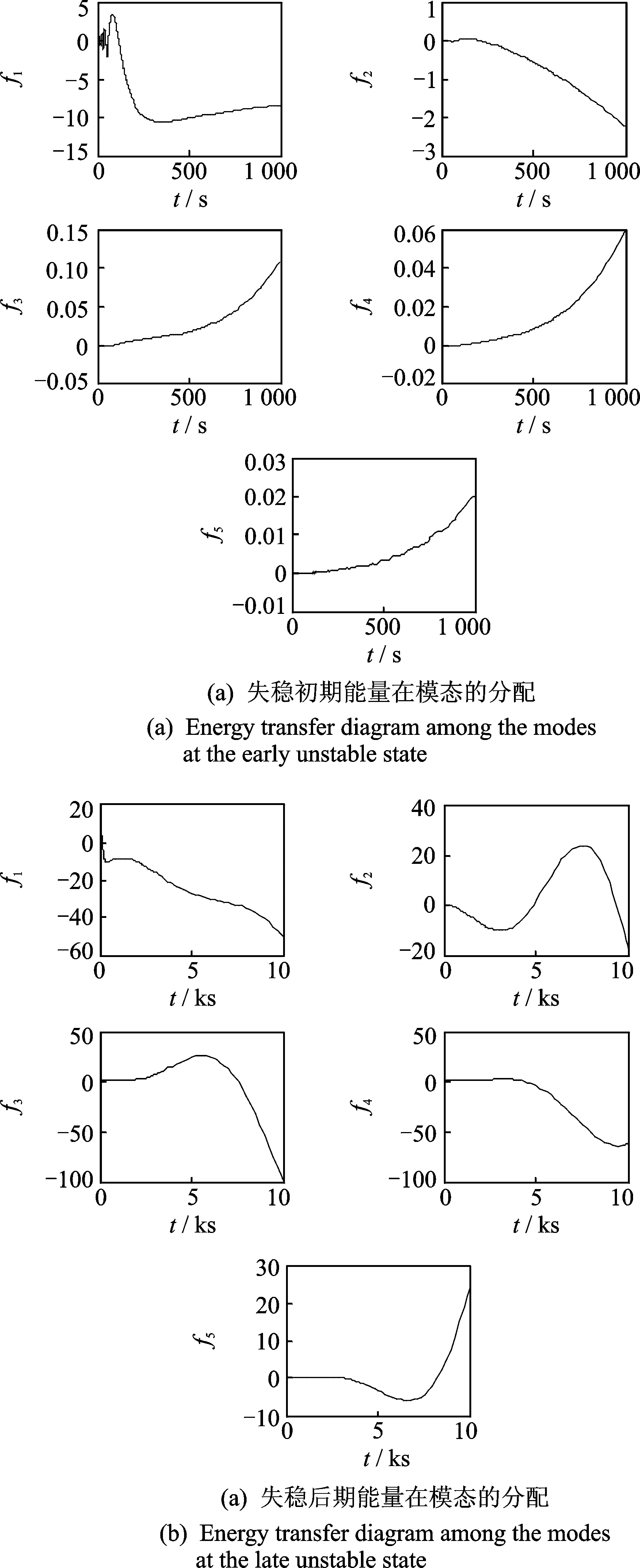
图7 能量在模态的分配Fig.7 Energy transfer diagram among the modes

3) 梁在失稳后期，f1的变化与势能变化相对应，其在数值上大幅度增加，再加上负刚度的影响，导致势能在反向逐渐增大。

3 结束语

笔者利用伸展运动梁的微分方程，分析了梁在失稳前后的能量变化情况，发现随着梁的外伸，动能、势能和总能量逐渐减小。在失稳初期，动能、势能和总能量基本不变;在失稳后期，动能逐渐变大，势能反向变大，总能量变化不大。最后还发现梁在失稳以后，能量在各模态之间分配的规律与失稳前能量分配规律有较大的变化。

参 考 文 献

[1] Terumichi Y, Ohtsuka M, Yoshizawa M, et al. Nonstationary vibrations of a string with time-varying length and a mass-spring system attached at the lower end[J]. Nonlinear Dynamics, 1997,12(1):39-55.

[2] Mote C D. A study of band saw vibrations[J]. Journal of the Franklin Institute, 1965, 279(6): 430-444.

[3] Tabarrok B, Leech C M, Kim Y I. On the dynamics of an axially moving beam[J]. Journal of the Franklin Institute,1974, 297(3):201-220.

[4] Zhu Weidong, Ni J.Energetics and stability of translating media with an arbitrarily varying length[J]. ASME Journal of Vibration Acoustics, 2000, 122(3): 295-304.

[5] Gosselin F, Paidoussis M P, Misra A K. Stability of a deploying/extruding beam in dense fluid[J]. Journal of Sound and Vibration, 2007, 299(1-2): 124-142.

[6] Pasternak E, Dyskin A V, Sevel G. Chains of oscillators with negative stiffness elements[J]. Journal of Sound and Vibration, 2014, 333(24): 6676-6687.

[7] Zhu Kefei, Chung J T. Nonlinear lateral vibrations of a deploying Euler-Bernoulli beam with a spinning motion[J]. International Journal of Mechanical Sciences, 2015, 90:200-212.

[8] Wang Lihua, Hu Zhendong, Zhong Zheng, et al. Dynamic analysis of an axially translating viscoelastic beam with an arbitrarily varying length[J]. Acta Mechanica,2010,214(3): 225-244.

[9] Wang Lin, Ni Qiao. Vibration and stability of an axially moving beam immersed in fluid[J]. International Journal of Solids and Structures, 2008, 45(5): 1445-1457.

[10] Park S, Yoo H H, Chung J. Eulerian and lagrangian descriptions for the vibration analysis of a deploying beam[J]. Journal of Mechanical Science & Technology, 2013, 27(9):2637-2643.

[11] Misra A K, Kalaycioglu S. Approximate solutions for vibrations of deploying appendages[J]. Journal of Guidance Control & Dynamics, 2012, 14(2):287-293.

[12] Ghayesh M H, Amabili M. Nonlinear vibrations and stability of an axially moving Timoshenko beam with an intermediate spring support[J]. Mechanism & Machine Theory, 2013, 67:1-16.

[13] Chang J R, Lin W J, Huang C J,et al. Vibration and stability of an axially moving rayleigh beam[J]. Applied Mathematical Modelling, 2010, 34(6):1482-1497.

[14] Cooper J. Asymptotic behavior for the vibrating string with a moving boundary[J]. Journal of Mathematical Analysis and Applications, 1993, 174(1): 67-87.

[15] Duan Yingchang, Wang Jianping, Wang Jingquan, et al. Theoretical and experimental study on the transverse vibration properties of an axially moving nested cantilever beam[J]. Dermatologic Therapy, 2014, 333(13):48-51.

[16] Kobayashi N, Watanabe M. Dynamics and stability of spaghetti and reverse spaghetti problems coupled with fluid force[J]. Multibody System Dynamics, 2004, 11(2):111-125.

[17] Sugiyama S, Kobayashi N, Komaki Y. Modeling and experimental methods for dynamic analysis of the spaghetti problem[J], ASME Journal of Vibation and Acoustics, 2005, 127(1):44-51.

[18] 王亮，陈怀海，贺旭东，等. 轴向运动悬臂梁系统阻尼与边界条件试验[J]. 振动、测试与诊断, 2010, 30(5):547-551.

Wang Liang, Chen Huaihai, He Xuedong, et al. Test on damping and boundary condition of axially moving canti lever beam[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(5):547-551. (in Chinese)