APLCD-WPT在滚动轴承特征提取算法中的应用*

赵晓平， 周子贤， 王丽华， 张永宏， 陶润喆

(1.南京信息工程大学江苏省网络监控中心 南京，210044) (2.南京信息工程大学计算机与软件学院 南京，210044) (3.南京信息工程大学信息与控制学院 南京，210044)

引 言

滚动轴承是机械设备中应用最为广泛的部件，约30%的机械故障是由滚动轴承的损坏引发的[1]，因此，对滚动轴承的状态监测具有十分重要的意义。当轴承发生故障时会产生大量非平稳、非线性振动信号，时频分析方法因能提供非平稳信号在时域和频域的联合分布信息而应用广泛，典型的时频分析方法如短时傅里叶变换、小波变换等都存在缺乏自适应性的缺陷[2-3]。近年来，最具代表性的时频分析方法是Huang等[4]提出的经验模态分解(empirical mode decomposition，简称EMD)，EMD分解能够自适应地将信号分解到多个内禀模态函数分量，在多个领域得到广泛应用。Zheng等[5]提出一种新的自适应时频分析方法(local characteristic-scale decomposition，简称LCD)，LCD分解能够根据信号的局部时变特征自适应地分解信号，得到若干瞬时频率具有物理意义的内禀尺度分量[6]。由于LCD分解是基于数据本身的特征尺度参数，且只采用一次拟合，因此在提高计算效率、抑制端点效应和削弱模态混淆等方面效果更佳[7]。虽然LCD方法已在信号分析及机械故障诊断等领域取得较好效果，但LCD依然存在模态混淆问题[8]。

针对此问题，国内外很多学者提出了解决方法。Deering等[9]提出了通过添加掩膜信号的方法，均化原始信号的极值点分布，达到抑制模态混淆的目的。Wu等[10]提出的基于噪声辅助分析的总体平均经验模态分解(ensemble empirical mode decomposition，简称EEMD)，对原始信号加入多对噪声，分解后再总体平均作为提取特征，较好地抑制了模态混淆。这些抑制模态混淆的算法都对LCD方法的改进提供了思路。相较于EMD方法，LCD对噪声和间歇信号更敏感。因此，郑进德等[11]提出完备总体平均局部特征尺度分解(complete ensemble local characteristic-scale decomposition，简称CELCD)，通过向信号添加多对相反的白噪声再LCD分解取均值，提取出引起模态混淆的分量，然后对余量直接进行LCD分解，保证了分解的完备性，但该方法依然存在少量的模态混淆现象。

基于以上分析，笔者提出了基于小波包的APLCD-WPT时频分析方法。首先，对原始信号添加多对相反且幅值随频率变化的噪声，改善信号极值的分布情况；其次，对加噪信号进行LCD分解，将分解结果总体平均后得到ISC分量；最后，针对总体平均后存在的少量模态混淆现象，利用WPT的局部分析能力予以修正，将特征频率从混淆的ISC分量中提取出来。实测卧式螺旋离心机信号验证结果表明，APLCD-WPT方法保证提取分量满足ISC分量定义，克服模态混淆的同时保证了分解的完备性，能够实现特征信号的精确提取。

1 LCD与小波包理论

1.1 LCD理论

LCD方法假设任何一个复杂信号都可分解为若干瞬时频率具有物理意义的内禀尺度分量，即ISC之和[5]。对一维信号S(t)的LCD分解步骤简述如下。

1) 确定信号S(t)的极值点mk与mk所对应的时刻tk(k=1,2,…,M)，M为极值点个数。

2) 根据式(1)计算任意两个相邻的极大(或极小)值连线lk在tk时刻的函数值Ak，再计算Ak与tk时刻极值mk的差Lk，式中α的值一般取0.5

采用三次样条函数拟合(tk,Lk)得到均值曲线mli1，然后将mli1从原信号S(t)中分离

Si(t)=S(t)-mli1

(3)

3) 若Si(t)满足ISC判据条件，输出Si(t)并令ISC1=Si(t)，否则将Si(t)代替原始数据S(t)。重复步骤1和2多次，直到Si(t)满足ISC条件。Si(t)为第1个ISC分量，记ISC1=Si(t)，i=i+1。

4) 将ISC1分量从原始信号中分离出来，得到一个新信号作为输入信号，重复步骤1～3，得到ISC2，ISC3，…，ISCn，直到剩余信号单调或者能量与原始信号相比可忽略不计。这样将信号S(t)分解为n个内禀尺度分量和一个残余项r(t)之和，即

(4)

ISC分量必须满足两个条件：a.整个数据段内，任意相邻的两个极值点符号互异；b.令数据段内极值点为mk(k=1,2,…,N)，对应的时刻为tk。那么，由任意两个相邻的极大(或小)值点(tk,mk)，(tk+2,mk+2)确定的直线lk在tk+1时刻的函数值Ak+1与极值mk+1比值关系近似不变。

1.2 小波包理论

滚动轴承信号分析中，为解决特征提取后存在的少量模态混淆问题，可利用WPT[12]对各提取分量的细节部分进行修正，从而精确提取特征频率，便于准确判定故障类型[13]。

WPT是小波变换的推广，与小波变换不同的是WPT在对信号的低频部分进行分解的同时，对高频部分也进行了分解，具有更好的局部分析能力。小波包分解利用一组相关联的低通滤波器和高通滤波器，将信号分解成低频和高频两部分，通过多次分解达到所需要的频率区间。若分解的层数为l，则分解后的节点数为l2。小波包变换的二尺度方程为

(5)

其中：h0k，h1k为滤波器系数。

当n=0时，wo(t)为尺度函数，w1(t)为小波函数，{wn(t)}n∈Z为所确定的小波包。

小波包分系数的递推公式为

(6)

2 APLCD-WPT方法

虽然基于噪声辅助分析的方法对模态混淆有很好的抑制效果，然而LCD对噪声和间歇信号较为敏感，单纯添加白噪声的方法难以保证提取分量满足ISC定义。因此，笔者对LCD方法进行了改进，并针对提取分量存在少量模态混淆的问题，结合小波包理论提出APLCD-WPT方法。

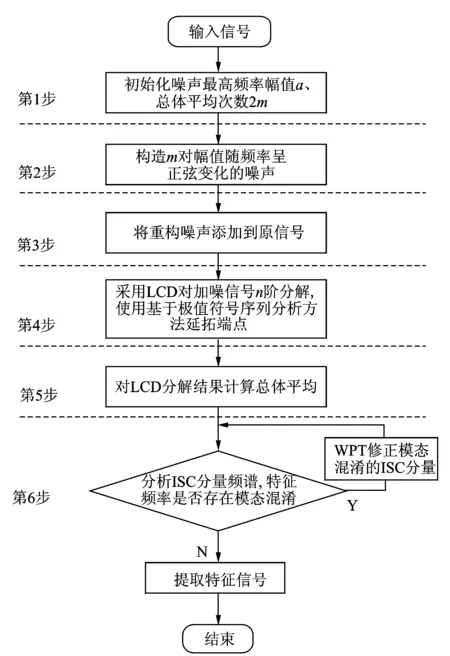
图1 APLCD-WPT方法流程图Fig.1 Flow chart of APLCD-WPT method

图1给出了APLCD-WPT算法流程，具体步骤如下。

1) 设输入信号为s(t)，初始化添加噪声的幅值a，总体平均次数为2m，其中m为添加噪声对的数量。

2) 构造幅值随频率呈正弦变化的噪声ns(t)。研究表明相比白噪声，加入幅值随频率变化的噪声对模态混淆的抑制效果更好[14]。噪声构造方法如下 ：首先，随机生成一组白噪声n(t)，将其进行傅里叶变换得到频谱N(f)，其中f∈(0,fs/2)，fs为采样频率；其次，令Ns(f)=N(f)sin(2π2f/fs)，构造噪声Ns(f)；最后，对Ns(f)进行逆傅里叶变换，得到幅值随频率呈正弦变化的噪声ns(t)。

3) 对原信号加入m对重构噪声ns(t)以及-ns(t)，组成加噪信号Si+(t)与Si-(t)，即

(7)

其中：i=1,2,…,m。

4) 对加噪信号Si+(t)，Si-(t)进行LCD分解，使用极值符号序列分析方法[15]延拓信号端点，记录每次分解的结果{ISCi+,n}和{ISCi-,n}，其中n为LCD提取的ISC分量个数。

5) 对2m组LCD分解结果进行总体平均，如式(8)所示，得到ISCn作为APLCD的分解结果

(8)

6) 检查特征频率分量是否存在模态混淆，如果依然存在少量模态混淆现象，再使用WPT进行修正，将特征频率从混淆的ISC分量中提取出来。

APLCD-WPT算法需要设置添加噪声的幅值a和噪声对的数量m。添加的白噪声如果幅值较小，无法达到影响信号极值点的分布，从而抑制模态混淆的目的；而过大的噪声则可能淹没原信号的特征信息，使得分解分量毫无意义。另一方面，虽然分解结果附带的噪声分量会随着总体平均次数的增加而逐步降低，但同时也会增加算法的计算量。目前，参数a和m虽然没有严格的选择依据，但文献[9]指出，a的幅值设为原信号幅值标准差的0.1～0.2倍，添加噪声的对数m选择100以内即可。

3 仿真试验

旋转机械工作时一般呈周期性运动，仿真分别用高、低频的谐波代表不同部件的旋转振动信号。当轴承出现故障时，往往伴随着调制与冲击成分，因此，仿真信号S包括冲击s1、高频余弦s2、调制s3和低频余弦s4共4个成分，如式(9)所示

S=s1+s2+s3+s4

(9)

其中：s2=cos(120πt)；s3=2sin(4πt)cos(50πt)；s4=cos(20πt-10)；采样时间t为1 s，采样频率为1 kHz。

混合信号及各成分时域波形如图2所示。

图2 仿真信号及各成分时域波形Fig.2 The time domain waveforms of simulation signal and components

分别采用LCD，CELCD和APLCD-WPT方法对混合信号进行分解。其中，ISC分量的判断采用三阈值准则，端点效应采用基于极值符号序列分析的方法处理。CELCD和APLCD-WPT算法均设置整体平均次数为100次，添加噪声幅值标准差为原信号幅值标准差的0.15倍。

图3 混合信号x的LCD分解结果Fig.3 The LCD decomposition results of simulation signal

图3为LCD分解结果，由图可以看出，受冲击信号影响，冲击信号s1与高频余弦s2都被分到ISC1分量，而调制信号s3和部分低频余弦信号s4被分到ISC2分量。结果证明LCD方法在处理含有冲击的信号时有严重的模态混淆问题，提取的特征分量难以反映原信号的特征频率，其应用范围具有局限性。

图4 混合信号x的CELCD分解结果Fig.4 The CELCD decomposition results of simulation signal

对信号进行CELCD分解，分解结果如图4所示。CELCD通过添加多对白噪声、分解后再总体平均的方法，能够有效减小分解误差。通过CELCD与LCD提取分量的比较，证明CELCD在一定程度上抑制了LCD分解的模态混淆问题。然而将CEL-CD提取的ISC3，ISC4分量与原信号进行比较，发现两者都出现局部波形失真的现象。其中，ISC3分量在波谷处部分失真，而ISC4的波形在峰值处也出现了轻微的畸变(如图中虚线圈部分)，说明CELCD方法提取的ISC分量依然存在少量模态混淆现象。

APLCD-WPT方法分解结果较理想，其中ISC1，ISC2，ISC3和ISC4分别对应原始信号中的s1，s2，s3和s4分量，基本上能正确反映出原始信号的特征。结果表明，APLCD-WPT方法不但克服了LCD分解产生的模态混淆问题，并且分解效果优于CELCD方法。APLCD-WPT方法分解结果见图5。

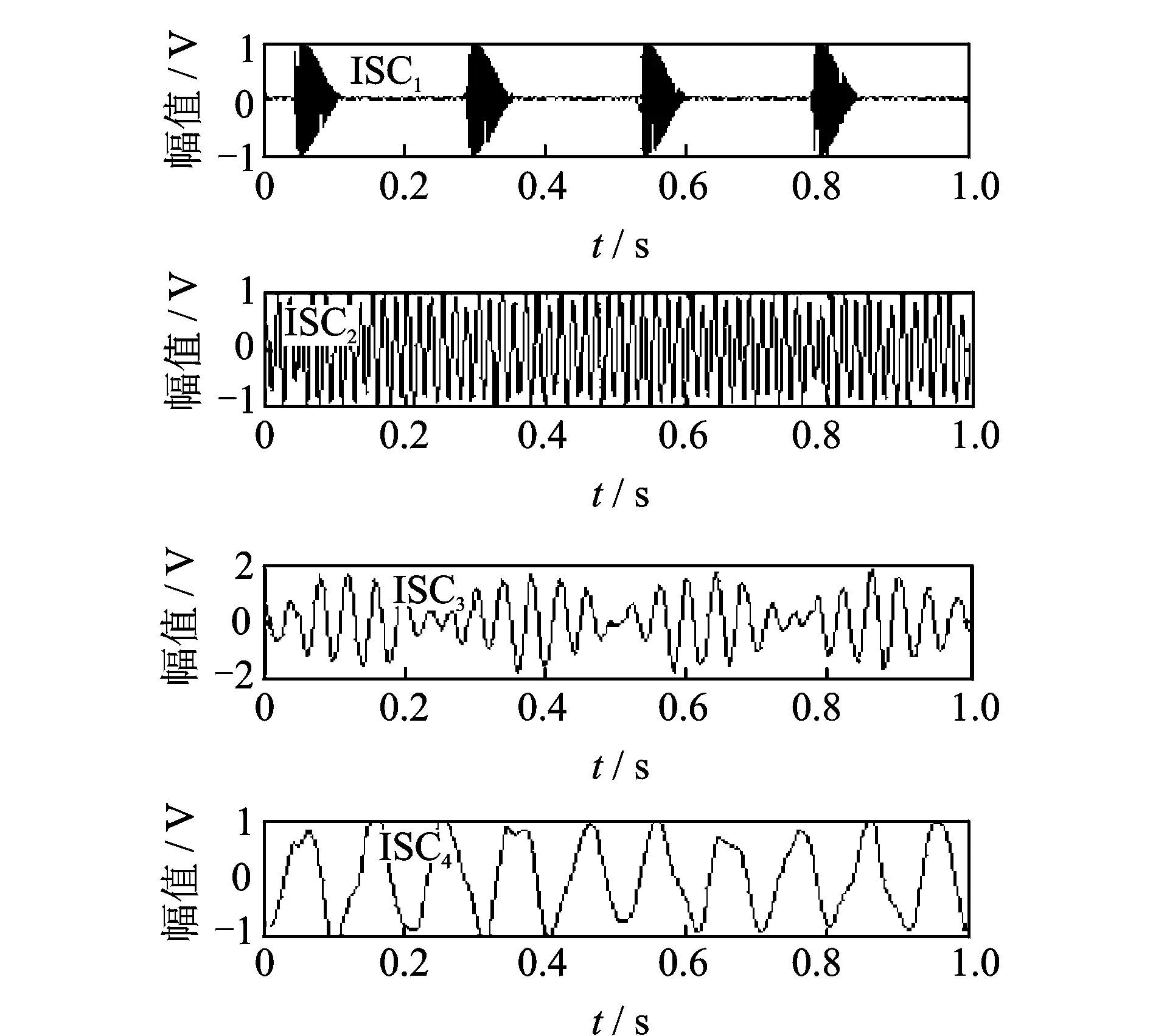
图5 混合信号x的APLCD-WPT分解结果Fig.5 The APLCD-WPT decomposition results of simulation signal

为了进一步比较LCD，CELCD和APLCD-WPT的分解效果，笔者还考察了每种方法提取分量与实际分量的相关性r与能量误差E这两个指标。其中，ri表示不同方法提取的分量ISCi与实际分量的相关系数；能量误差指提取分量与实际分量误差的能量与实际信号能量的比值，E越小说明提取的分量越接近实际值[16]。

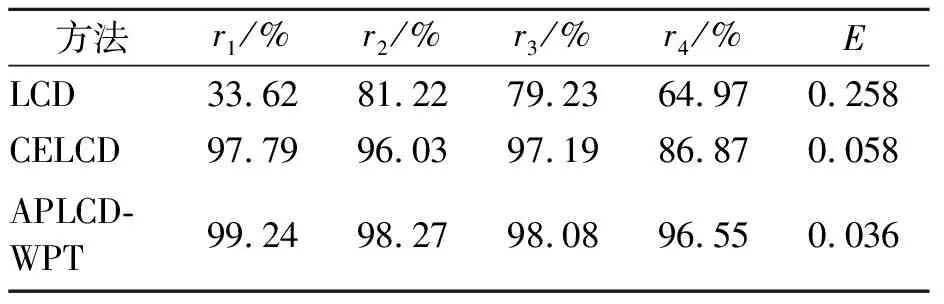
表1 LCD，CELCD和APLCD-WPT分解结果对比

由表1可以看出，LCD方法产生的模态混淆较为严重，提取分量与原信号的相关性较低。其中，冲击信号s1和低频余弦s4与原信号的相关性分别为33.62%和64.97%，无法满足特征提取的要求。CELCD方法提取分量与原信号的相关性都高于85%，说明CELCD方法相比LCD具有一定优越性。APLCD-WPT方法对提取的分量使用小波包进行了修正，因此得到的高频分量ISC1和ISC2与实际分量s1和s2的相关性比CELCD得到的相关性更高，且提取低频分量s4的相关性达到96.55%，远高于CELCD提取的低频分量。此外，APLCD-WPT与原信号计算得到的能量误差也小于CELCD方法。

上述仿真信号分析结果表明，APLCD-WPT方法不仅对间歇冲击引起的模态混淆现象有很好的抑制效果，相比现有的CELCD方法，其在提高特征精确度以及分量提取的完备性等方面都具有一定优势。

4 工程应用

为了进一步说明APLCD-WPT方法的有效性与实用性，将其应用于卧式螺旋离心机(简称卧螺离心机)运行阶段振动信号的分析[17]。卧螺离心机信号采用OROS R3X系的动态信号分析仪进行采集。

实验装置如图6所示。其中，振动传感器布置在左右轴承座处，能够从水平和垂直两个方向测量大端和小端的瓦振。同时，在大端和小端都安装支架固定电涡流传感器测量轴的振动，光电传感器装于转鼓大端。卧螺离心机的相关参数如表2所示。

图6 卧螺离心机大端传感器布置Fig.6 The big end sensor arrangement

取大端垂直方向轴振工作阶段的振动信号。综合考虑Nyquist采样定理与小波包分解理论，选择采样频率为12.8 kHz，采样时间为20 s。图7为其时域信号。

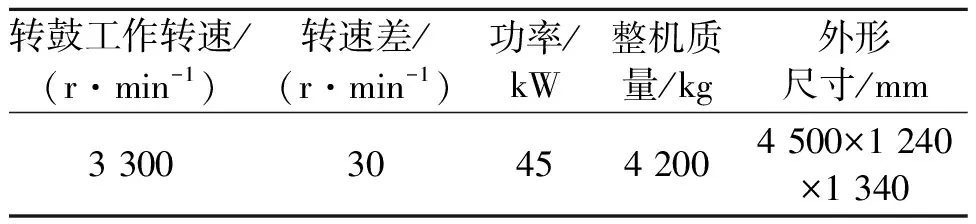
表2 卧螺离心机主要技术参数

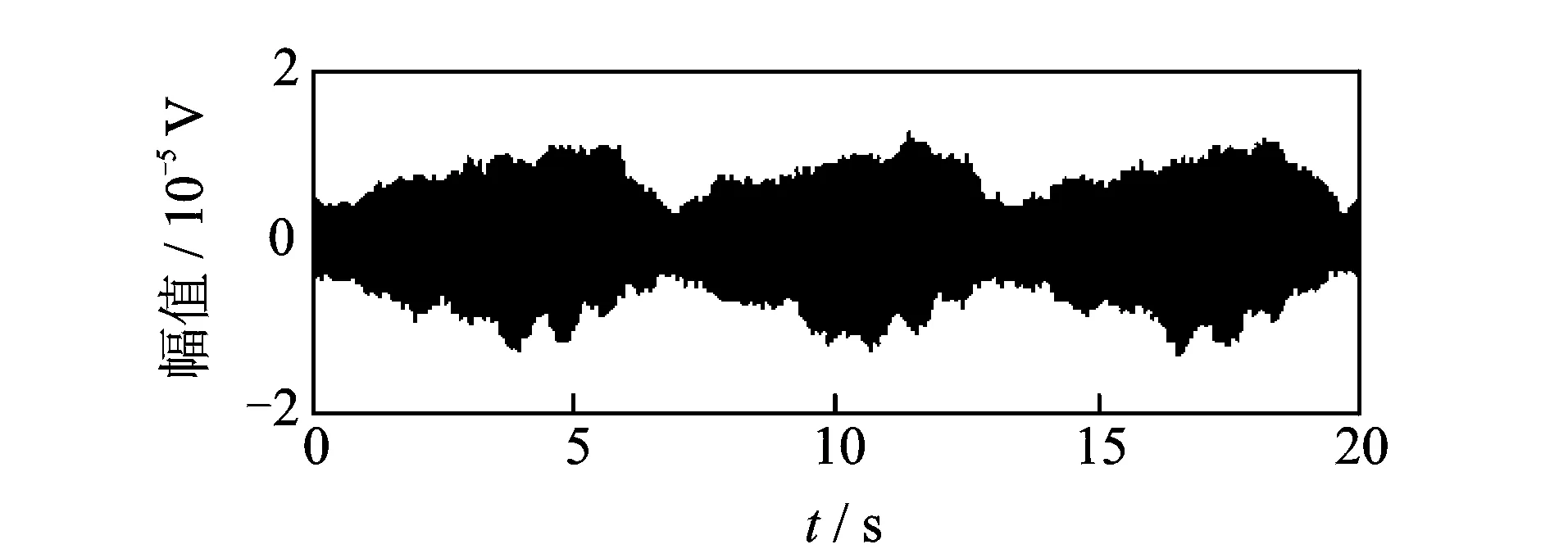
图7 振动信号时域图Fig.7 Vibration signal time domain diagram

通过对卧螺离心机频谱图进行分析，发现其主要频率成分有工作频率f(55 Hz)、2倍频和3倍频，其他多个频率成分难以识别，如图8所示。为此，采用APLCD-WPT算法对时域信号进行分解，提取55 Hz特征频率信号，设置整体平均次数均为50，添加噪声幅值标准差为原信号幅值标准差的0.15倍。

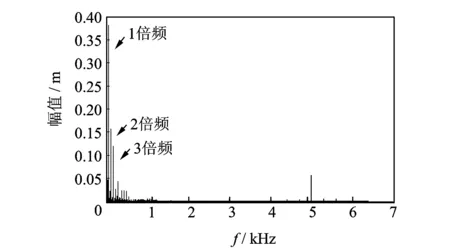
图8 振动信号频谱图Fig.8 Vibration signal spectrum

图9为信号仅经过APLCD分解后的频谱图(只列出分解后特征频率信号55 Hz存在模态混淆的3个ISC分量)，表明信号经APLCD分解后依然存在部分模态混淆现象。为了实现特征频率的精确提取，需要使用WPT对上述3个分量进行修正。对特征频率f使用WPT进行提取时，为了减小虚假分量的生成，小波包频段分割的下限应该低于f，同时上限要尽可能高于f且低于需剔除的频率。

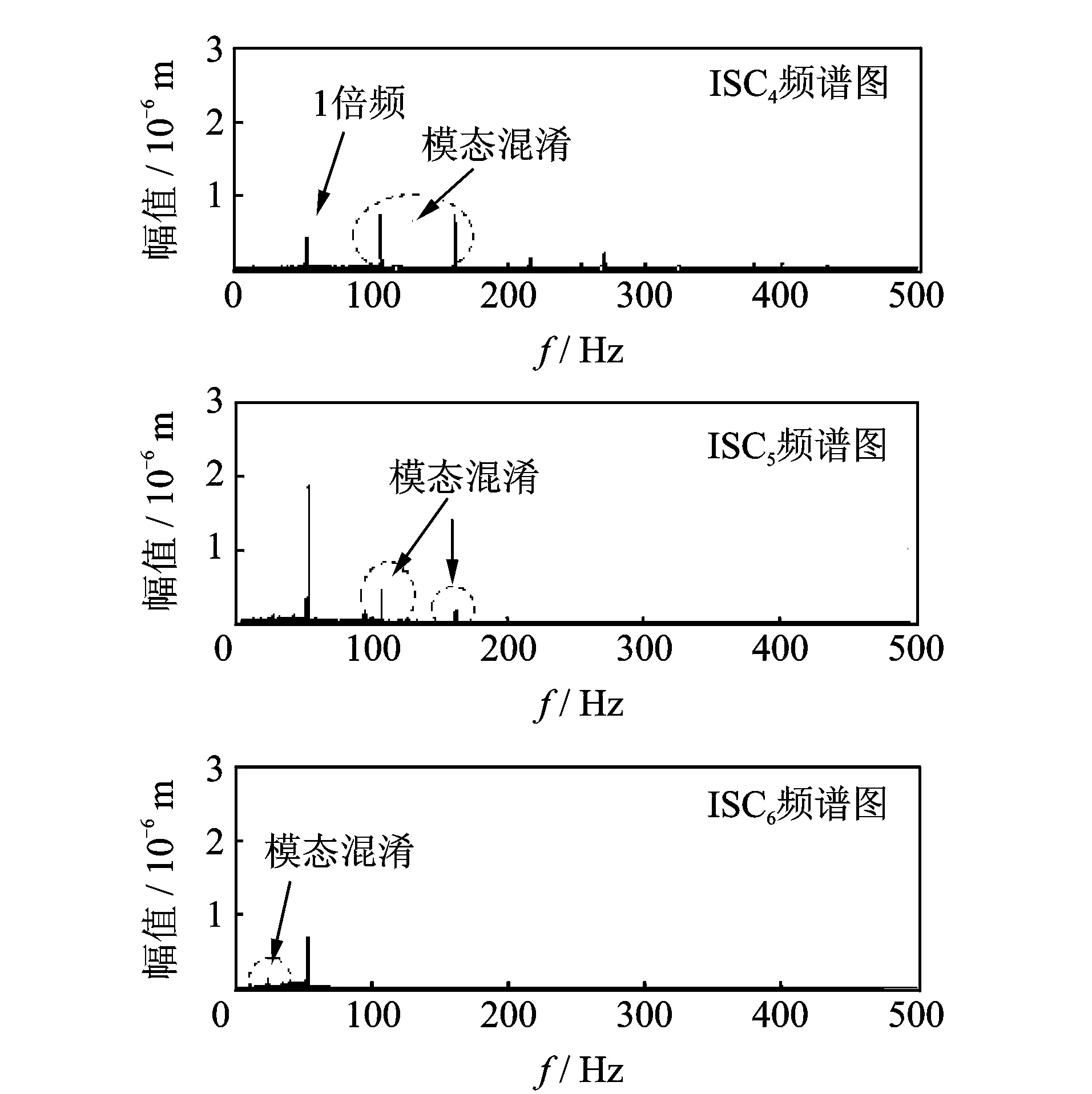
图9 ISC4，ISC5和ISC6分量频谱图Fig.9 The ISC4，ISC5 and ISC6 components spectrum

以ISC4为例，使用WPT消除图9中模态混淆的分量，需要将ISC4左侧模态混淆部分55 Hz分量提取出来。因为信号采样频率为12.8 kHz，而55 Hz太靠近WPT7层分解提取50～100 Hz频率区间的分割处，直接进行WPT提取易产生虚假分量。因此，首先对ISC4进行WPT6层分解，提取出0～100 Hz频率段的分量I1；其次再对ISC4进行WPT8层分解，提取出75～100 Hz分量I2；最后用WPT6提取的分量I1减去WPT8提取的I2，从而将55Hz分量从模态混淆的ISC4中提取出来。

同样，将特征分量f从ISC5和ISC6中提取出来。其中，对应ISC5先进行WPT6层分解，提取出0～100 Hz频率段的分量I3；再对ISC5进行WPT8层分解，提取出75～100 Hz分量I4；最后将I3减去I4，提取出ISC5中混淆的55 Hz分量。处理ISC6时只需将提取的0～100Hz频率段分量I5减去WPT8层分解得到0～25 Hz分量I6，同样能够将模态混淆ISC6中的55 Hz分量提取出来。ISC4，ISC5和ISC6使用WPT提取分量的频谱图如图10所示。

图10 APLCD-WPT提取的ISC4，ISC5和ISC6频谱图Fig.10 The ISC4，ISC5 and ISC6 components spectrum of APLCD-WPT

将ISC4，ISC5和ISC6提取分量相加，得到特征频率55Hz的分量，其频谱图如图11所示。由图可以看出，APLCD-WPT方法很好地将模态混淆部分进行了消除，能够有效地提取出特征频率信号。

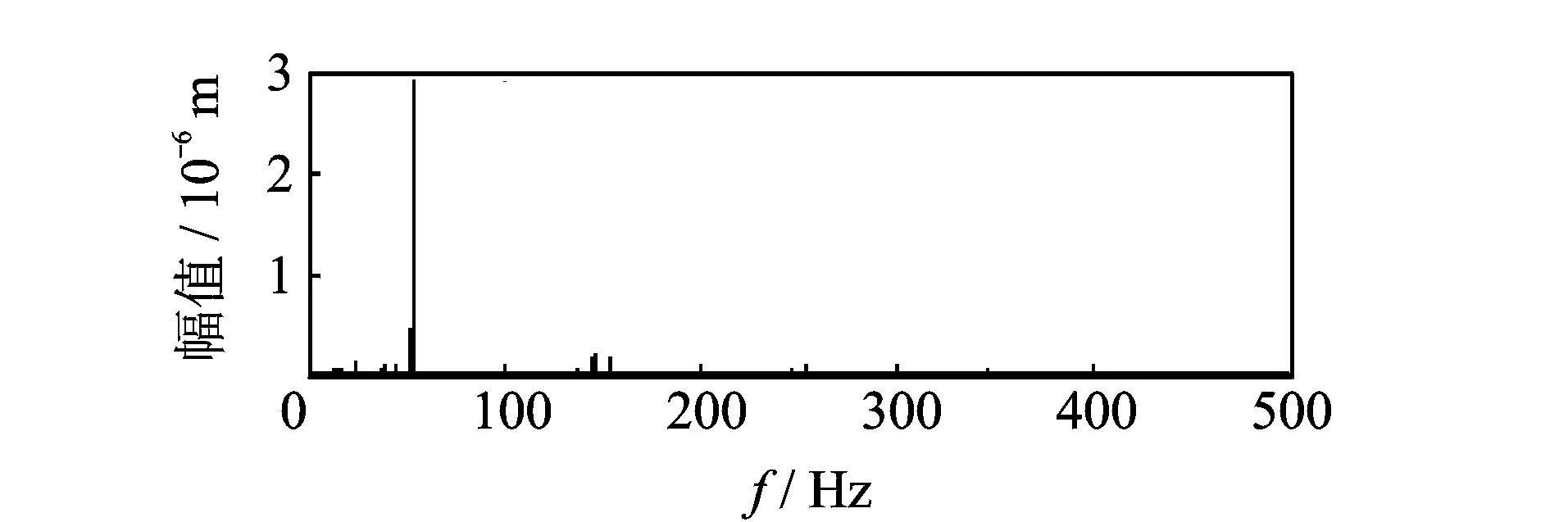
图11 APLCD-WPT提取的特征信号频谱图Fig.11 The signal spectrum of APLCD-WPT

将LCD，CELCD和APLCD-WPT这3种方法提取得到的55Hz时域信号进行对比分析，如图12所示。通过比较发现，LCD方法不但存在模态混淆的问题，而且混入的噪声使得提取分量不如APLCD-WPT提取的分量平滑。CELCD方法提取的分量存在少量模态混淆的问题，得到的55Hz分量的信号周期性较差，很难满足单一频率信号的精确提取。此外，APLCD-WPT方法提取的分量与CELCD和LCD提取的分量相比幅值更小，且更具有周期性，可以实现特征频率的精确提取。综上所述，APLCD-WPT方法不仅能解决提取分量模态混淆的问题，还能很好地实现特征信号的自适应提取。

图12 LCD，CELCD和APLCD-WPT方法提取分量时域图Fig.12 The time domain diagram result of LCD，CELCD and APLCD-WPT

5 结束语

为了有效提取滚动轴承特征频率信号，提出了一种基于APLCD-WPT的滚动轴承特征提取方法。该方法通过APLCD筛选出滚动轴承特征频率分量，然后结合WPT方法修正提取ISC分量中模态混淆的部分，实现了滚动轴承特征频率信号的精确提取。将所提方法应用于仿真和实测数据分析，结果表明，APLCD-WPT不但能够抑制模态混淆，且较传统时频分析算法，对滚动轴承信号特征具有更好的提取效果，有利于后期的状态监测和故障诊断。

参 考 文 献

[1] 钟秉林，黄仁. 机械故障诊断学[M].北京：机械工业出版社，2007:1-5.

[2] Cohen L. Time-frequency distribution-a review[J]. Proceedings of the IEEE，1989，77(7)：941-981.

[3] Mallat S G. A theory for multi-resolution decomposition， the wavelet representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1989，11(7)：674 -689.

[4] Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for non- linear and non-stationary time series analysis[J]. The Royal Society，1998，454：903-995.

[5] Zheng Jingde，Cheng Junsheng，Yu Yang. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy[J]. Mechanism and Machine Theory，2013，70(6)：441-453.

[6] 杨宇，曾鸣，程军圣. 局部特征尺度分解方法及其分量判据研究[J]. 中国机械工程，2013，24(2)：195-201.

Yang Yu，Zeng Ming，Cheng Junsheng. Research on local characteristic-scale decomposition and its stopping criteria[J]. China Mechanical Engineering，2013，24(2)：195-201. (in Chinese)

[7] 杨宇，曾鸣，程军圣. 局部特征尺度分解方法及其分解能力研究[J]. 振动工程学报，2012，25(5)：602-609.

Yang Yu，Zeng Mine，Cheng Junsheng. Research on local characteristic-scale decomposition and its capacities[J]. Journal of Vibration Engineering，2012，25(5)：602-609. (in Chinese)

[8] 胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断，2011，31(4)：429-434.

Hu Aijun，Sun Jingjing，Xiang Ling. Mode mixing in empirical mode decomposition[J]. Journal of Vibration，Measurement & Diagnosis，2011，31(4)：429-434. (in Chinese)

[9] Deering R，Kaiser J F. The use of masking signal to improve emprical mode decomposition[C]∥IEEE International Conference on Acoustics，Speech，and Signal Processing. Philadelphia，USA:[s.n.],2005.

[10] Wu Z，Huang N E. Ensemble empirical mode decom- position：a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis，2009，1(1)：1-41.

[11] 郑近德，程军圣，聂永红. 完备总体平均局部特征尺度分解及其在转子故障诊断中的应用[J]. 振动工程学报，2014，27(4)：637-644.

Zheng Jinde，Cheng Junsheng，Nie Yonghong，et al. Complete ensemble local characteristic-scale decomposi- tion and its applications to rotor fault diagnosis[J]. Journal of Vibration Engineering，2014，27(4):637-644. (in Chinese)

[12] 张建宇，张随征，管磊，等. 基于小波包变换和样本熵的滚动轴承故障诊断[J]. 振动、测试与诊断，2015，35(1)：128-132.

Zhang Jianyu，Zhang Suizheng，Guan Lei，et al. Pattern recognition of bearing defect severity based on multiwavelet packet sample entropy method[J]. Journal of Vibration，Measurement & Diagnosis，2015，35(1)：128-132. (in Chinese)

[13] 王丽华，陶润喆，张永宏，等. 基于CEEMD-WPT的滚动轴承特征提取算法[J]. 振动、测试与诊断，2017，37(1)：181-188.

Wang Lihua，Tao Runzhe，Zhang Yonghong，et al. Feature extraction of rolling bearing based on CEEMD- WPT[J]. Journal of Vibration，Measurement & Diagnosis，2017，37(1)：181-188. (in Chinese)

[14] 雷亚国，孔德同，李乃鹏，等. 自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J]. 机械工程学报，2014，50(3)：64-70

Lei Yaguo，Kong Detong，Li Naipeng，et al. Adaptive ensemble empirical mode decomposition and its application to fault detection of planetary gearboxes[J]. Journal of Mechanical Engineering，2014，50(3)：64-70. (in Chinese)

[15] 徐卓飞，刘凯. 基于极值符号序列分析的EMD端点效应处理方法[J]. 振动、测试与诊断，2015，35(2)：309-315.

Xu Zhuofei，Liu Kai. Method of empirical mode decomposition end effect based on analysis of extreme value symbol sequence[J]. Journal of Vibration，Measurement & Diagnosis，2015，35(2)：309-315. (in Chinese)

[16] Frei M G，Osorio I. Intrinsic time-scale decomposition：time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society a Mathematical Physical & Engineering Sciences，2007，463(2078)：321-342.

[17] 赵晓平，侯荣涛. 基于Viterbi算法的Gabor阶比跟踪技术[J]. 机械工程学报，2009，45(11)：247-252.

Zhao Xiaoping，Hou Rongtao. Gabor order tracking based on viterbi algorithm[J]. Journal of Mechanical Engineering，2009，45(11)：247-252. (in Chinese)