基于CS-BBO优化SVM的汽轮机转子故障诊断*
2018-07-31石志标葛春雪
石志标, 葛春雪
(东北电力大学机械工程学院 吉林,132012)
引 言
汽轮机是工业生产中的重要设备,因其运行环境复杂,所以容易出现不可预知的事故。尤其是转子,一个微小的故障就可能影响整个系统的安全运行。国内外曾发生过多起因为汽轮机转子故障而导致的重大事故,对社会经济造成严重影响。因此,对汽轮机转子进行准确快速的故障诊断研究具有十分重要的现实意义[1]。
支持向量机是一种优于神经网络的机器学习算法,具有良好的推广能力,能较好地解决小样本、非线性等问题[2-3]。但SVM在具体应用过程中学习能力和泛化能力是由其参数决定的,因此,对其参数的优化问题显得尤为重要。目前,一般采用遗传算法、粒子群算法及退火算法等对SVM的参数进行优化,但这些算法都存在各自的不足。如遗传算法易陷入局部最优、收敛速度慢[4];粒子群算法虽然收敛速度快,但局部搜索能力差,易陷入局部最优[5]。BBO算法与其他优化算法相比,具有搜索精度高、自适应能力强、参数少及实现简单等优点,能够有效地解决全局优化问题[6],并在函数优化、飞机传感器检测及卫星图像识别问题等实际工程优化问题求解中获得较为成功的应用。
为提高支持向量机的故障识别准确率和识别效率,首先,将BBO算法与混沌思想相结合,得到一种新型混合算法CS-BBO;其次,利用CS-BBO算法对支持向量机的惩罚因子c和核函数参数σ进行优化,得到最优诊断模型;最后,通过ZT-3转子试验台模拟汽轮机转子故障,得到试验数据,验证所提出的CS-BBO算法优化SVM模型的有效性,并与BBO算法优化SVM模型对比其在汽轮机转子4种状态下的识别准确率和识别效率。
1 支持向量机
1.1 支持向量机原理
支持向量机是一种以统计学为基础、以结构风险最小化为原则的机器学习方法,对解决小样本、非线性及高维复杂问题等方面具有明显的优势[7]。SVM能够通过对有限的样本进行学习而获得具有较强泛化能力的决策函数,其表达形式为
(1)
其中:αi为拉格朗日乘子;xi,xj为输入向量;yi为对应期望输出;b为偏置常数;K(xi,xj)为核函数。
SVM中常用的核函数有径向基核函数(radial basis function, 简称RBF)、多项式核函数和Sigmoid核函数[8-9]。其中,RBF核函数只包含参数σ,对其优化较为简单,有利于参数优化。因此,笔者选用RBF核函数作为SVM函数,其函数形式为
(2)
得到的最优分类超平面为
(3)
1.2 支持向量机参数
支持向量机的参数对其学习能力和泛化能力有着十分重要的影响,为使支持向量机能够更好地进行故障识别,需要对支持向量机的参数进行优化。
笔者采用的是SVM模式识别软件包LIBSVM,应用该软件可以快速有效地解决大部分问题,而且不需要太多地调整参数。
在SVM参数中,RBF核函数中包含一个参数σ,当σ较小或较大时,支持向量机的算法推广能力和分类能力会变差[10]。惩罚因子c的作用是在错分样本数量和算法复杂程度之间寻求一个平衡点。在数据子空间确定的前提下,通过调整算法中经验风险和置信范围比例的大小,改变分类器的推广能力。当c取值较小时,对经验误差的惩罚力度会减小;当c取值较大时,对经验误差的惩罚力度也随之增大[5]。
2 CS-BBO算法优化SVM参数
2.1 生物地理学优化算法
生物地理学优化算法是一种以遗传算法和粒子群算法为基础的新型智能全局优化算法[11]。其基本思想源于生物地理学理论,通过模拟生物群体中相邻个体的迁徙和特别个体的变异来进行信息交流,寻找全局最优解[6]。
2.1.1 迁移操作
常见的单个栖息地物种迁移率模型有4种:线性迁移率模型、二次迁移率模型、指数迁移率模型和余弦迁移率模型[12]。为了更准确地模拟生物地理环境中物种迁移过程,笔者采用更符合自然规律的余弦迁移率模型进行计算,如图1所示。
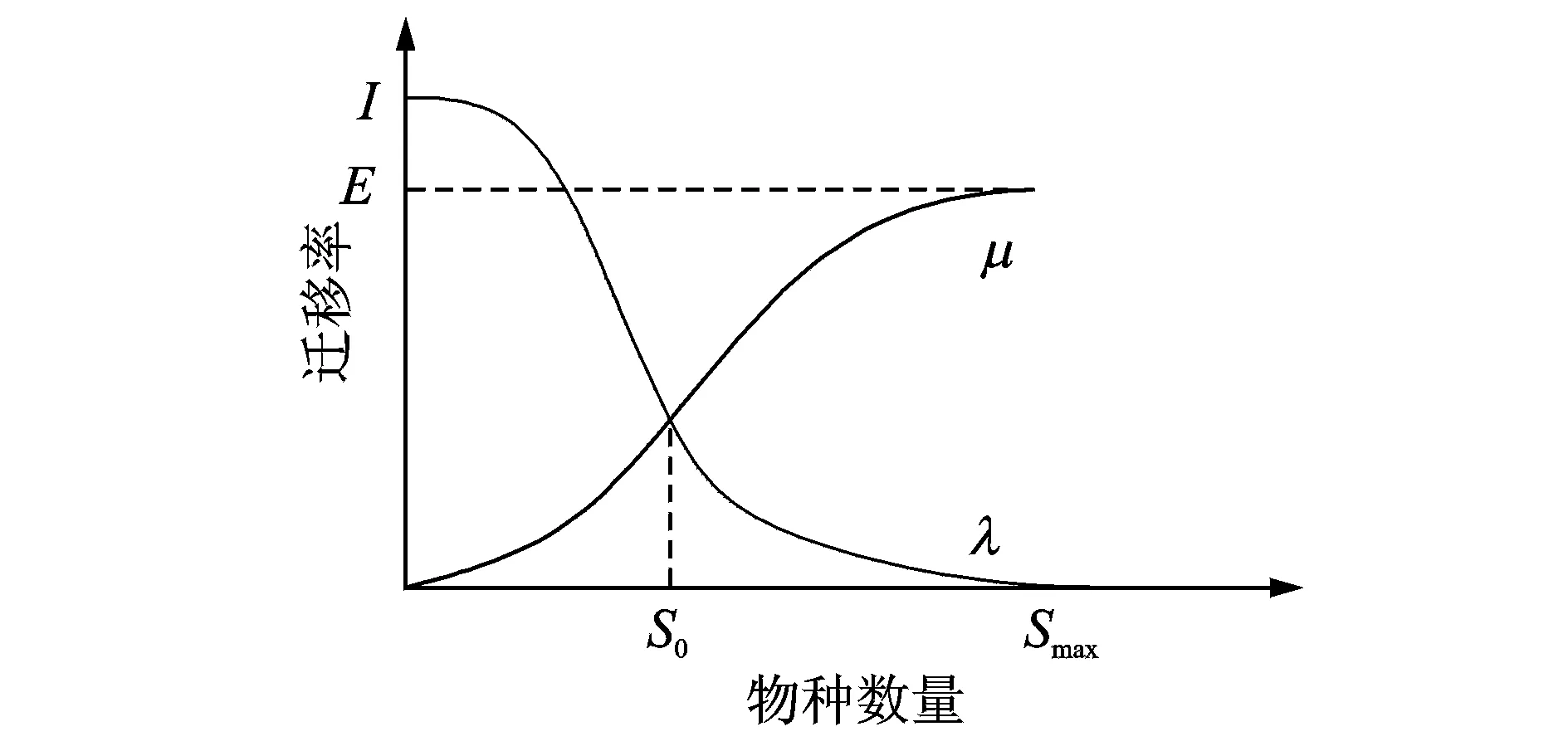
图1 余弦迁移率模型Fig.1 Cosine migration rate model
其中:I为最大迁入率;E为最大迁出率;Smax为该栖息地所能容纳的最大物种数量;λ为迁入率;μ为迁出率;S0为平衡点。
设当Smax=n,栖息地存在的物种数目为k时,该栖息地的迁入率λk、迁出率μk分别为
BBO算法是通过栖息地适宜指数(habitat suitability index, 简称HSI)所对应的适宜度函数来对栖息地进行评价。与HSI相关的特征因子如降雨量、温度和湿度等自然因素,用适宜度向量(suitable index vector, 简称SIV)表示,因此,可以通过解决适宜度最优化问题来寻求最优解。
在迁移操作过程中,BBO算法通过个体迁移算子来进行信息的共享,个体通过对各自的迁入、迁出概率进行计算来确定个体信息的迁移概率。执行迁移操作时,首先,计算每个栖息地的HSI值,并按照从大到小依次排序;其次,根据迁入率λ确定待迁入栖息地,再根据迁出率μ确定需要与之互换的相邻栖息地;然后,从相邻栖息地中随机选取一个SIV替代该栖息地中的一个SIV;最后,计算出每个栖息地的HSI值并进行排序,最高HSI点对应最优解。
2.1.2 变异操作
栖息地的生态环境会受自然因素影响发生突变,物种种类和数量也会随之发生变化。BBO算法中通过变异操作来提升物种的多样性,为算法提供更多的搜索目标。栖息地的变异率与物种数量成反比,即
(6)
其中:mmax为最大变异率;P(s1)为栖息地中物种数量为S1所对应的概率;Pmax为PS的最大值。
PS与迁入率λ、迁出率μ的关系如下
(7)
在BBO算法中,如果某个栖息地的变异概率ms为非零值,则根据变异操作随机产生一个SIV,取代该栖息地已有的SIV,以此来增加物种的多样性,提升栖息地的解集,得到最优解。
2.2 混沌生物地理学优化算法
由于混沌运动具有强大的遍历性和随机性,因此用混沌对BBO算法进行优化,得到CS-BBO算法,可以提高群体遍历性,增加搜索精度,并加快收敛速度。
2.2.1 CS-BBO算法的优化原理
采用文献[13]提出的分段Logistic混沌映射对BBO算法进行优化,方程如下
(8)
当μ=4时,映射方程完全处于混沌状态,所以μ取值为4。
利用分段Logistic混沌映射对种群进行初始化。首先,随机产生一个初始向量Xi=(xi1,xi2,…,xil),其中l为目标函数解的维度;其次,通过式(8),得到N个向量X1,X2,…,Xn,并将X1,X2,…,Xn变换到所优化的目标函数中初始变量的取值区间;最后,分别计算目标函数中每个初始变量的适宜度值,选取前M个适宜度值较高的作为BBO算法的初始种群。
为保证解的多样性,取得好的优化效果,利用分段Logistic混沌映射在已有解的基础上进行混沌搜索。首先,设已有解中搜索到的最优解为Jbest,混沌搜索次数为T,以Jbest为基础进行混沌搜索,即
Jn=Jbest+wXi
(9)
其中:Xi为混沌映射方程(8)的解;w为调整系数。
调整w是为了扩大解的范围,使得原本均为正数的解变得有正有负。其取值情况如下

(10)
通过混沌变量产生一组Jbest的邻域解Ibest=(I1,I2,…,Im),对每一个解计算其HSI值,若Ibest中的最优解的HSI值优于Jbest中的HSI值,则用Ibest代替Jbest成为全局最优解,否则保持不变。
2.2.2 CS-BBO算法的优化测试
为验证CS-BBO算法的优化性能,笔者利用Griewank和Rastrigin测试函数对算法的优化性能进行仿真测试[14]。测试函数定义如表1所示。

表1 测试函数
两种测试函数的迭代寻优过程如图2所示,其中:BBO算法对Rastrigin和Griewank函数的训练时间分别为7.771和17.134s;CS-BBO算法对Rastrigin和Griewank函数的训练时间分别为3.713和9.828s。由图2可以看出,在Rastrigin和Griewank函数迭代过程中,CS-BBO算法的寻优曲线较BBO算法的寻优曲线能更快进入最优解区间,且状态稳定。
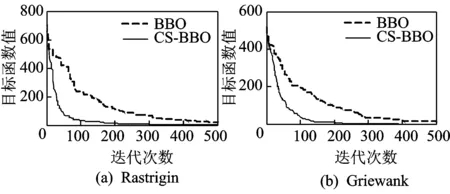
图2 BBO算法和CS-BBO算法测试函数训练曲线Fig.2 Benchmark function training curves of BBO and CS-BBO algorithms
2.3 CS-BBO算法的SVM参数优化
笔者所采用的RBF核函数支持向量机的待优化参数为σ和c,为提高SVM的分类准确率和识别效率,利用CS-BBO对SVM参数进行优化。设CS-BBO的适宜度函数为分类准确率,即
(11)
其中:ltn为第n个测试集中的正确分类个数;ln为测试集中样本的个数。
其优化步骤如下:
1) CS-BBO算法参数的设置,如混沌搜索次数T、栖息地能容纳的最大物种数目Smax、最大迁入率Imax、最大迁出率Emax及迭代次数等;
2) 利用混沌对一组栖息地进行初始化,令该栖息地的初始适宜度向量为Xi,Xi中包含SVM的参数σ和参数c;
3) 将每个栖息地设为当前个体最优解,并分别计算适宜度值f(i),把f(i)映射给每个物种,取适宜度最好的栖息地中的最优个体作为最初的全局最优解;
4) 对每个栖息地分别计算迁入率和迁出率,判断栖息地是否发生迁移操作,若发生迁移操作,则通过轮盘赌的方式确定替换栖息地,从而对栖息地进行修改;
5) 对栖息地进行变异操作,通过更新物种来保持解的多样性;
6) 最后进行混沌搜索,通过重新计算适宜度向量Xi,保留最优解;
7) 将得到的优化初值作为SVM最优诊断模型中的参数σ和参数c。
其优化流程图如图3所示。
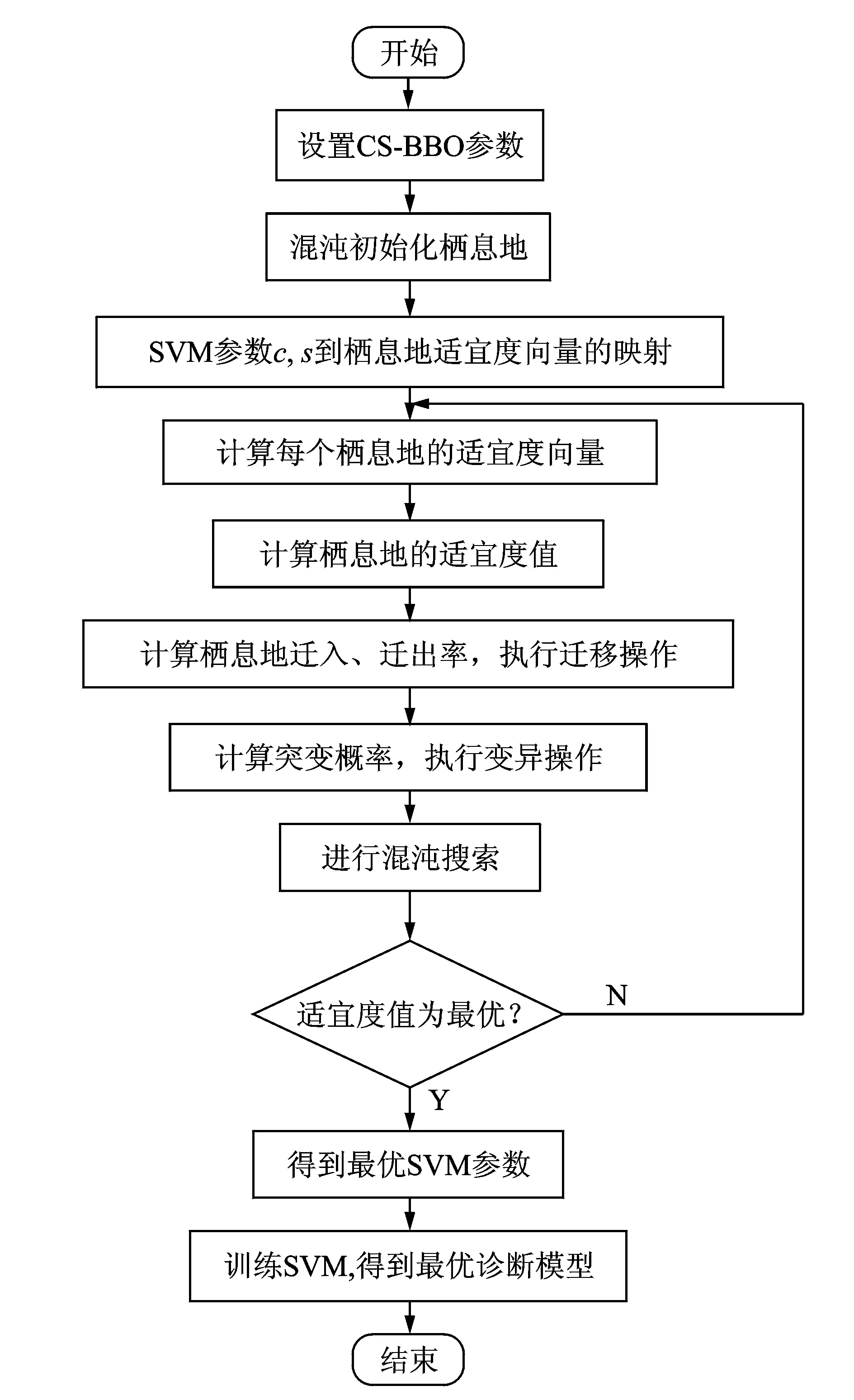
图3 CS-BBO算法优化SVM参数流程图Fig.3 Flow chart for CS-BBO algorithm to optimize SVM parameters
3 转子故障诊断分析研究
3.1 试验数据
为了验证笔者提出的基于CS-BBO算法优化SVM的汽轮机转子故障诊断的有效性与先进性,采用ZT-3转子振动模拟试验台进行故障模拟试验,分别模拟汽轮机转子处于正常状态及3种常见故障状态,即转子不平衡、转子不对中、动静碰磨。试验设备如图4所示。

图4 ZT-3转子振动模拟试验台Fig.4 ZT-3 simulation experiment bench of rotor vibration
设置转速为3 kr/min,采样频率为5 kHz,并采集振动信号。下面以转子处于正常状态和动静碰磨状态为例,其原始振动信号如图5所示。
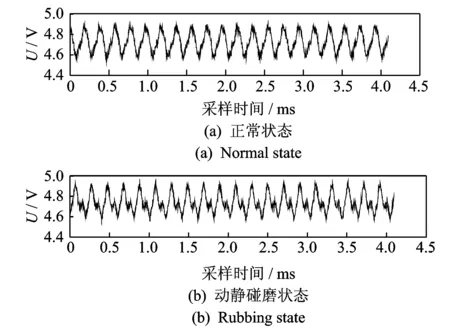
图5 正常状态和动静碰磨状态的原始振动信号图Fig.5 Original vibration signals of normal and rubbing states
采用软阈值小波降噪方法对采集到的原始振动信号进行降噪[15-16]。降噪后,正常状态和动静碰磨故障状态的降噪信号图如图6所示。
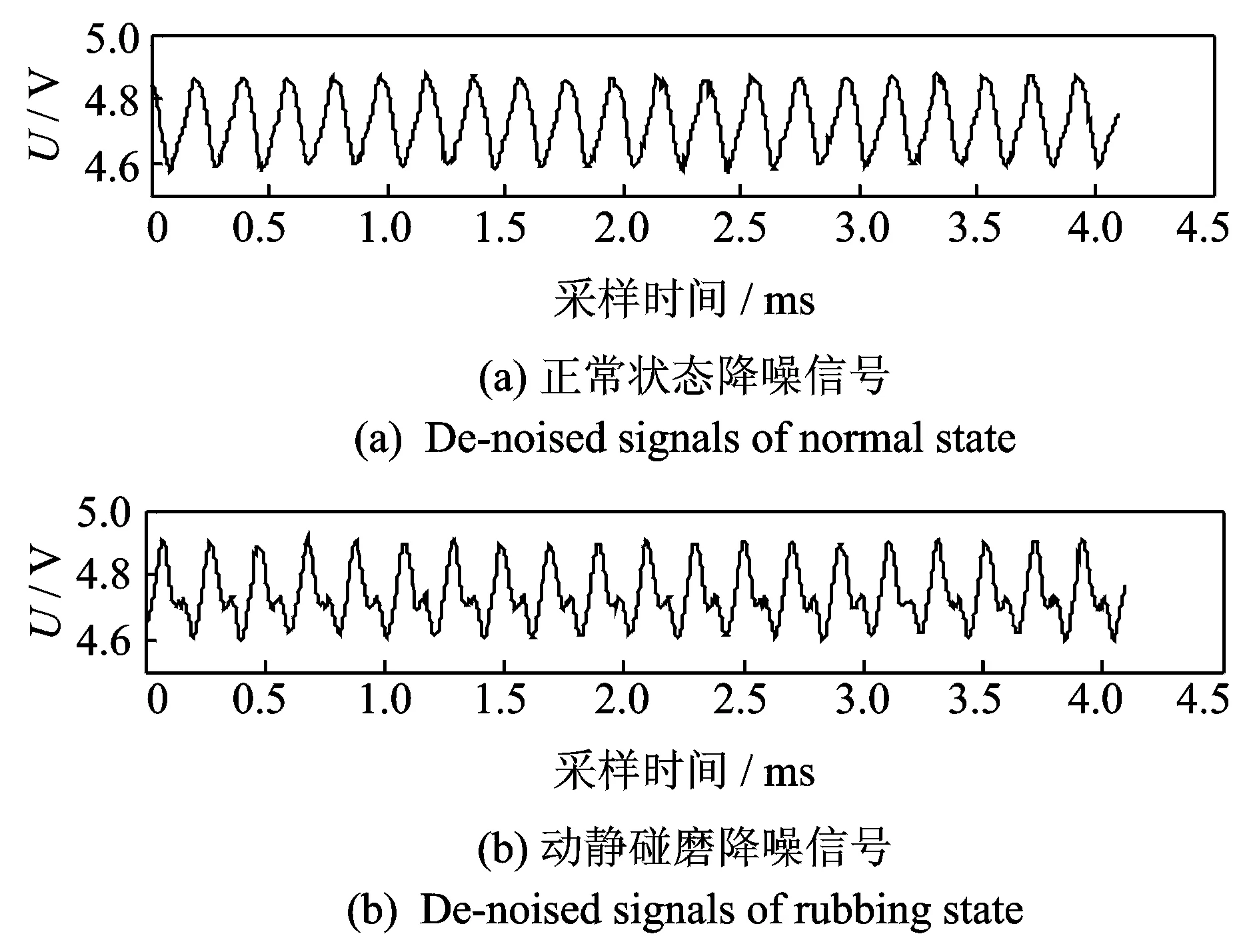
图6 正常状态和动静碰磨状态的降噪信号图Fig.6 De-noised signals of normal and rubbing states
通过信噪比(signal noise ratio, 简称SNR)[17]改善量ΔSNR验证降噪效果,降噪后,正常状态、动静碰磨、转子不对中及转子不平衡的信噪比分别为18.234 4,19.361 6,21.621 4,18.316 9。
3.2 特征提取
局部均值分解法(local mean decomposition, 简称LMD)是一种新型的自适应时频分析方法[18]。其本质是从原始信号中分离出纯调频信号和包络信号,相乘后得到一系列瞬时频率具有物理意义的乘积函数(production function, 简称PF),通过组合所有PF分量,得到完整的原始信号的时频分布[19]。以转子处于正常状态和动静碰磨故障状态为例,对其进行LMD分解后所得的PF分量如图7、图8所示。

图7 正常状态转子振动的LMD分解结果Fig.7 LMD decomposition result of rotor vibration under normal state

图8 动静碰磨状态转子振动的LMD分解结果Fig.8 LMD decomposition result of rotor vibration under rubbing state
依次提取各个PF分量的均值、均方根值、均方根误差、标准差、峰值、峭度、裕度指标、脉冲指标、峰值指标及波形指标等特征值,并通过直方图对比4种故障状态的区分程度,以4种状态LMD分解后PF1分量提取的特征值为例,如图9所示。

图9 转子4种状态PF1分量特征值区分程度Fig.9 Distinguishing degree of component characteristic value of PF1 under 4 states
由图9可以看出,均方根值、峭度、脉冲指标及峰值指标对4种状态的区分程度较好。以脉冲指标为例,4种故障的箱线图如图10所示。

图10 转子4种状态脉冲指标箱线图Fig.10 Pulse index boxplot of 4 states rotor
图10中:箱线图的高度表示25%位数到75%位数的距离;箱线图中的横线表示中位数的数值大小;+表示存在的异常值[20]。由图10可以看出,利用脉冲指标作为特征值构造特征向量区分效果明显。同理,均方根值、峭度、峰值指标均可作为故障识别特征。因此,笔者采用上述4种特征作为故障特征,对各类故障类型经LMD分解后,选取前两个PF分量,并构造特征向量,特征向量的维数均为8。
3.3 故障识别与比较
二分类支持向量机是构造多分类的基础,在解决多分类问题时,主要方法是将多个二分类SVM进行组合。常用的多分类方法有“一对多”、“一对一”、“二叉树”等[21]。笔者采用的是“一对多”多分类方法来识别转子系统的4种状态。
为验证CS-BBO算法优化SVM诊断模型的有效性与先进性,与BBO算法优化SVM的训练和诊断结果进行比较。采用转子常见的4种状态数据(正常状态、转子不平衡、转子不对中和动静碰磨)为试验数据,每类故障选取40组样本,共160组样本,从中随机选取112组样本进行训练,剩余48组样本进行测试。CS-BBO算法初始参数设置如表2所示。

表2 CS-BBO算法参数
图11为CS-BBO算法和BBO算法对SVM的故障诊断模型进行参数优化的适宜度曲线。其中,适宜度均值曲线表示所有种群在每一代中的平均适宜度值,适宜度最优值曲线表示所有种群在每一代中的最大适宜度值。由图11可知,CS-BBO算法在第13,20,53代多次跳出局部最优后,在第54代,收敛水平趋近一致,达到最大适宜度;BBO算法在7,25代跳出局部最优后所达到的最大适宜度要低于CS-BBO算法所达到的最大适宜度。至此,两种算法均可对SVM参数进行优化,但CS-BBO算法的优化能力明显强于BBO算法的优化能力。
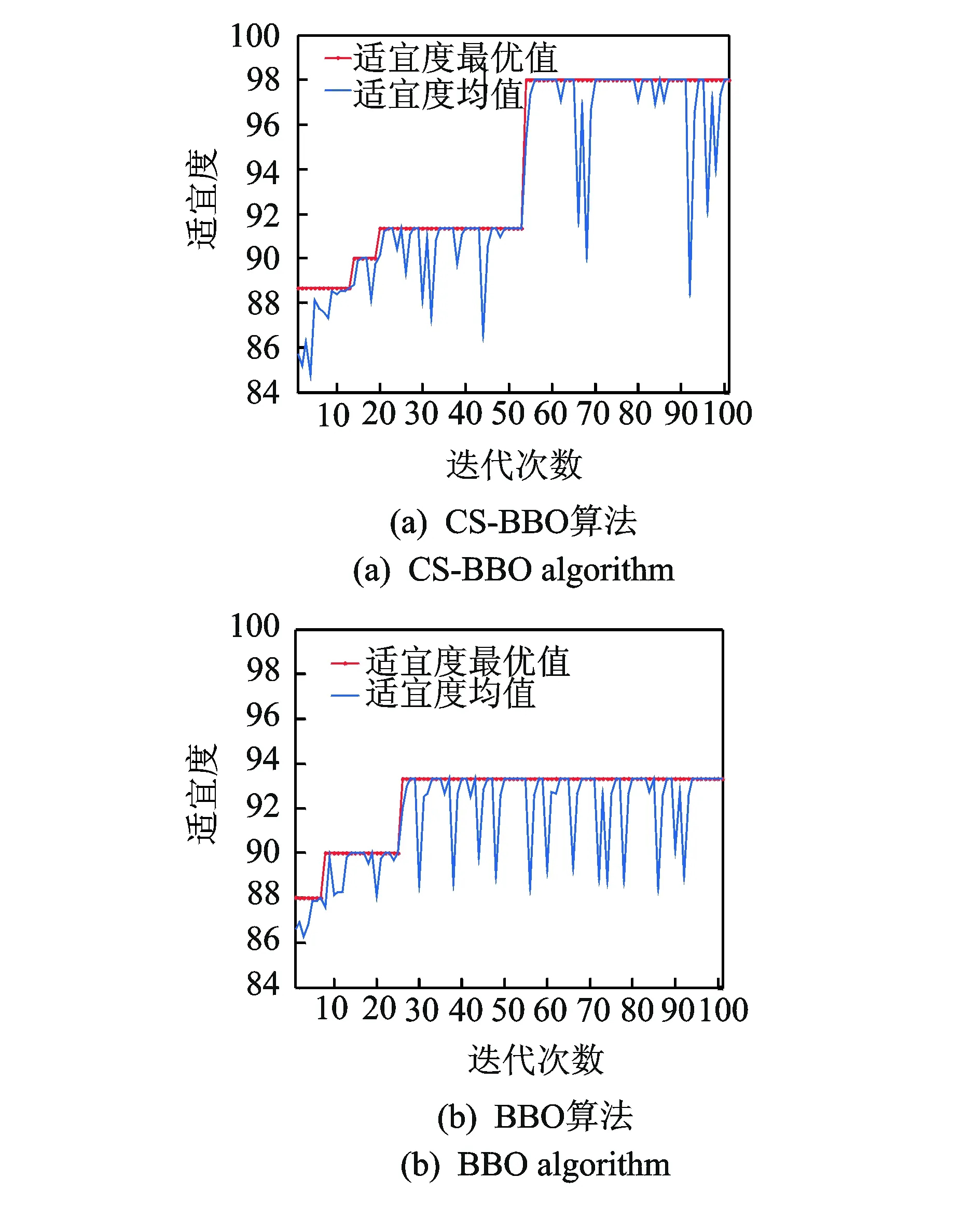
图11 CS-BBO和BBO优化SVM参数的适宜度曲线Fig.11 Fitness curves for CS-BBO and BBO algorithms to optimize SVM parameters process
由图12可知,CS-BBO算法优化SVM诊断模型经过训练后,48组测试样本中,仅有1组样本出现识别错误(转子不平衡故障);而BBO算法优化SVM的诊断模型经48组测试样本测试后,有3组样本出现识别错误(1组正常状态和2组转子不对中故障)。表3为两种算法优化SVM的故障识别统计结果。
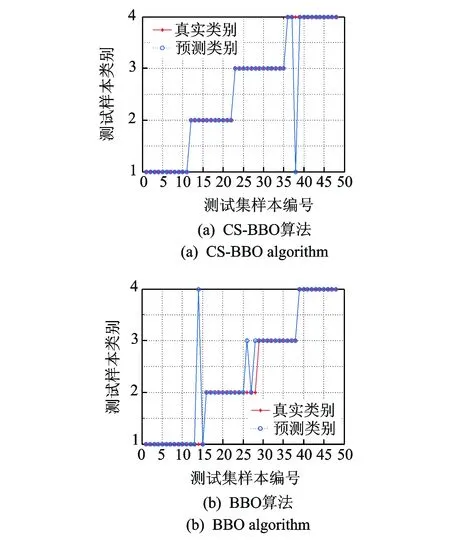
图12 CS-BBO和BBO优化SVM的测试与预测结果对比Fig.12 Comparison of CS-BBO and BBO algorithms to optimize the SVM test and prediction results

表3 两种算法优化SVM故障识别对比结果
由表3可知,在相同试验条件下,与BBO算法优化SVM诊断模型相比,CS-BBO算法优化SVM诊断模型的识别准确率更高,运行时间更短,效率更高,验证了提出的汽轮机转子故障诊断方法的可行性与优越性。
4 结 论
1) 利用混沌理论强大的遍历性与搜索性提高BBO算法的收敛速度和寻优精度。经测试函数验证,CS-BBO算法优于BBO算法。
2) 利用CS-BBO算法获得SVM分类模型的最优参数,提高了SVM的学习能力和泛化能力,获得最佳故障诊断模型。
3) 汽轮机转子故障诊断分析表明,提出的基于CS-BBO算法优化SVM的汽轮机转子故障诊断方法能准确、有效地对汽轮机转子进行故障诊断。在相同条件下,与BBO算法优化SVM方法相比,该方法具有更高的故障诊断准确率与识别效率。
参 考 文 献
[1] 何青,解芳芳,李红,等. 基于流形学习方法的汽轮机组振动特征提取[J]. 振动、测试与诊断, 2014,34(4):705-708.
He Qing, Xie Fangfang, Li Hong, et al. Feature extraction of vibration of turbine unit based on manifold learning method[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(4):705-708.(in Chinese)
[2] Suykens J A K, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999,9(3):293-300.
[3] 赵冲冲,廖明夫,于潇. 基于支持向量机的旋转机械故障诊断[J]. 振动、测试与诊断,2006,26(1):53-57.
Zhao Chongchong, Liao Mingfu, Yu Xiao. Application of support vecter machine to fault diagnosis of rotation machinery[J]. Journal of Vibration, Measurement & Diagnosis, 2006,26(1):53-57.(in Chinese)
[4] 黄慧,顾波. 改进遗传算法在电网规划中的应用[J]. 电力系统保护与控制,2012,40(22):64-67.
Huang Hui, Gu Bo. Application of improved genetic algorithm in the network planning[J]. Power System Protection and Control, 2012,40(22):64-67.(in Chinese)
[5] 朱凤明,樊明龙. 混沌粒子群算法对支持向量机模型参数的优化[J]. 计算机仿真,2010,27(11):183-186.
Zhu Fengming, Fan Minglong. Chaos particle swarm optimization algorithm for optimizing the parameter of SVM[J]. Computer Simulation, 2010,27(11):183-186.(in Chinese)
[6] DAN S. Biogeography-based optimization[J]. IEEE Transactions on Evolutionary Computation, 2008,12(6):702-713.
[7] 丁世飞,齐丙娟,潭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学报,2011,40(1):2-10.
Ding Shifei, Qi Bingjuan, Tan Hongyan. An overview on theory and algorithm of support vector machines[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1):2-10.(in Chinese)
[8] 费胜巍,苗玉彬,刘成良,等. 基于粒子群优化支持向量机的变压器故障诊断[J]. 高电压技术,2009, 35(3):509-513.
Fei Shengwei, Miao Yubin, Liu Chengliang, et al. Fault diagnosis of transformer based on particle swarm optimization-based support vector machine[J]. High Voltage Engineering, 2009, 35(3):509-513.(in Chinese)
[9] 姜久亮,刘文艺,侯玉洁,等. 基于内积延拓LMD及SVM的轴承故障诊断方法研究[J]. 振动与冲击,2016,35(6):104-108.
Jiang Jiuliang, Liu Wenyi, Hou Yujie, et al. Bearing fault diagnosis based on integral waveform extension LMD and SVM[J]. Journal of Vibration and Shock, 2016, 35(6):104-108.(in Chinese)
[10] 李学军,何能胜,何宽芳,等. 基于小波包近似熵和SVM的圆柱滚子轴承诊断[J]. 振动、测试与诊断,2015,35(6):1031-1036.
Li Xuejun, He Nengsheng, He Kuanfang, et al. Cylindrical roller bearing diagnosis based on entropy and support vector wavelet packet approximate machines[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(6):1031-1036.(in Chinese)
[11] 张萍,魏平,于鸿洋,等. 基于混沌的生物地理分布优化算法[J]. 电子科技大学学报,2012, 41(1):65-69.
Zhang Ping, Wei Ping, Yu Hongyang, et al. Biogeography-based optimization algorithm by using chaotic search[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(1):65-69.(in Chinese)
[12] 马海平,李雪,林升东. 生物地理学优化算法的迁移率模型分析[J]. 东南大学学报,2009, 39 (SI):16-21.
Ma Haiping, Li Xue, Lin Shengdong. Analysis of migration rate models for biogeography-based optimization[J]. Journal of Southeast University, 2009, 39 (SI):16-21.(in Chinese)
[13] 范九伦,张雪锋. 分段 Logistic 混沌映射及其性能分析[J]. 电子学报,2009, 37(4):720-725.
Fan Jiulun, Zhang Xuefeng. Piecewise logistic chaotic map and its performance analysis[J]. Acta Electronica Sinica, 2009, 37(4):720-725.(in Chinese)
[14] Shahrzad S, Seyedala M, Andrew L. Biogeography- based optimization with chaos[J]. Neural Comput & Applic, 2014, 25:1077-1097.
[15] 侯新国,刘开培,魏建华. 最佳小波包基改进软阈值的消噪方法及应用[J]. 振动、测试与诊断,2008, 28(4):366-368.
Hou Xinguo, Liu Kaipei, Wei Jianhua. Application of improved soft threshold noise eliminating method based on optimal wavelet packet[J]. Journal of Vibration, Measurement & Diagnosis, 2008, 28(4):366-368.(in Chinese)
[16] Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage[J]. Journal of the American Statistical Association, 1995, 90(432):1200-1224.
[17] 侯平魁,龚云帆,杨毓英,等. 水下目标辐射噪声时间序列的非线性降噪处理[J]. 声学学报,2001, 26(3):207-211.
Hou Pingkui, Gong Yunfan, Yang Yuying, et al. Nonlinear noise reduction of the underwater target radiated noise time series[J]. Acta Acustica, 2001, 26(3):207-211.(in Chinese)
[18] Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5):443-454.
[19] 李琳,张永祥,明廷锋. 改进的LMD方法及其在滚动轴承故障诊断中的应用研究[J]. 振动与冲击,2016, 35(8):183-186.
Li Lin,Zhang Yongxiang,Ming Tingfeng. An improved LMD algorithm and its application in bearing fault diagnosis[J]. Journal of Vibration and Shock, 2016, 35(8):183-186.(in Chinese)
[20] 李志华,曾慧毅,聂超,等. 一种优化迭代权因子的组合代理模型构建方法[J]. 农业机械学报,2016, 47(7):391-397.
Li Zhihua, Zeng Huiyi, Nie Chao, et al. Optimal iterative weight factors method for constructing ensemble of surrogate model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7):391-397.(in Chinese)
[21] Ren Neng, Liang Jun, Gu Bo, et al. Fault diagnosis strategy for incompletely described samples and its application to refrigeration system[J]. Mechanical Systems and Signal Processing, 2008, 22(2):436-450.
