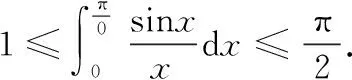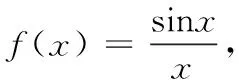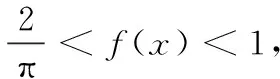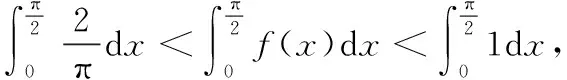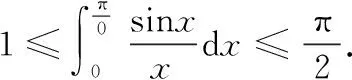微积分思想在不等式证明中的应用
2018-07-17张立欣
◎张立欣 丛 申
(塔里木大学信息工程学院,新疆 阿拉尔 843300)
一、中值定理证明不等式
拉格朗日中值定理:如果函数f(x)满足:
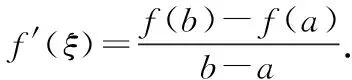
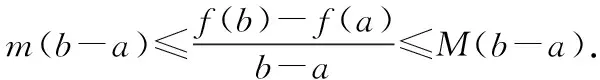


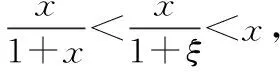
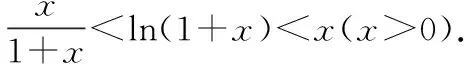
二、单调性证明不等式
函数单调性的判定法:设函数f(x)在开区间I内可导,若f′(x)>0(f′(x)<0),则f(x)在开区间I内单调递增(递减).
若f′(x)>0,则任取x1,x2∈I(x1 若f′(x)<0,则任取x1,x2∈I(x1 要证明f(x)≥g(x),只要证明函数F(x)=f(x)-g(x)的极小值大于0即可. 例3设a>ln2-1为任一常数,试证:当x>0时,x2-2ax+1 证明令f(x)=ex-x2+2ax-1,很明显f(0)=0, 且f′(x)=ex-2x+2a,f″(x)=ex-2, 令f″(x)=0,即x=ln2,则在(0,ln2)内f″(x)<0,在(ln2,+∞)内,f″(x)>0,minf′(x)=f′(ln2)=eln2-2ln2+2a=2-2ln2+2a=2(1-ln2+a)>0, 故f(x)单调递增,因此,f(x)>f(0)=0, 即ex-x2+2ax-1>0,即x2-2ax+1 函数凹凸性的判定法:设函数f(x)在区间I上有二阶导数,若f″(x)>0(f″(x)<0),则f(x)在区间I内图形是凹的(凸的). 证设f(t)=tn,则f″(t)=n(n-1)tn-2>0(t>0), 证f(x)具有二阶导数,由泰勒公式可知: f(x+h)=f(x)+f′(x)h+f″(x)h2+ο(h2), f(x-h)=f(x)-f′(x)h+f″(x)h2+ο(h2). 两式相加可得f(x+h)+f(x-h)=2f(x)+f″(x)h2+ο(h2), 故f″(x)h2+ο(h2)=f(x+h)+f(x-h)-2f(x)≥0. 令h→0,可得f″(x)≥0. 总之,在不等式的证明过程中,结合不等式的特点,恰当运用中值定理、函数的单调性、极值理论、函数的凹凸性、泰勒公式、定积分的性质等,可以将不等式的证明简化,实践证明,这些方法容易被学生理解和接受.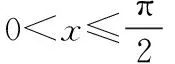
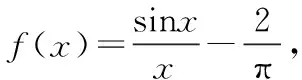
三、极值证明不等式
四、利用函数的凹凸性证明不等式
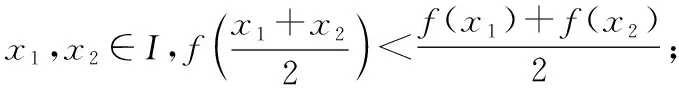

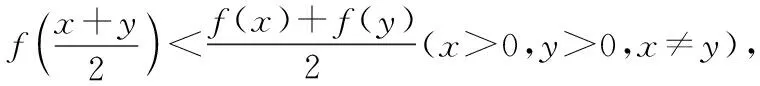
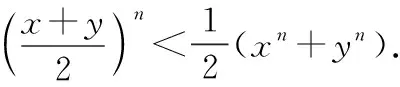
五、泰勒公式证明不等式
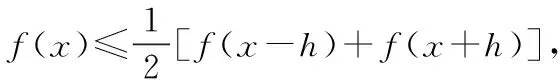
六、定积分证明不等式