有限覆盖定理在若干数学命题证明中的应用①

2015-04-14强华，周虎

佳木斯大学学报（自然科学版） 2015年5期

关键词：开区间银川个数

强华，周虎

(银川能源学院基础部，宁夏银川750105)

0 引言

有限覆盖是数学学科中的一个基础性概念.它涉足数学分析，实分析与泛函分析，拓扑学等数学各领域.

1 有限覆盖、有限覆盖定理

有限覆盖:设S 为直线上的点集，Σ 是一开区间集族(即Σ 的每个元素都是形如(α，β)的开区间).若S 中的任何一点都含在Σ 中至少一个开区间内，则称Σ 为点集S 的一个开覆盖，或者说Σ 覆盖.S 若Σ 中的开区间的个数是无限的，则称Σ 为S的一个无限开覆盖，若Σ 中的开区间的个数是有限的，则称Σ 为S 的一个有限开覆盖.例如，覆盖区间(0，1);

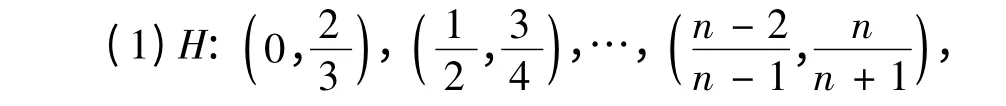
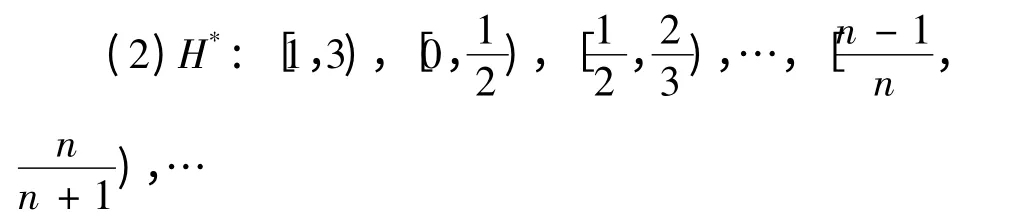
H*是［0，2］的一个无限覆盖，但不是开覆盖，由此也无法产生［0，2］的有限覆盖.

有限覆盖定理(又称Heine－Borel 定理，紧致性定理):若Σ 为闭区间［a，b］的一个开覆盖，则在Σ 中必存在有限个开区间，它们构成［a，b］上的一个开覆盖.(此定理也可以简单地表述为:一个闭区间的任何一个开覆盖中一定有这个闭区间的有限子覆盖.)

此定理说明，实数空间R 的子集A 是一个有界闭集当且仅当A 的每一个开覆盖都有有限子覆盖.

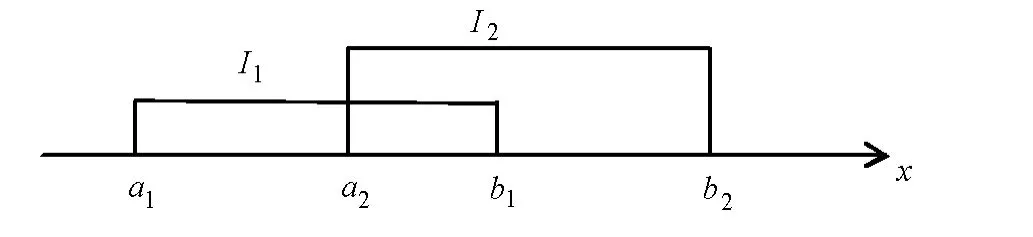
图1

2 有限覆盖定理的应用

有限覆盖定理主要用于对某些数学命题的证明上.

例1 若f(x)在［a，b］上只有第一类不连续点，证明f(x)在［a，b］上有界.

证明取一点x0∈［a，b］，则x0为f(x)的连续点或为第一类不连续点.因此f(x0+0)，f(x0-0)都存在.从而，存在，使，使得当x时，;当x时，

例2 若f(x)在［a，b］上连续，且f(a)·f(b)＜0，则存在c ∈(a，b)，使得f(c)=0.

证明用反证法.假设f(x)在(a，b)内没有零点，由连续函数的保号性，对于任意一点x ∈［a，b］总存在一个邻域U(x)，使得当x ∈U(x)∩［a，b］时，f(x)恒大于零或恒小于零.现让x 取遍［a，b］的值，就得到一个开区间集H={U(x)|x∈［a，b］}.显然，H 为［a，b］上的一个开覆盖.由有限覆盖定理，在H 中含有一个有限个开区间的集合Σ={U(xk)|k=1，2，…，n}覆盖［a，b］，且x1＜x2＜…＜xn，a ∈U(x1)，b ∈U(xn).不妨设f(a)＞0，则由f(x)在U(x1)上的保号性得知，当x ∈U(x1)时，f(x)＞0.取a1∈U(x1)∩U(x2)，则f(a1)＞0.由于f(x)在U(x2)上保号，所以，当x ∈U(x2)时，有f(x)＞0.依此类推得，当x ∈U(xn)时，有f(x)＞0，从而，f(b)＞0.这就与f(a)·f(b)＜0 矛盾.故一定存在c ∈(a，b)，使得f(c)=0.

例3 证明:若一组开区间{In}，In= (an，bn)，n=1，2，…覆盖区间［0，1］.则存在一正数δ，使得［0，1］中任何两点x′，x″，满足|x′-x″|＜δ时，必属于某一区间In.

证明因为区间组{In}覆盖区间［0，1］，由有限覆盖定理，必存在有限个开区间In也覆盖［0，1］，不失一般性，设这组开区间为I1，I2，…，Im.

若I1∩(如图所示).

令J1=(a1，a2)，J2=(a2，b2)，J3=(b1，b2).那么I1，I2，…，Im中只要两个开区间的交非空，就可以产生一串{Jk}.由于I1，I2，…，Im为有限多个，因此{Jk}也是有限个，不妨设J1，…，Js.为再记这些开区间(cn，dn)长为|In|，即|In|=dn-cn.

那么，令δ=min{|I1|，…，|Im|，|J1|，…，|Js|，}则δ ＞0.当x′，x ∈［0，1］且|x′-x″|＜δ 时，显然存在Ik，1 ≤k ≤m，使x′，x″∈Ik.

同理利用有限覆盖定理可证明以下常见数学命题:

(1)若f(x)在［a，b］连续，则f(x)在［a，b］一致连续.

(2)若函数f(x)在［a，b］连续，且∀x ∈［a，b］，有f(x)＞0 则∃r ＞0，∀x ∈［a，b］，有f(x)＞r.

(3)设函数f(x)在［0，+∞)上一致连续，且∀x ＞0，有=0(n 为正整数).则

(4)f(x)是闭区间［a，b］上的函数，满足条件:对每一点x0∈［a，b］，任取ε ＞0，有δ ＞0，对一切x ∈［a，b］∩(x0-δ，x0+δ)，有f(x)＜f(x0)+ε 成立.则:f(x)有最大值.