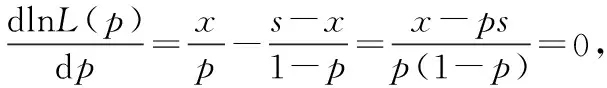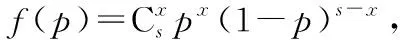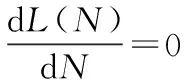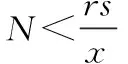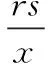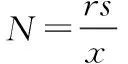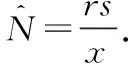一道极大似然估计题的多种解法

◎穆军芬　王志京

(河北工业大学理学院，天津　300401)

极大似然估计(Maximum Likelihood Estimation)法是获得参数估计量的一种广泛使用的方法.极大似然估计量具有许多优良的性质，只要总体分布满足一定的条件，则可证明极大似然估计量具有渐进正态性、渐进有效性、一致性等性质，在一定意义下没有比极大似然估计量更好的估计，所以熟练掌握极大似然估计量的求法是非常重要的.

下面先介绍本文将要用到的知识点.

求极大似然估计的一般步骤[1]：

(1)由总体分布导出样本的联合概率函数(或联合密度函数);

(2)把样本的联合概率函数(或联合密度函数)中的自变量看成已知常数，而把参数θ看作自变量，得到似然函数L(θ);

(3)求似然函数L(θ)的最大值点(常常转化成求lnL(θ)的最大值点)，即θ的极大似然估计量.

极大似然估计的基本思想：求参数的估计量使得实验结果发生的概率最大.

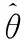
对于初学者来说，若总体分布已知，则已基本掌握了求极大似然估计的一般步骤，但在总体分布未知时，就无法写出似然函数，从而无法用一般步骤去求极大似然估计量.此时，可考虑用极大似然估计的基本思想，极大似然估计不变性等去求极大似然估计量.

本文的目的是通过灵活运用极大似然估计的一般步骤、基本思想及极大似然估计不变性给出一道极大似然估计题的三种解法，以激发学生对相关极大似然估计的解题方法进行探索.

例[3]为了估计池中鱼的数量N，先从池中捞出r条鱼，做记号后再放回池中，再捞出s条鱼，发现其中带记号的鱼有x条，据此求N的极大似然估计量.

从教学过程来看，普遍反映这道题没给出总体的分布，无法写出似然函数，从而无法用一般步骤去求N的极大似然估计量.下面给出该题的三种解法.

解法一设总体

即总体为0-1分布，其概率函数为

P(X=k)=pk(1-p)1-k,k=0,1，0

则从池中随机捞出s条鱼，发现其中带记号的鱼有x条，可看作是从总体X中随机抽取样本容量为s的样本X1,X2,…,Xs,其中这s个样本中有x个取值为1，有s-x个取值为0.

所以似然函数为L(p)=px(1-p)s-x,

从而lnL(p)=xlnp+(s-x)ln(1-p)，

解法二设随机变量

解法三从池中随机捞出s条鱼，发现其中带记号的鱼有x条，这一事件发生的概率为

下面按如下的方法去求L(N)的最大值点：

即L(N)为单增的；

即L(N)为单减的.

在方法一中，需自己寻找总体分布，从而找到似然函数，按求极大似然估计的一般步骤求得概率p的极大似然估计量，再由极大似然估计不变性可得N的极大似然估计.在方法二中，没有找似然函数，而是将事件发生的概率用p表示，由极大似然估计的基本思想求p的极大似然估计量，再由极大似然估计不变性可得N的极大似然估计.在方法三中，直接将事件发生的概率用N表示，由极大似然估计的基本思想求得N的极大似然估计量.在这三个方法中，显然前两个方法相对来说要简单点.

经过探索、尝试后通过一种巧妙的方法完成题目的计算，能够让人体悟到数学的美实在是一种享受，希望借此给读者一点启示.