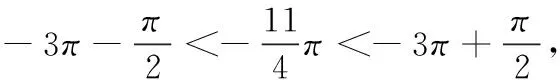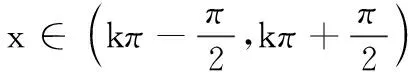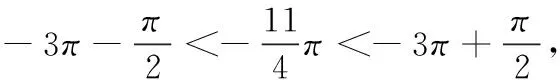一种利用微积分法推广反三角恒等式的方法
2018-07-17马志良
数学学习与研究 2018年13期
◎马志良
(兰州资源环境职业技术学院基础部,甘肃 兰州 730021)
一、反三角恒等式
通常所说的反三角恒等式是指以下四个等式:
arccos(cosx)=x,x∈[0,π];
arccot(cotx)=x,x∈(0,π).
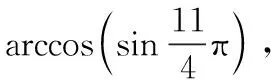
二、反三角恒等式的推广
(一)arcsin(sinx)在一般区间上的恒等式

所以[arcsin(sinx)]′=(-1)k,
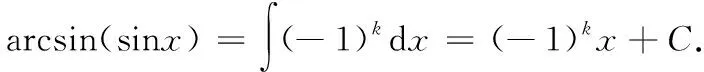
把x=kπ代入上式,可得0=(-1)kkπ+C,
所以C=-(-1)kkπ,
得恒等式arcsin(sinx)=(-1)k(x-kπ).
(二)arccos(cosx)在一般区间[kπ,(k+1)π]上的恒等式
因为x∈[kπ,(k+1)π],
所以[arccos(cosx)]′=(-1)k,
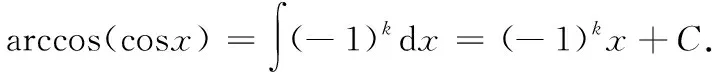
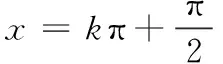

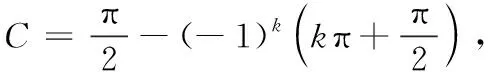
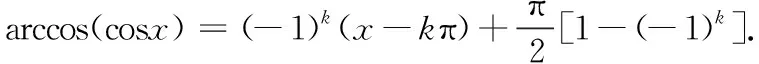
(三)arctan(tanx)在一般区间上的恒等式

把x=kπ代入上式,可得0=kπ+C,所以C=-kπ,
得恒等式arctan(tanx)=x-kπ.
(四)arccot(cotx)在一般区间(kπ,(k+1)π)上的恒等式

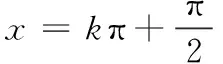
所以C=-kπ,
得恒等式arccot(cotx)=x-kπ.
(五)arccos(sinx)在一般区间上的恒等式

所以[arccos(sinx)]′=(-1)k+1,


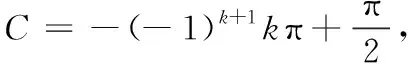

(六)arcsin(cosx)在一般区间[kπ,(k+1)π]上的恒等式
因为x∈[kπ,(k+1)π],
所以[arcsin(cosx)]′=(-1)k+1,

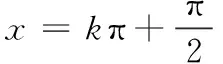
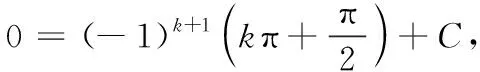
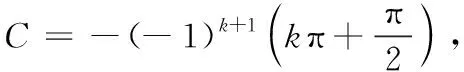
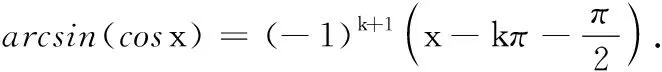
(七)arccot(tanx)在一般区间上的恒等式
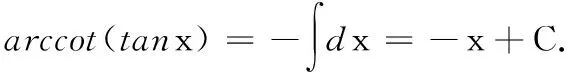
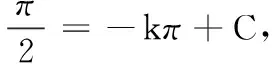
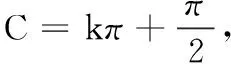
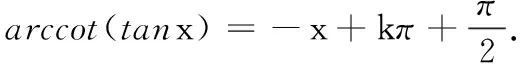
(八)arctan(cotx)在一般区间(kπ,(k+1)π)上的恒等式
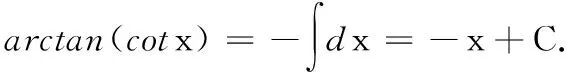
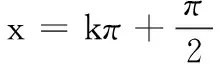
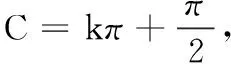
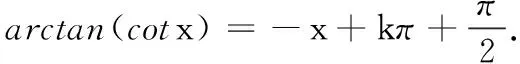
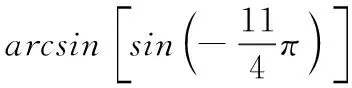
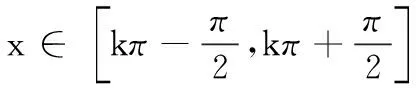
arcsin(sinx)=(-1)k(x-kπ).