带转运环节运输问题的数学模型

◎肖庆丰　冯天祥

(东莞职业技术学院公共教学部，广东　东莞　523808)

带有转运环节的运输问题要比通常的运输问题复杂，在物流运筹学中通常用表上作业法来实现其求解过程[1-2]，也有学者编写算法利用计算机实现其求解过程[3]，而这些求解过程对物流专业的师生来说都不易理解和难以求解，寻找一种易于理解，求解便利的方法也就成为当务之急.我们将这种带有转运环节的运输问题转化为一般运输问题，再给出相应的线性规划模型，最后对模型进行推广.

一、带有转运环节运输问题的一般形式

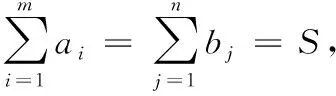
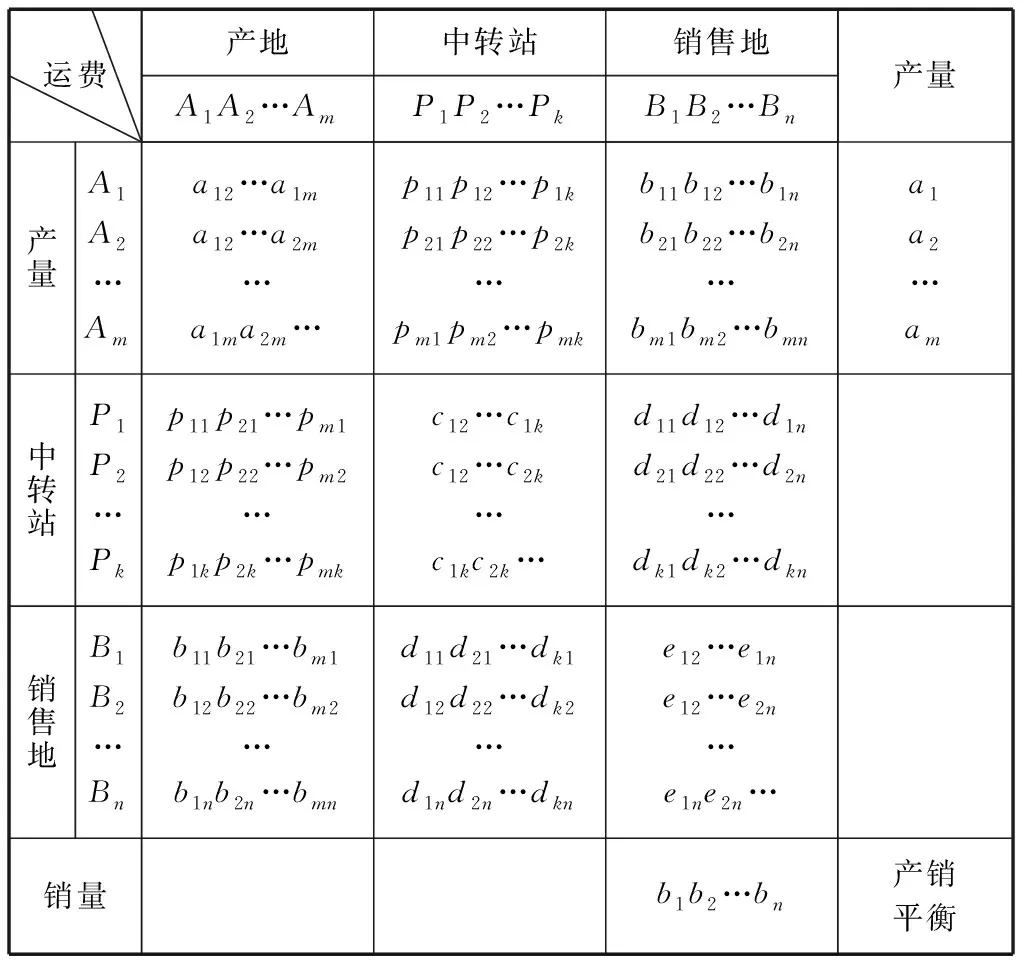
表1

由表1可见，从A1直接到B2的运费为b12；A1→A2→B2的运费为a12+b22；如果是A1→P2→B2，运费为p12+d22；等等.可见有中转运输的情况远远比一般的运输问题复杂，有必要进行适当的技术处理.首先考虑将上述问题转化为一般运输问题，以此为基础建立相应的线性规划模型，然后推广这一问题.

二、将带有转运环节运输平衡问题转化为一般运输平衡问题的步骤

第一步：把问题所涉及的所有产地、销地和中转站都看成既是产地也是销售地，于是原问题就变成一个有m+k+n个产地、m+k+n个销售地的运输系统.

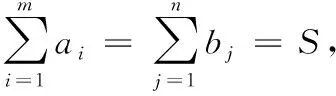
第三步：在新的运输系统中，用xij表示第i个产地运输到第j个销售地的物资数量(i，j=1，2，…，m+k+n)，其中的xii是一个虚拟变量，其对应运费为0，它的实际意义就是自己运输给自己的物资数量，S-xii就是每个中转站的实际转运量.

第四步：在新的运输系统中，原有的产地和销售地也具有转运的功能，所以在原有产量和销量的基础上应增加S.也就是说，产地A1，A2，…，Am的产量分别为a1+S，a2+S，…，am+S.

销量都是S；销售地B1，B2，…，Bn的销量分别是b1+S，b2+S，…，bn+S，产量都是S.

由此我们将原问题转化为如下产销平衡的新运输问题，产地的产量、各销售地的销量及各地的运费等数据见表2.

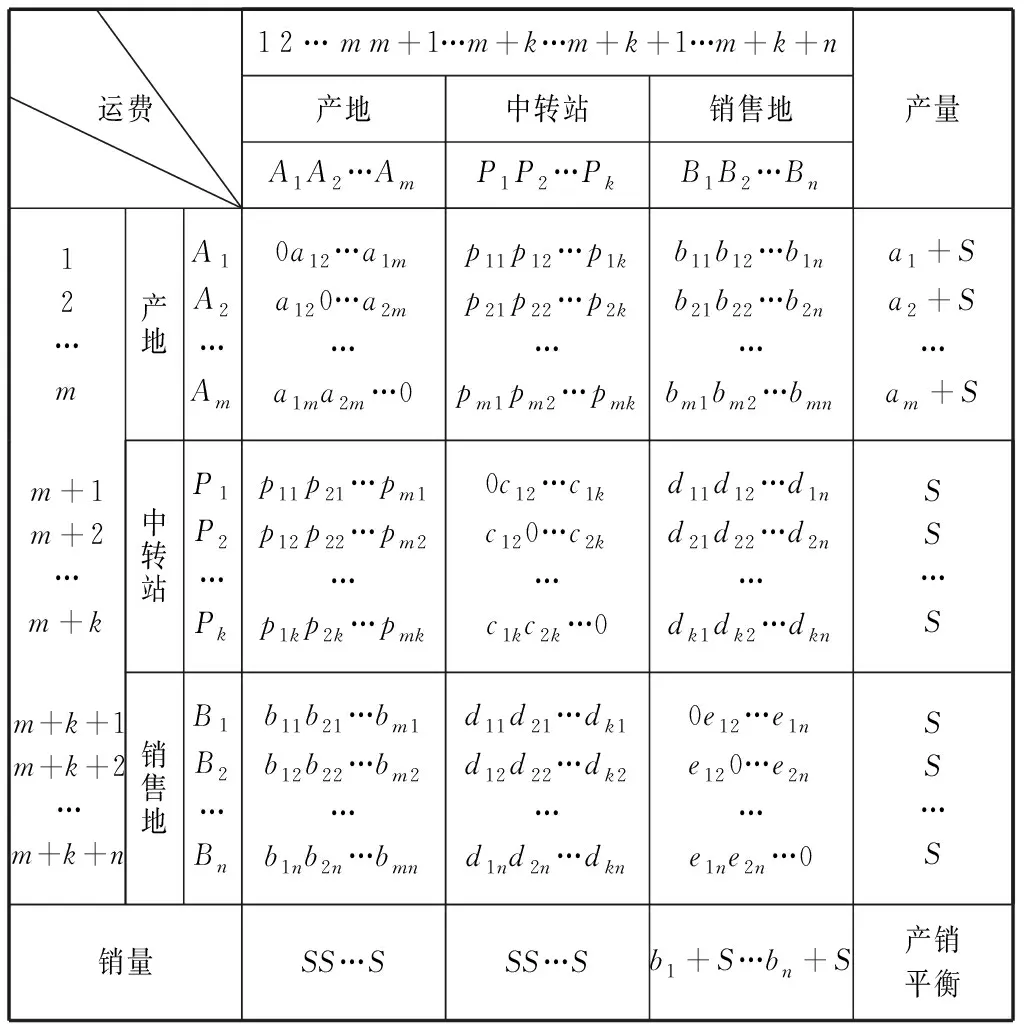
表2

三、数学模型的建立

与通常的运输问题一样，目标为求函数z的最小值，其中

产量约束条件是

销量约束条件是

变量非负约束：xij≥0(i，j=1，2，…，m+k+n).

于是可建立如下线性规划模型：

四、模型的推广

带转运环节的运输模型还可从如下几个方面进行推广：

1.如果从产地Ai不能直接到达销地Bj，需要通过中转站进行中转，就取相应的运费bij为充分大的整数M，然后在目标函数z中用M替换元素bij即可.

2.如果产销不平衡，就分两种情况进行处理