一类不定积分的计算方法与技巧

◎史和娣

(江苏农林职业技术学院基础部，江苏　镇江　212400)

一、引 言

不定积分与微分(或导数)是逆运算的关系，我们学习者往往在从导数到不定积分的过渡时，会遇到一些理解上的困难.而不定积分也是整个微积分学的重要内容之一，也是计算定积分的基础.熟练掌握不定积分的计算方法是学好积分的必备条件，同时不定积分的计算对思维的训练以及后续知识的学习也起着重要的作用.本文主要通过一类常见的被积函数是多项式之比的不定积分展开讨论，帮助学生熟练掌握不定积分的计算方法和技巧，促使学生更好地灵活运用不定积分的计算方法处理积分问题.

二、不定积分的计算

1.当n=1，n≥m时，即分母是一次多项式，不妨设为Pn(x)=ax+b(a≠0)，且分子最高次数比分母小.

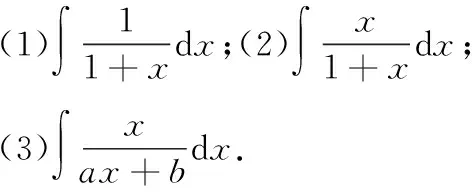
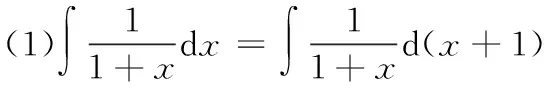
=ln|x+1|+C(凑微分法)；

=x-ln|x+1|+C(恒等变形、凑微分法)；

2.当n=2，n≥m时，即分母是二次多项式，不妨设为Pn(x)=ax2+bx+c(a≠0)，且分子次数比分母小.

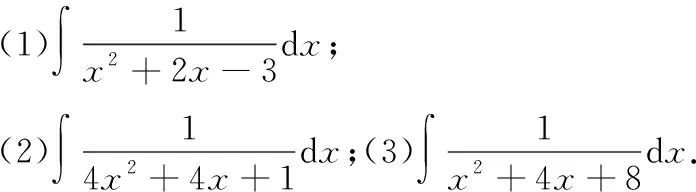
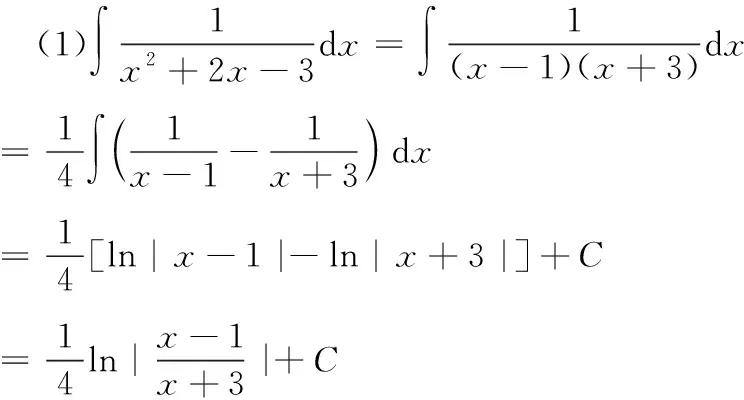
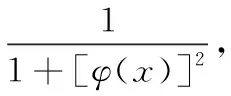
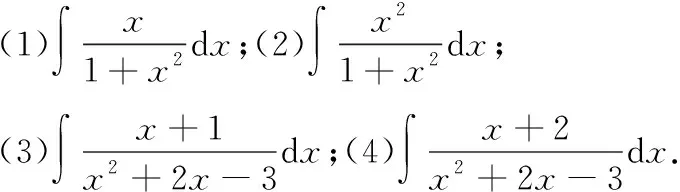
=x-arctanx+C；

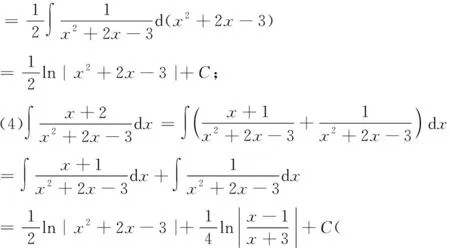
3.当1≤n≤m时，即分子最高次数比分母大.

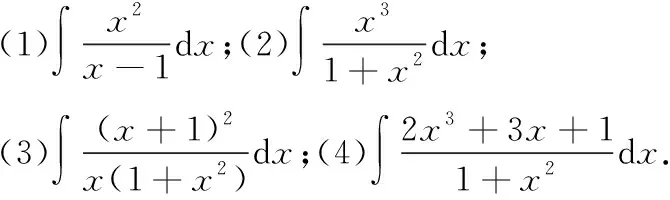
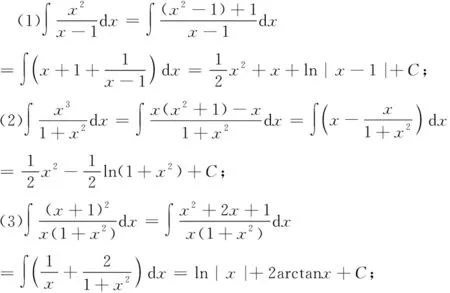
除数x2+1被除数2x3+3x+1商2x2x3+2xx+1余数

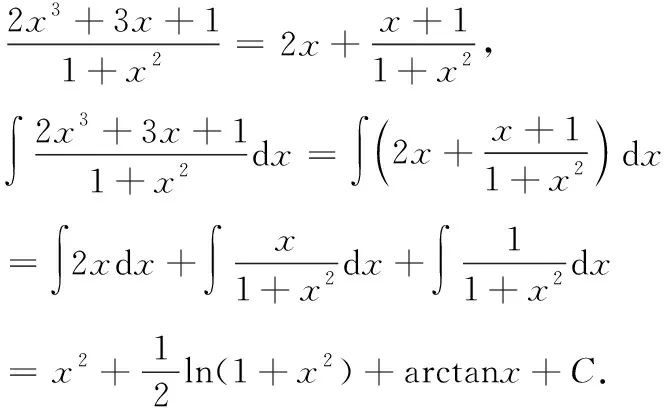
通过以上例题的解答，可以发现被积函数稍微改变一点，积分方法可能完全不同，因此，在学习过程中，一定要注意比较，几种积分方法灵活使用.