罗尔定理中辅助函数的构造法
2022-12-01郭元春陈思源马晓燕
郭元春 陈思源 马晓燕
1.西安思源学院基础部 陕西西安 710038;2.西安思源学院高等教育营销研究中心 陕西西安 710038
微分中值定理在微积分学中占有十分重要的地位,是用函数局部性质推断整体性质的有力工具。罗尔定理是微分中值定理中最为基础的一个,定理内容:若函数f(x)满足在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则存在某个中值ξ∈(a,b),使得等式f′(ξ)=0。利用罗尔定理证明中值等式问题的难点就是辅助函数的构造。刘文武、张军、肖俊等人[1-3]采用逆向思维法对该类问题做了相应的研究。逆向思维法是从结果出发分析中值等式的特点,选择适当的方法构造辅助函数。
微分中值等式问题常见的形式是:已知函数f(x)满足在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(x)满足某些附加条件,求证存在某个中值ξ∈(a,b),使得等式F(ξ,f(ξ),f′(ξ))=0。该等式左边看作是某个函数g(x)在点ξ处的导数,即g′(ξ)=0。由拉格朗日中值定理可知,g(x)=C是满足该等式的最简单的函数。显然这个隐函数是原微分方程的通解,因此,在微分中值问题中,一般把通解中的积分常数令为辅助函数。本文采用逆向思维法,对微分中值问题中构造辅助函数的常见题型作归纳和总结。
一、利用分离变量法构造辅助函数
(一)证明的等式是关于ξ,f(ξ),f′(ξ)的微分方程
例1[4]:设函数f(x)在闭区间[0,π]上连续,在开区间(0,π)内可导,证明:在开区间(0,π)内至少存在一点ξ,使得f′(ξ)sinξ=-f(ξ)cosξ。
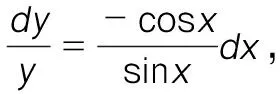
证明:令F(x)=f(x)sinx,显然,F(x)在闭区间[0,π]上连续,在开区间(0,π)内可导,且F(0)=F(π),故由罗尔定理知,在开区间(0,π)内至少存在一点ξ,使得F′(ξ)=0,而F′(ξ)=f′(ξ)sinξ+f(ξ)cosξ,也就是说,在开区间(0,π)内至少存在一点ξ,使得f′(ξ)sinξ=-f(ξ)cosξ。

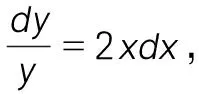
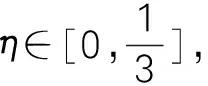
显然,F(x)在闭区间[η,1]⊂[0,1]上连续,在开区间(η,1)⊂(0,1)内可导,且F(η)=e-η2f(η),F(1)=e-1f(1),即F(η)=F(1),由罗尔定理知,在开区间(η,1)⊂(0,1)内至少存在一点ξ,使得F′(ξ)=0。
又F′(ξ)=-2ξe-ξ2f(ξ)+e-ξ2f′(ξ)=e-ξ2[f′(ξ)-2ξf(ξ)],且e-ξ2≠0,故f′(ξ)-2ξf(ξ)=0。也就是说,在开区间(0,π)内至少存在一点ξ,使得f′(ξ)sinξ=-f(ξ)cosξ。
(二)证明的等式是关于f(ξ),f′(ξ),g(ξ),g′(ξ)的微分方程
例2[5]:设f(x)和g(x)在上[a,b]连续,在(a,b)内可导,且f(a)=f(b)=0,g(x)≠0证明在(a,b)内至少存在一点ξ使得f′(ξ)g(ξ)+2f(ξ)g′(ξ)=0。
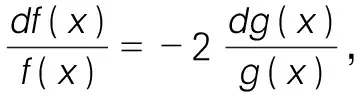
证明:令F(x)=f(x)g2(x),显然,F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且F(a)=F(b),故由罗尔定理知,在开区间(a,b)内至少存在一点ξ,使得F′(ξ)=0,而F′(ξ)=g(ξ)[f′(ξ)g(ξ)+2f(ξ)g′(ξ)],又g(x)≠0,故在开区间(0,π)内至少存在一点ξ,使得f′(ξ)g(ξ)+2f(ξ)g′(ξ)=0。
应用实例:若函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,并且f(0)=0,如果x∈(0,1),f(x)≠0,证明在(0,1)内至少存在一点ξ使得f′(ξ)f(1-ξ)=f(ξ)f′(1-ξ)。
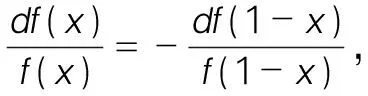
二、利用一阶线性方程的通解构造辅助函数
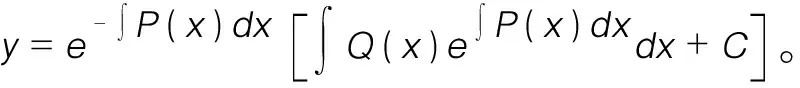
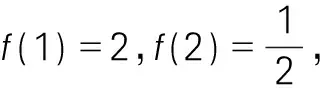
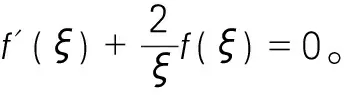
应用实例:设f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b)=0,则在(a,b)内至少存在一点ξ,使得2f(ξ)=f′(ξ)。
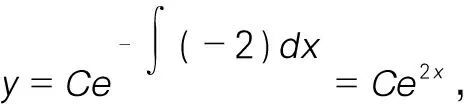
证明:令F(x)=e-2xf(x),显然,F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且F(a)=F(b)=0,故由罗尔定理知,在开区间(a,b)内至少存在一点ξ,使得F′(ξ)=0,而F′(ξ)=-2e-2ξf(ξ)+e-2ξf′(ξ)=e-2ξ[-2f(ξ)+f′(ξ)],又e-2ξ≠0,故在(a,b)内至少存在一点ξ,使得2f(ξ)=f′(ξ)。
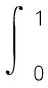
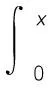
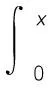
例5:若函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,且f(0)=f(1)=2,证明在(0,1)内至少存在一点ξ使得f′(ξ)+f(ξ)=2。
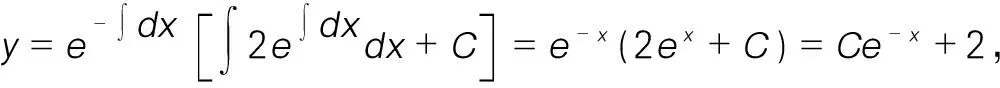
证明:令F(x)=ex[f(x)-2],F(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,且F(0)=F(1)=0,故由罗尔定理知,在开区间(0,1)内至少存在一点ξ,使得F′(ξ)=0。而F′(ξ)=eξ[f(ξ)-2]+eξf′(ξ)=eξ[f(ξ)+f′(ξ)-2],又eξ≠0,故在(0,1)内至少存在一点ξ,使得f′(ξ)+f(ξ)=2。
在利用一阶线性方程的通解公式构造辅助函数时,一定要仔细观察中值等式的特点,找到P(x),Q(x),求出通解。
三、利用降阶的思想构造辅助函数
(一)利用可降阶方程降阶一次后得到的解构造辅助函数
形如y″=f(x,y′)的方程称为不显含y的可降阶微分方程[6],该方程的特点是方程中同时含有y′,y″,且不显含y。在计算时可令y′=p(x),则y″=p′(x),原方程可化为一阶方程p′=f(x,p),利用分离变量法或一阶线性齐次方程的通解公式可得φ(x,p)=C,从而可构造出辅助函数。
例6:设函数f(x)在[0,1]上二阶连续可导,且f(0)=f(1)=2,证明:至少有一点ξ∈(0,1),使得2f′(ξ)+ξf″(ξ)=0。
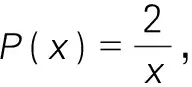
证明:由于函数f(x)在[0,1]上二阶连续可导,故f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,并且f(0)=f(1)=2,故由罗尔定理知,至少存在一点η∈(0,1),使得f′(η)=0。对F(x)=x2f′(x),在[0,η]上连续,在(0,η)内可导,且F(0)=F(η)=0,再次利用罗尔定理,可证至少有一点ξ∈(0,η)⊂(0,1),使得2f′(ξ)+ξf″(ξ)=0。
(二)利用分部积分法构造辅助函数
例7 设f(x)和g(x)在上[a,b]连续,在(a,b)内可导,在(a,b)内g(x)≠0,g″(x)≠0,且f(a)=f(b)=g(a)=g(b)=0,证明在(a,b)内至少存在一点ξ使得f″(ξ)g(ξ)-f(ξ)g″(ξ)=0。
分析:该微分中值等式属于二阶微分方程,但只含有两个函数的二阶导数f″(x),g″(x),不含f′(x),g′(x),为了使用降阶的思想
f″(x)g(x)=f(x)g″(x)
两边同时对x积分,得:
证明 令F(x)=f′(x)g(x)-f(x)g′(x),显然,F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且F(a)=F(b)=0,故由罗尔定理知,在开区间(a,b)内至少存在一点ξ,使得F′(ξ)=0,而F′(ξ)=f″(ξ)g(ξ)-f(ξ)g″(ξ),故在(a,b)内至少存在一点ξ,使得f″(ξ)g(ξ)-f(ξ)g″(ξ)=0。
以上分析了罗尔定理证明微分中值等式问题的几个典型例题,都是从导数和积分的互逆性出发,通过微分方程求解的方法或不定积分法等逆向思维法构造辅助函数。在平常的教学过程中,可以借助此类题型提高学生的逻辑思维能力和逆向思维能力,逐步培养学生综合应用微积分知识解决实际问题的能力。
