一道数学综合题的思考之路

（江苏省淮阴中学开明校区）

近日，笔者所在的江苏省淮阴中学教育集团进行了一场九年级阶段性测试，作为数学阅卷负责人，笔者对试卷的最后一道压轴题思考颇多，现将思考过程与各位同仁交流如下.

一、题目再现

题目如图1，在△ABC中，AB=5，AC=9，动点P从点A出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从点C出发，以相同的速度在线段AC上由C向A运动，当点Q运动到点A时，点P，Q同时停止运动.以PQ为边作正方形PQEF（点P，Q，E，F按逆时针排序），以CQ为边在AC上方作正方形QCGH，设点P运动的时间为t．

（1）求tanA的值；

（2）当△APQ为等腰三角形时，求t的值；

（3）当t为何值时，正方形PQEF的顶点F落在正方形QCGH的边上，直接写出t的值.

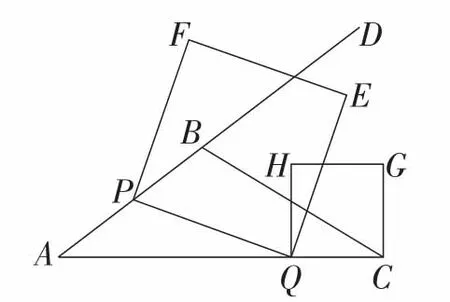
图1

题目提供的参考答案非常简洁，第（1）（2）小题自然无需研究，关键是第（3）小题，答案是怎么得到的？

二、解决问题

凭借几何画板软件的演示效果，以及空间想象，我们确定点F落在正方形QCGH的边上只有两种情况.

情况1：如图2，当点F落在边HG上时，

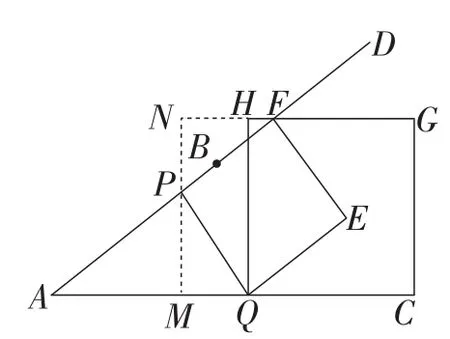
图2

作PM⊥AC于点M，交GH的延长线于点N.

因为AP=CQ=5t，

所以PM=3t，AM=4t.

则MQ=9-9t.

由△PMQ≌△FNP，

得PN=9-9t.

因为MN=HQ=QC，

所以9-9t+3t=5t.

解得

情况2：如图3，当点F落在边GC上时，

作PM⊥AC于点M，过点P作TN⊥GC于点N.

因为AP=CQ=5t，

所以PM=3t，AM=4t.

则QM=9t-9.

由△QTP≌△PNF，

得PN=PM=3t.

因为TN=QC，

所以9t-9+3t=5t.

解得

因为

所以

上述问题似乎得到圆满解决，可是仔细想想，问题很多.

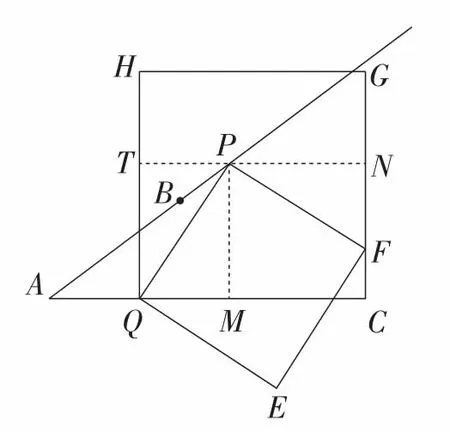
图3

三、思考之路

1.如何分类

因为正方形QCGH有4条边，所以点F落在正方形QCGH的边上应该分为四类：点F落在边QH上；点F落在边HG上；点F落在边GC上；点F落在边CQ上.另外两类为什么不考虑？学生在考试中不能利用几何画板软件，空间想象力又达不到，该怎么办？当然，计算是最有说服力的方法.

情况3：如图4，当点F落在边QH上时，作PM⊥AC于点M.

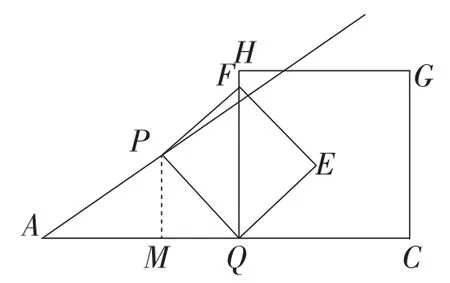
图4

因为AP=CQ=5t，

所以PM=3t，AM=4t.

则QM=9-9t.

由△PMQ是等腰直角三角形，得

PM=MQ.

所以9-9t=3t.

解得

情况4：如图5，当点F落在边AC上时，作PM⊥AC于点M.

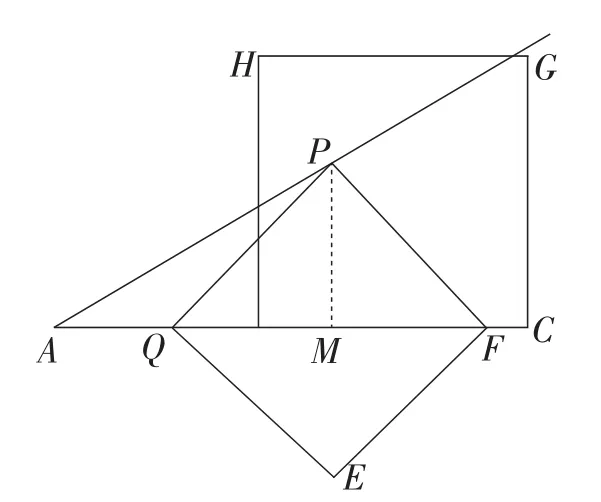
图5

因为AP=CQ=5t，

所以PM=3t，AM=4t.

则QM=9t-9.

由△PMQ是等腰直角三角形，

得PM=MQ.

所以9t-9=3t.

2.如何画图

事实上，上述图形比较难画，这也是学生解题时遇到的最大困难.若先在∠A的两边上取AP=CQ，确定点P，Q的位置，再画出正方形PQEF，此时的点F很难恰巧就在正方形QHGC的边上，要么将就，要么就通过不断调整点P，Q的位置来达到要求.可是即便如此，点F落在边QH上和边CQ上还是画不好，因为根本不可能.

怎样才能既快又好地画出体现题意的图形呢？分析发现：此题画图的关键是画出两个正方形的相对位置，而AP与CQ虽然相等，但是不画相等不影响解题.于是可以采用逆向画图的方法：（1）先画出正方形QHGC；（2）在正方形的一条边上取一点F；（3）以FQ为对角线画正方形QPFE；（4）最后画∠CAP.

下面以图4为例分步画图，如图6所示.

图6

这样的图形基本上准确地表达了题意（除了AP，CQ不相等外），更方便了计算.

3.如何取舍

研究不存在的两解如何舍去，也就自然涉及到另外两解为什么合理.

图2中，当时，所以NH＜NF＜NG，即点F在边HG上.

图4中，当时，FQ=6t，HQ=5t.因为6t＞5t，所以FQ＞HQ，即点F不在边HQ上.

图5中，当时，FQ=6t，QC=5t.因为6t＞5t，所以QF＞QC，即点F不在边QC上.

综上可得，是不符合题意的.同时这一过程也让我们进一步发现，情况1和情况2必须通过计算、比较，才能判断点F一定在边HG，GC上.情况3和情况4无需计算t的值，只要通过比较，就可以判断点F不可能在边HQ，QC上.

4.还可以如何计算

考虑到此题4种情况画图难度大，且需要进行比较、取舍，联想到平面直角坐标系，此题可以通过建立平面直角坐标系来解决问题.

以点A为原点，AC所在直线为x轴，建立平面直角坐标系.

当点P，Q所在直线垂直于x轴时，因为AM+CQ=9，所以4t+5t=9.解得t=1.

① 当0＜t≤1时，如图7，作PM⊥AC于点M，作FN⊥MP交MP的延长线于点N.

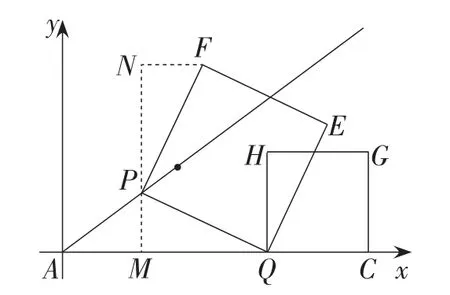
图7

因为AP=CQ=5t，

所以PM=3t，AM=4t.

则MQ=9-9t.

由△PMQ≌△FNP，

得NP=9-9t，NM=9-9t+3t=9-6t.

此时N(4t，9-6t)，F(7t，9-6t).

若点F落在QH上，

则点F，H的横坐标相等，

所以7t=9-5t.

解得

此时，点F的纵坐标为点H的纵坐标为

因为

所以点F不在边QH上.

若点F落在HG上，

因为点F，H的纵坐标相等，

所以5t=9-6t.解得

此时，点F的横坐标为点H的横坐标为点G的横坐标为9.

因为

所以点F在边HG上.

②当时，如图8，作PM⊥AC于点M，作PN⊥PM交PM的平行线GC于点N.

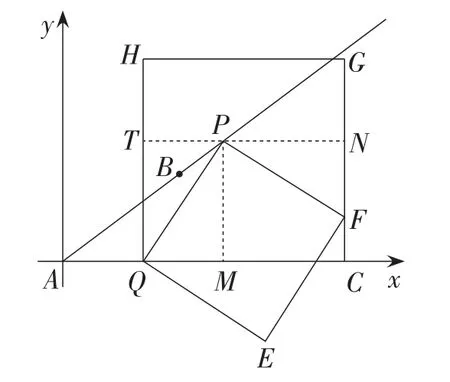
图8

因为AP=CQ=5t，所以PM=3t，AM=4t.

则MQ=9t-9.

由△PMQ≌△PNF，

得PN=3t，NF=9t-9.

此时N(7t，3t)，F(7t，9-6t).（这时发现点F的坐标表达式不变.）

若点F落在GC上，

因为点F，C的横坐标相等，

所以

此时，点F的纵坐标为点G的纵坐标为

因为

所以点F在边GC上.

若点F落在CQ上，因为点F，C的纵坐标相等，

所以

此时，点F的横坐标为点C的横坐标为9.

因为

所以点F不在边CQ上.

综上可得

四、解题感悟

1.分类是方向

关于分类，《义务教育数学课程标准（2011年版）》中指出，分类是一种重要的数学思想，在研究数学问题的过程中，常常需要通过分类讨论解决问题，分类的过程就是对事物共性的抽象过程.教学活动中，要使学生逐步体会为什么要分类，如何分类，如何确定分类的标准……

此题是由点P，Q的运动而产生不同的情况，因此，必须考虑动点运动的全过程，即以点F落在正方形QCGH的哪一条边上作为分类标准，分成四类，这是解题的大方向.至于几何画板软件的演示，它虽然能够帮助我们直观地看到动点的运动过程（即符合条件的点只有两类），但是也只能在教师讲解时帮助学生理解，在实际解题中学生是无法想象出来的.

2.画图是关键

数与形是数学中两个最古老也是最基本的研究对象，数形结合思想包括以数解形、以形助数两个方面.此题如果没有图形，求点P运动的时间（数）将无法进行，快速画出能够恰当表达题意的图形是解题的关键.此题的四个图形中有两个符合题意，画起来较容易，而另外两种原本就不存在，如果按照图形的形成顺序画，就很难画出顶点F落在正方形QCGH相关边上的正方形，即使勉强画出也会因图形变形而使计算陷入困境.逆向画图的方法成功解决了这一困难，至于图中AP，CQ长度不等对解题几乎没有影响.

3.计算是核心

这里说的计算不仅仅是一般意义上根据法则和运算律的运算，而是结合图形，构造模型、思路可行的综合思维过程，准确的计算结果是数学综合能力的展现，也是题目的核心.此题图2、图3两种情况的计算过程中紧扣正方形的特征构造基本图形“一线三等角”，列方程解决问题，而图7、图8通过建系，不追求形的到位，通过不同位置的坐标特征来解决问题，这也正是数形结合的另一方面“以数解形”的具体体现.

4.取舍是点睛

准确的计算是核心，答案的取舍可谓点睛之笔，是完美解题的收官动作.此题答案的取舍，可以通过符合题意的画图进行，但心中难免忐忑.一般综合题的答案取舍往往由动点运动的时间范围来确定，但是此题例外，所有答案均在时间范围内.通过对计算过程的进一步分析发现，得出答案的过程都抓住了点运动的一个维度（横或竖），因此必须检验另一个维度是否满足，建系方法的灵感也就来源于这一检验要求，点睛之笔使结果更加完美，也使解题过程更加丰富.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.