读《篱笆怎么围面积最大》的思考

（湖北省孝感市文昌中学）

问题有一堵长为12m的墙，利用这堵墙和长为60m的篱笆围成一个矩形养鸡场，怎样围面积最大？最大面积是多少？

这是由人教版《义务教育教科书·数学》九年级上册（以下统称“教材”）的内容演变而来的一道题.祝立新老师在2017年《中国数学教育》（初中版）第3期《篱笆怎么围面积最大》一文中，从四个不同的位置情形入手，进行了非常详尽的讨论分析，并且做了引申和拓展，读后很受启发.笔者在受益匪浅之余，也进行了一些思考.

思考1：问题中“利用这堵墙”的含义，整体上看可分为“一边靠墙”和“一边包含墙”两种情形.至于教材中的图4，通过平移矩形，完全可以转化为前面的两种情形之一.下面，我们分两种情况讨论如下.

（1）若一边靠墙，如图1，同祝老师的分析，得到当AB=12m，养鸡场面积最大为288m2；

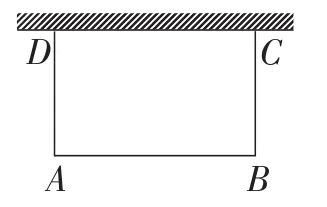
图1

（2）若一边包含着墙，如图2所示.从整体上看，墙可以看成是边DC上运动的“线段”，边长与墙长的差即为矩形这一边所用的篱笆长.

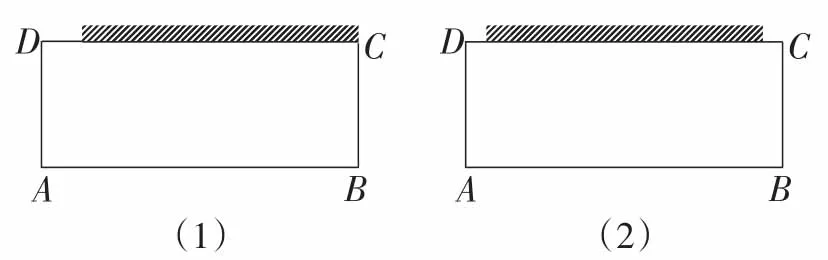
图2

设AB=xm，

则AD+x+BC+(x-12)=60.

所以AD=BC=(36-x) m.

所以S矩形ABCD=x(36-x)=-(x-18)2+324.

因为-1＜0，

所以当x=18时，S矩形ABCD有最大值324.

综上归纳，可得当矩形的长和宽都是18m时，养鸡场面积最大，最大面积是324 m2.

思考2：上述结论中，养鸡场面积最大时，所建矩形的“一边包含墙”，并且其形状正好是一个正方形.联想到“周长一定的所有矩形中，正方形的面积最大”，于是闪现出一个整体思想新解法.

解：把这堵墙看成一段特殊的篱笆，

则共有篱笆72m.

设这些篱笆围成的矩形的一边长为xm，

则矩形的另一边长为(36-x) m.

所以S矩形ABCD=x(36-x)=-(x-18)2+324.

因为-1＜0，

所以当x=18时，S矩形ABCD有最大值324，此时矩形为边长等于18的正方形.

因为18＞12，

所以这堵墙可以成为上述正方形一边上的一部分.

所以以这堵墙为基础，围建成边长为18m的正方形，便得到了符合题意的面积最大的养鸡场.

思考3：上面运用数学整体思想方法，算“总账”，巧转化，避免了局部分析过程中的分类讨论之“繁”，简洁明了，并且还原了问题内含的本质.运用这种整体转化思想方法解决祝老师文中的拓展问题，也可以使得其过程简化.

拓展1：有一堵长为am的墙，利用这堵墙和长为60m的篱笆围成一个矩形养鸡场，怎样围面积最大，最大面积是多少？

解析：先把这堵墙看成一段特殊的篱笆，

则共有篱笆(a+60) m.

同上面的研究方法得到当这些篱笆围成边长为的正方形时，其面积最大.

再分类讨论如下.

（1）若即当a≤20时，同上，以这堵墙为基础，围建成边长为的正方形，便得到了符合题意的面积最大的养鸡场.

此时养鸡场最大面积为

（2）若即当a＞20时，由于“墙”不能弯曲，所以上述正方形无法围成，于是问题转化为矩形“一边靠墙”类型问题.

同图1，设AB=xm，

则

所以

再分类讨论如下.

①如果20＜a＜30，则0＜x≤a.

函数在此区间单调递增，

所以当x=a时，此时矩形两邻边长分别为am，养鸡场最大面积为

②如果a≥30，因为

所以当x=30时，S矩形ABCD有最大值450，此时矩形的长为30m，宽为15m，养鸡场最大面积是450 m2.

思考4：如果这堵墙的长度不变，而篱笆长是一个变数，情况又怎么样？我们进行另一个层面的拓展如下.

拓展2：有一堵长为12m的墙，利用这堵墙和长为am的篱笆围成一个矩形养鸡场，怎样围面积最大，最大面积是多少？

解析：先把这堵墙看成一段特殊的篱笆，则共有篱笆(a+12)m.

同上面的研究方法得到当这些篱笆围成边长为的正方形时，其面积最大.

再分类讨论如下.

（1）若即当a≥36时，同上分析，以这堵墙为基础，围建成边长为的正方形，便得到了符合题意的面积最大的养鸡场.此时养鸡场最大面积为

（2）若即当a＜36时，同上，问题转化为矩形“一边靠墙”类问题.

如图1，设AB=x，

则

所以

再分类讨论如下.

①如果则24＜a＜36.

因为0＜x≤12，

所以函数在此区间单调递增.

所以当x=12时，矩形ABCD的面积有最大值，最大值为

此时矩形两邻边长分别为12 m，养鸡场最大面积为(6a-72) m2.

②如果即0＜a≤24.

因为

所以当时，S矩形ABCD有最大值此时矩形的长为宽为养鸡场最大面积是

思考5：如果这堵墙呈“L”形，又将会出现什么情况？看下面的拓展.

拓展3：如图3，有一堵总长为24 m的“L”形墙ECF，其中EC⊥CF，且EC=CF，利用这堵墙和长为am的篱笆围成一个矩形养鸡场，怎样围面积最大？最大面积是多少？

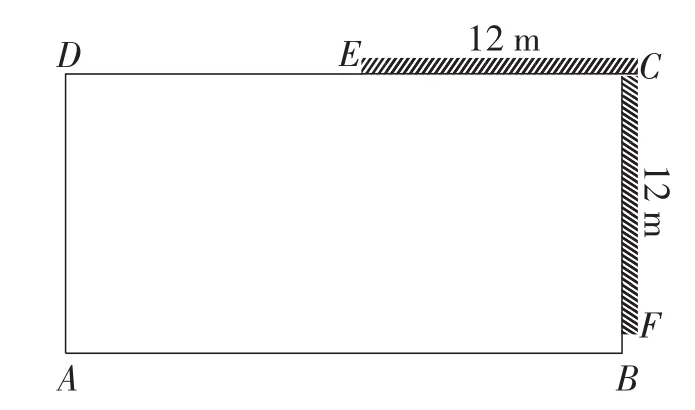
图3

解析：类似于上面的分析，先把这堵墙看成一段特殊的篱笆，则共有篱笆()a+24 m.

同上面的研究得到当这些篱笆围成边长为的正方形时，其面积最大.

再分类讨论如下.

（1）若即a≥24时，同上，以这堵“L”形墙为基础，围建成边长为的正方形，便得到了符合题意的面积最大的养鸡场，此时养鸡场最大面积为

（2）若即当a＜24时，同上，矩形与“L”墙的位置关系归纳为两种：矩形“仅有一边靠墙”或矩形“相邻两边都靠墙”.

由于CE=CF，不失一般性，不妨假设CD边总是靠墙CE，如图4和图5所示.

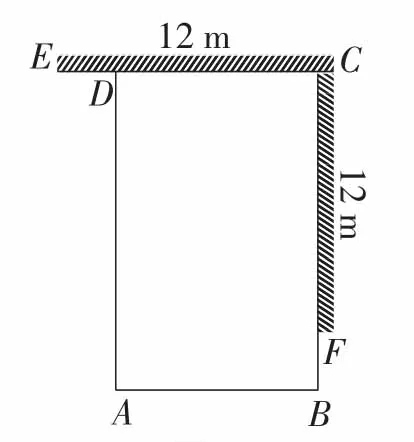
图4

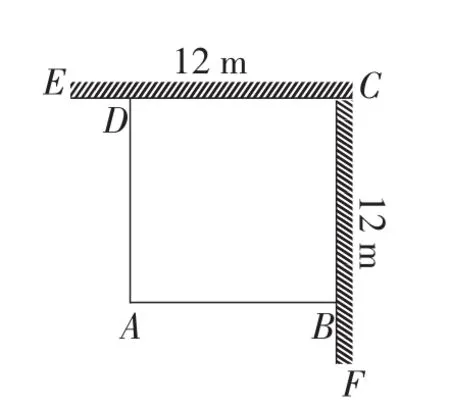
图5

注意上面第（1）种情况中的一个特例：当a=24时，取得最大面积的养鸡场恰好是以“L”形墙为相邻边的正方形（此时矩形相邻两边都靠墙）.

因此，我们可以肯定，当a＜24时，矩形若要取得最大面积，其相邻两边都要靠墙，如图5所示.

设AB=x，

则AD=a-x.

所以

显然当时，S矩形ABCD有最大值此时矩形的长和宽都为最大面积是

篱笆围成矩形面积最大值问题，确实是一个易被学生操作理解，易于形成数学模型的综合性载体.实际上，我们还可以寻找新的观察点再深入研究，这里不再赘述.

［1］祝立新.篱笆怎么围面积最大［J］.中国数学教育（初中版），2017（3）：9-11.