研读中考试题·培养数学素养·提升解题能力——2017年天津市中考第24题的解题研究与反思

（天津市滨海新区塘沽第六中学；天津市教育教学研究室；天津市滨海新区塘沽教育中心）

让学生在实践中反思，在反思中体验，在体验中感悟，在感悟中提升，这是数学教学的本真，也是笔者研读2017年天津市中考试卷第24题的切身感受.

一、试题呈现

题目将一个直角三角形纸片ABO放置在平面直角坐标系中，点点B(0，1)，点O(0，0).P是边AB上的一点（点P不与点A，B重合），沿着OP折叠该纸片，得点A的对应点A′.

（1）如图1（1），当点A′在第一象限，且满足A′B⊥OB时，求点A′的坐标.

（2）如图1（2），当P为AB中点时，求A′B的长.

（3）当∠BPA′=30°时，求点P的坐标（直接写出结果即可）.

图1

二、试题特色

此题是坐标系下的图形翻折变换，运用图形与坐标、图形与函数、图形与变换等知识，体现知识与能力并用、思想与方法交融的命题特点，也符合“起点低，坡度缓，尾巴翘，宽进严出”的命题要求.此题重点考查了学生的几何推理能力，思维层次逐步提升，“几何味”逐步显现，梯度合理，区分度较高.逻辑推理是学生发展所需要的重要核心素养之一，本着“核心内容重点考查”的命题指导思想，命题者在这方面有所侧重，突出对学生的数学思想方法、画图能力、计算能力、知识应用能力等数学素养的考查.

三、解法探究

解析：（1）由翻折的性质，得△OPA′≌△OPA.从而得

又由A′B⊥OB，根据勾股定理，可以求出BA′的长，从而得到点A′的坐标.

（2）（方法1）由已知，可得∠BAO=30°，∠OBA=60°，AB=2.

因为P为AB中点，∠AOB=90°，

所以OP=PB=AP=1.

所以△BOP为等边三角形.

所以∠BOP=60°，且∠POA=∠PAO=30°.

由翻折的性质，得△OPA′≌△OPA.

得∠OPA′=∠OPA=120°，且AP=A′P.

从而得∠BOP+∠OPA′=180°.

因此OB∥A′P.

因为OB=A′P=1.

所以四边形OPA′B是平行四边形，此时A′B=1.

或者由OB=OP，得四边形OPA′B是菱形，从而得A′B=1.

阅卷中发现问题：在证明四边形OPA′B是菱形时，学生误认为对角线互相垂直的四边形就是菱形，或者多次证明三角形全等.证明时的逻辑关系不清楚，说明学生对几何定理掌握不准，导致逻辑推理存在问题.

（方法2）由方法1可知 ∠OPA′=∠OPA=120°，且△BOP为等边三角形，即∠OPB=60°.得 ∠BPA′=60°.又由PB=AP′=1，得到△A′PB为等边三角形，此时A′B=1.

阅卷中发现问题：有些学生不会用，或者不知道直角三角形斜边上的中线这一性质；有些学生对∠BPA′=60°的证明说不清楚，误认为是由翻折得到的.

（方法3）由方法1可知△BOP为等边三角形，即∠OPB=60°.得 ∠POA=∠PAO=30°.由翻折的性质，可以得到∠POA′=∠POA=∠BOA′=30°.因为OB=OP，所以OA′是线段PB的垂直平分线.从而得AB′=A′P=1.

或者如图2，连接A′A.由方法3可知∠POA′=∠POA=30°.得∠A′OA=60°.从而得△A′OA为等边三角形.由OP=A′P，得PA是线段A′O的垂直平分线，直接得到BA′=OB=1.

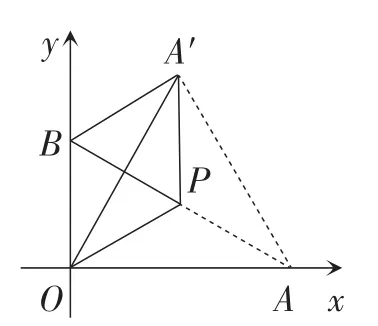
图2

这就是对基础知识、基本技能的升华，抛开现象，还原问题本真，也是教师追求的最高目标，即教会学生学会求知.

阅卷中发现问题：部分学生不敢在图中标字母，导致对很简单的问题表述不清楚.若设BP与A′O的交点坐标为点E，再证垂直平分线就方便了.另外，有些学生不会运用等腰三角形三线合一的性质，导致证明受阻.

（方法4）如图3，过点A′作A′H⊥Oy于点H.

由方法3可知 ∠AOA′=60°.又由 ∠BOA=90°，得∠HOA′=30°.由已知可证△A′BP为等边三角形.得∠HBA′=60°.

根据翻折的性质，得

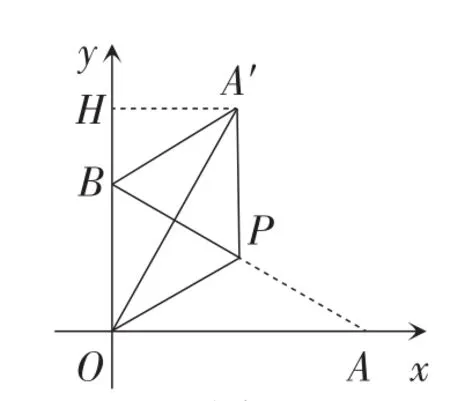
图3

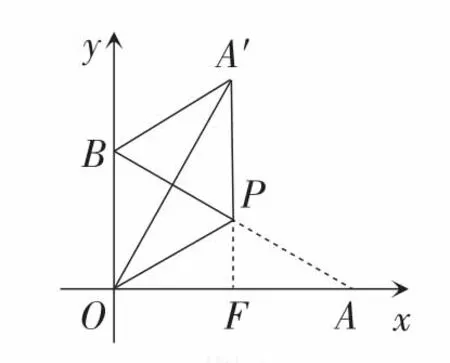
图4

（方法5）如图4，延长A′P交OA于点F，可证得A′P⊥OA.从而求出得到点A′的坐标为代入两点间距离公式，从而可求出A′B的长.

阅卷中发现问题：部分学生过点P作PF⊥OA于点F，就认为A′，P，F三点共线，直接得到点A′的坐标.这里实际上需要先证明三点共线，这一细节失分严重.

第（2）小题思考路径：研究基本图形，一种是面对“有形”的状态，即图形是真实存在的，需要在确定的图形中讨论各基本要素的关系.例如，方法1、方法2、方法3中要求A′B的长，需要找到与A′B相等的线段.由已知条件可知OB=OP=BP=PA=PA′=1.再联想基本图形（平行四边形、菱形、等边三角形、等腰三角形）解决问题.此小题命题指向明确，思路顺畅，使解法自然生成.另一种则是面对“无形”的状态，即图形的呈现不完整，需要通过适当添加辅助线构造基本图形；或者，将已有的知识经验，迁移至新的情境中，使问题得解.例如，方法4、方法5添加辅助线后，用两点间距离公式求解.

（3）情况1：如图5，裁一块与△BOA全等的三角形，滑动折痕OP，使得∠BPA′=30°，找到点A′的位置，可以发现∠BPA′=∠BA′P=30°.

图5

因为∠OBA=60°，

所以点A′在y轴上，且OP平分∠AOA′.

（方法1）如图6，作PH⊥OA于点H，

设OH=PH=x，则

利用

求得点P的坐标为

图6

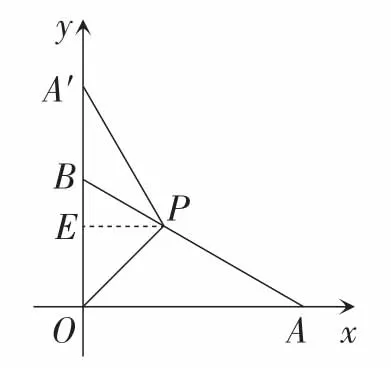
图7

（方法2）如图7，作PE⊥Oy于点E.

由翻折的性质，得从而得再用cos∠BPE=30°可以求出从而求得点P的坐标为

（方法3）如图7，作PE⊥Oy于点E，得BP=A′B=利用△BPE∽△BAO，求出即点P的坐标为

（方法4）由已知可得直线OP的解析式为y=x，直线AB的解析式为联立方程组可求得点P的坐标.

情况2：（方法1）如图8，将点P继续向AB方向滑动，得∠BPA′=∠BAO=30°.可知A′P∥Ox.

由∠A=∠A′=30°，∠OBA=60°，得A′P⊥OB.

过点P作PH⊥OA，与OA交于点H.设OB与A′P的交点为点D，则

在Rt△PHA中，由∠OAB=30°，可得

从而得

因此点P的坐标为

图8

（方法2）由方法1，得在Rt△BDP中，∠BPD=30°，从而可求出点P的坐标.

（方法3）可先由已知求出直线BA的解析式y=再带入点P的纵坐标求出点P的横坐标即可.

（方法4）利用△BPD∽△BAO，可求出点P的坐标.

第（3）小题思考路径：此问中，动点P由AB中点滑动到一般位置，又增加了∠BPA′=30°的条件.通过折纸确定点P的位置，生成新的条件，构成新的要素之间的关系，再作辅助线，得到特殊三角形，还原到解直角三角形，从而求出点P的坐标.此问主旨是在图形运动变化（改变位置关系）的过程中，研究图形中的要素之间发生了怎样的变化（位置关系和数量关系）.

四、反思与提升

第（2）小题的解题方法多，综合性强，渗透了数学基本思想方法和基本技能，值得思考研究.此道小题挖掘题目内在的内容，合理运用基本图形，做到了数形结合，转化明确，使解法自然生成.在变化过程中，找不变的关系，并且合理地运用函数思想、数形结合思想、转化思想、分类讨论思想.此题目的3道小题间层层递进，到第（3）小题达到升华.

第（3）小题需要提升学生的动手能力，这种方法可以运用到课堂教学之中.特别在九年级综合复习阶段，教师要把手放开，大胆让学生去尝试，让学生在做中学习，感悟学习过程，这也是让学生学会学习、学会求知、学会建模的理念.提高学生的画图能力也是教师需要提升的理念.理念新了，方法自然就活了.

“真正的数学题”应该满足一些基本条件：与重要的数学概念和性质相关，体现基础知识的联系性，解题方法自然、多样，具有自我生长的能力等.2017年天津市中考试卷第24题的3道小题形成一个逻辑联系紧密的整体，渗透从特殊到一般的研究方法，关注核心内容，关注知识联系，关注过程考查，关注思维层次，关注试题的思想性，是一道值得师生品味的好题.它可以作为课堂教学的资源，为教师的“教”和学生的“学”服务，也可提升教师的教学能力.

“图形的性质”部分的综合题，出现的图形比较多，几何关系复杂，突出考查学生应用基本思想方法、基本活动经验去分析和解决问题的能力.在日常教学中，教师要教会学生运用已有的数学活动经验，在复杂的几何图形中，分解出简单的、基本的图形，或是通过添加辅助线构造基本图形，合理运用图形基本性质描述、分析和解决问题.

在解决坐标系下翻折、旋转、平移变换的问题中，教师可以指导学生动手折一折、做一做，在做中感悟学习过程，还原数学本真，感受数学学习的真谛，激发学生学习数学的兴趣，提升学生解决数学问题的能力.

［1］刘家良.由形到质 异中求同 积淀思想：2014年天津市中考第25题评析及教学导向［J］.中国数学教育（初中版），2015（4）：58-60.

［2］章建跃.发挥数学的内在力量 为学生谋取长期利益［J］.数学通报，2013（2）：1-6，10.

［3］姜晓翔.孕育“思维过程” 反思“解题方法”：由一次教师说题比赛刍议“解题教学”［J］.中国数学教育（初中版），2014（7/8）：74-78.

［4］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［5］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.