超声探头发射声场模拟及其缺陷响应研究*

李雪梅，汤长波，谢勇君，唐文斌，陈综艺

(1. 桂林电子科技大学 机电工程学院, 广西 桂林 541000；2. 暨南大学 电气信息学院, 广东 珠海 519070)

0 引言

近年来，超声检测技术因其具有检测范围广，检测灵敏度高，成本低，速度快，操作方便等优点在工业实际当中得到了广泛的应用[1-2]。在对被检工件进行超声检测之前，一般需要通过实验验证的方法来确定合适的检测参数和检测方案，会耗费大量的时间和成本，降低检测的效率。当检测到缺陷之后，还需要使用大量的对比试块对缺陷进行定量分析，这大大增加了实验成本[3]。针对以上问题，超声探头发射声场模拟和缺陷响应研究就具有十分重要的意义。

超声探头声场模拟常用的理论方法有瑞利积分法和多元高斯声束叠加法[4]。其中，瑞利积分法计算精度很高，但是很难获得解析解，计算量大。多元高斯声束叠加法计算速度快，更加容易获得声场解析表达式。陈友兴等采用多元高斯声束叠加法对圆柱体进行了声场仿真，但是只研究了曲界面对超声声场的影响，没有涉及其他的检测参数[5]。张书增等基于基尔霍夫近似建立了横通孔缺陷散射声场模型，但是并没有对小尺寸夹杂类缺陷进行研究[6]。

本文基于多元高斯声束叠加理论，进行了超声探头发射声场建模，并且研究了各检测参数对探头发射声场的影响。同时将多元高斯叠加方法与波恩近似方法相结合，建立了夹杂类缺陷回波模型，模拟了夹杂类缺陷回波信号，并通过实验验证了该模型的有效性。

1 基于多元高斯声束发射声场建模

1.1 发射声场的理论方法

多元高斯声束叠加法是通过多个单高斯声束叠加得到多元高斯声束。J J Wen和M A Breazeale从亥姆霍兹波动方程开始推导，得出高斯声束的基函数，然后根据边界条件进行基函数的叠加，并且计算得出相对应的叠加系数[7]。L W Schmerr对多元高斯声束叠加理论进行了进一步的概述，并将其用于圆形活塞探头的发射声场模拟[8]。根据多元高斯声束叠加法，超声探头表面的声场公式为：

(1)

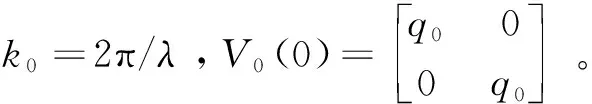
q0为与声束腰w0和探头半径R相关的参数。

式(1)可以简化表示为：

p(x,y,0)=P(0)exp(ik0φ(0))

(2)

当声束传播到液固界面的时候，声场的表达式为:

p(x,y,D)=P(D)exp(ik0φ(D))

(3)

高斯声束在液体中传播的时候，声压振幅会不断的衰减。当高斯声束传播到液固界面的时候，振幅可以表示为：

(4)

式中,V0(D)=V0(0)+DI,I为二维单元矩阵。

高斯声束在液体中传播的时候，发生的相位变化可以表示为：

(5)

当高斯声束通过液固界面的时候，振幅变化可以表示为：

(6)

式中，ρ0表示液体介质的密度；c0表示液体介质中的声速；T表示液固界面的穿透系数。超声垂直入射时穿透系数表达式为：

(7)

式中，Z1、Z2为介质的声阻抗。

界面固体一侧高斯声束的相位表达式为：

(8)

式中，V1(0)的表达式为：

(9)

(10)

[V1(0)12]=[V1(0)21]=0

(11)

高斯声束通过液固界面进入到固体介质之后，振幅变化可表示为：

(12)

(13)

固体介质中的相位表达式为：

(14)

将各项表达式进行组合并且引入探头表面质点振动速度v0，可以得到单高斯声束的表达式：

(15)

使用高斯叠加系数An、Bn将15个高斯声束进行叠加可以得到圆形活塞探头在液体中的声场表达式为：

(16)

圆形活塞探头在固体中声场表达式为：

(17)

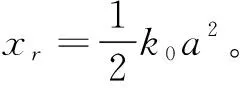
1.2 发射声场的仿真与分析

根据超声在液体中的声场表达式(16)，使用Matlab仿真工具对圆形探头在液体中的声场进行仿真。选取水作为液体传播介质，水的纵波传播速度和密度分别取1000kg/m3、1500m/s。图1为探头发射频率3MHz，探头尺寸分别为8mm、10mm、12mm时，各圆形探头在水中的二维发射声场。图2为探头尺寸6mm，探头发射频率分别为3MHz、4MHz、5MHz时，各圆形探头在水中的二维发射声场。从图1中可以得出，随着探头尺寸的不断增大，声束宽度不断扩大，同时声束主瓣的辐射长度随之增大，副瓣数量增多。从图2中可以得出，随着探头发射频率的增大，声束主瓣的辐射长度越来越大，副瓣数量增多，声束能量越来越向中部集中，同时在远场区声束逐渐变窄，覆盖范围降低。

图1 探头尺寸分别为8mm、10mm、12mm的圆形探头二维声场

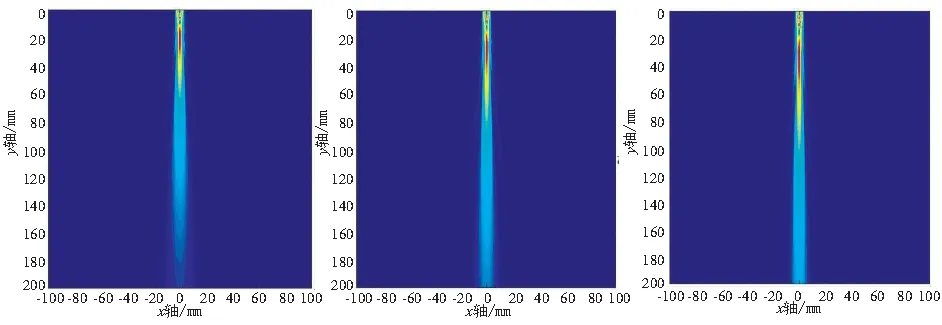
图2 探头频率分别为3MHz、4MHz、5MHz圆形探头二维声场

式(17)表示的是圆形探头的发射声场，对于矩形探头发射声场可以使用两个圆形探头的乘积来表示[9]，矩形探头的发射声场表示为:

(18)

对于聚焦探头，需要将式(17)中的高斯叠加系数Bn改为Bn+ik0a2/(2F)[10]，其中a为探头尺寸，F为几何焦距。图3为圆形普通、矩形、圆形聚焦三种探头在水中二维声场对比示意图。从图3中可以得出，在探头发射频率和探头尺寸相同的前提下，三种类型的探头发射声场的能量都是集中在主瓣中部，其中圆形普通探头副瓣数量最多，能量发散最为厉害，但是声束宽度也是最大的，声束辐射距离最远。圆形聚焦探头发射声场刚开始时能量最为集中，声束最窄，随着传播距离的增加，声束开始不断发散，副瓣数量增加，声束辐射距离是最近的。矩形探头发射声场刚开始时，声束宽度介于圆形普通探头和圆形聚焦探头之间，随着传播距离的增加，声束发散程度最小，副瓣数量最少，声束辐射距离介于圆形普通探头和圆形聚焦探头之间。

当超声在不同的介质中传播时，不同的界面会产生不同的探头发射声场。当超声垂直入射到平界面时，式(9)、式(10)中的k0、k1为0；界面为凸界面时，k0×k1>0；界面为凹界面时，k0×k1<0[11]。采用水浸法探伤，固体介质为钢，水程60mm，探头频率为6MHz，探头尺寸为8mm，分别在平界面、凸界面、凹界面三种条件下，对探头发射声场进行仿真，如图4a～4c所示。从图4a中可以看出超声在通过水钢平界面进入固体中的时候，声压值迅速增大，然后随着传播距离的增加声束不断发散。这是由于水的声阻抗要比钢的声阻抗小的多，根据式(7)可知超声垂直入射水钢界面时穿透系数为1.935，即穿透声压可以表示为入射声压的1.935倍，所以钢中的声压值较大。从图4b、图4c中可以看出当超声通过水钢凸界面时发生了一定程度的聚集变化，声束能量比通过平界面时更加集中，声束主瓣辐射距离加长；当超声通过水钢凹界面时发生了一定程度的发散变化，声束能量分散严重，声束主瓣辐射长度缩短。

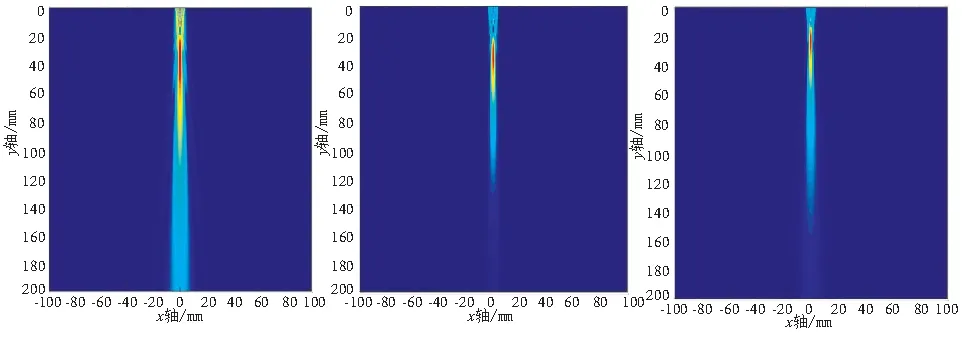
图3 圆形普通探头、矩形探头、聚集探头二维声场对比示意图

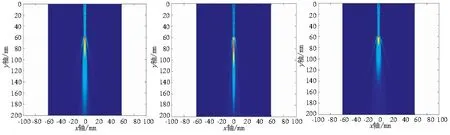
(a)平界面 (b)凹界面 (c)凸界面

2 基于波恩近似的夹杂类缺陷回波模型

在超声检测中，夹杂类缺陷很难通过当量法进行定量分析。波恩近似基于低频近似，使用量子力学中的积分方程代替了传统的偏微分方程来描述超声场散射问题[12]。对于小尺寸的夹杂类缺陷散射声场问题，采用波恩近似来处理精度更高。基于波恩近似建立夹杂类缺陷回波模型。根据奥尔特互易原则，超声探头接收到的缺陷回波信号可以表示为:

(19)

式中,a2代表探头的面积，a2ρ0c0=Z，Z代表探头的阻抗。ρ0c0和ρ1c1分别代表探头和传播介质中的密度和声速。s(w)为系统函数，在探头特性参数和系统函数幅值已知的情况下可直接建立系统函数模型。v(m,w)代表缺陷上m点的质点振动速度，该值可以通过基于多元高斯声束的发射声场公式(20)获得。

(20)

式(19)中A(m,w)表示缺陷散射声场振幅，采用波恩近似对夹杂类缺陷散射声场进行表示。

(21)

式中，A(m,w)、B(m,w)分别表示散射后的纵波振幅和横波振幅，α、β分别表示纵波和横波的波矢。对于纵波入射的散射声场的振幅可以表示为:

(22)

式中，S(α,α′)为描述缺陷的形状因子。λ,μ,ρ分别为传播介质的弹性常数和密度。

3 夹杂类缺陷回波模型的实验验证与分析

夹杂类缺陷回波模型的实验采用水浸式探伤。实验系统主要包括PCI超声探伤卡、工控机、超声探头和试块。实验系统中的PCI超声探伤卡选用汕头超声电子公司生产的CTS-04PC超声探伤卡，超声探头尺寸为4×4mm，发射频率为2MHz。水程为70mm，密度选取1000kg/m3，声速选取1500m/s。试块主介质为钢，密度选取7800kg/m3，纵波声速选取5900m/s，夹杂缺陷介质为钛，形状为球形，半径尺寸为1mm，密度选取4500kg/m3，深度为30mm。实验过程中，不断调整探头的位置，使探头中心与缺陷中轴线相对应，探头接收到缺陷的发射回波，通过超声探伤卡转化为电压信号，然后在工控机显示屏上进行显示。实验所获取的波形图如图5所示。根据式(19)，确定各项参数之后，使用Matlab仿真软件对夹杂类缺陷回波模型进行仿真，获取夹杂类缺陷相应的频率特性之后，通过反傅里叶变换转化为缺陷相应的时域信号，并且以缺陷回波的形式进行显示。夹杂类缺陷回波仿真效果图如图6所示。图7为夹杂类缺陷回波仿真效果和实验效果对比示意图。

通过仿真效果和实验效果对比可以得出，两信号的主体部分的形状特征比较吻合，各峰值相对误差可以保证在10%以内。由此可以证明该夹杂类缺陷回波模型的正确性。分析两信号幅值产生差异的原因，由于仿真模型是在理想状态下进行的，所以仿真信号较为平滑，而实际检测过程中，受到探伤水平和实验条件的影响，会出现一些杂波，对实验效果造成一定的影响。

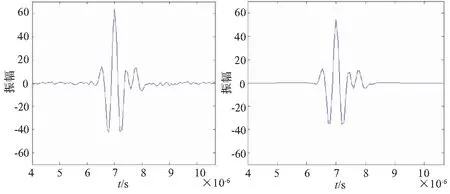
图5 实验效果图 图6 仿真效果图

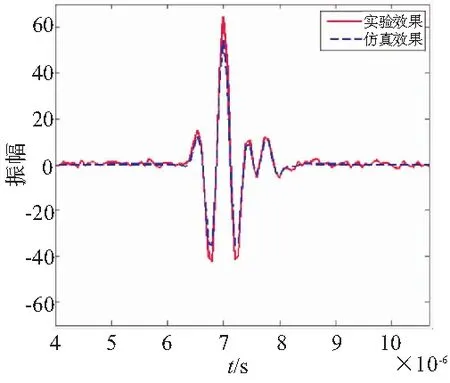
图7 实验效果和仿真效果对比示意图

4 结论

本文建立了基于多元高斯声束的发射声场模型，研究了探头发射频率、探头尺寸、探头类型和入射界面对探头发射声场的影响，为实际超声检测中确定合适的检测方案提供了一定的理论指导；在前期建立的多元高斯声束探头发射声场模型的基础上，结合波恩近似理论，建立了夹杂类缺陷回波模型，并通过实验验证了该模型的有效性，为夹杂类缺陷的定量分析提供了一定的理论指导，有利于降低实验成本，提高超声检测的效率。

[参考文献]

[1] 钟柳春, 毕庆贞, 张凯, 等. 一种基于超声波测厚的薄壁件自动补偿加工方法[J]. 组合机床与自动化加工技术, 2016(10): 148-150.

[2] 鲁帅帅，昃向博，付秀丽. 超声波光整强化40Cr表层显微硬度研究[J]. 组合机床与自动化加工技术, 2014(12): 27-29.

[3] 丁辉. 计算超声学[M]. 北京: 科学出版社, 2010.

[4] 沙正骁, 刚铁, 赵新玉. 超声换能器声场的模拟和可视化研究[J]. 无损检测, 2011, 33(5): 2-6.

[5] 陈友兴, 席海军, 郭文静, 等. 基于多元高斯声束模型的圆柱体三维声场仿真[J]. 火力与指挥控制, 2015, 40(6): 139-144.

[6] 张书增, 李雄兵, 杨岳, 等. 钢轨轨头多元高斯声场模拟及其缺陷响应[J]. 铁道学报, 2014, 36(1): 76-80.

[7] J J Wen, M A Breazeale. A diffraction beam field expressed as the superposition of Gaussian beams[J]. Journal of the Acoustical Society of America,1988, 83: 1752-1756.

[8] Huang R, Schmerr L W, Sedov A. Multi-Gaussian ultrasonic beam modeling for multiple curved interfaces—an ABCD matrix approach[J]. Research in Nondestructive Evaluation, 2005,16(4): 143-174.

[9] 段晓敏, 赵新玉, 孙华飞. 矩形表面波探头声场的高斯声束叠加法[J]. 物理学报, 2014, 63(1): 1-6.

[10] 李力, 姜恺, 曾德学. 基于多元高斯模型的超声声场仿真系统设计[J]. 三峡大学学报(自然科学版), 2014, 36(2): 77-80.

[11] Best S R, Croxford A J, Neild S. Modeling harmonic generation measurements in solids[J]. Ultrasonics, 2014,54: 442-450.

[12] 李太宝. 计算声学[M]. 南京: 南京大学出版社, 2003.