基于粒子群算法的机器人关节空间最优运动轨迹规划*

冯 斌，刘 峰，郑飂默，3

(1.中国科学院大学， 北京 100049；2.中国科学院沈阳计算技术研究所，沈阳 110168；3.沈阳高精数控智能技术股份有限公司 高档数控国家工程研究中心，沈阳 110168)

0 引言

随着工业自动化程度的提高，对机器人的要求越来越高。轨迹规划是机器人控制的关键[1]。也是近几年研究的热点。目前轨迹规划优化分为两种：一种是对时间进行优化，另一种是对系统能量进行优化。为了提高机器人的工作效率，对机器人关节空间运动轨迹进行优化。选择运动时间作为优化对象可以提高机器人工作效率，改善机器人的性能。论文中将采用粒子群算法完成对机器人关节空间运动轨迹的时间优化。

对轨迹规划进行时间优化有多种方法，如采用遗传算法[2-5]，粒子群算法[6-9]等。当前国内外多数机器人关节空间轨迹研究都是采用遗传算法展开，如文献[2-5]。采用粒子群算法还需要进一步探讨研究，但也有一定的研究基础，如文献[6-9]都是采用粒子群算法在轨迹规划方面展开研究。将作为论文研究的基础。

论文选用PUMA560机器人为例，研究机器人点到点之间的轨迹规划时间。采用高次多项式插值和粒子群算法，完成对轨迹规划运动时间的优化。通过实际测试和仿真实验相结合验证研究结果的实用性和预期结果。实验表明，该方法不仅可以完成对轨迹规划时间的优化，缩短了机器人关节空间运动的时间，缩短40%左右，而且可以在实际中应用。这对于改善机器人的性能，提高工作效率有很大的帮助。

1 PUMA560机器人运动学分析

PUMA560是一款6自由度的机器人，它的D-H参数如表1所示。根据D-H参数表可以构造机器人模型。表中的为变量θ，a和d为常量。其中a1=0.4318,a2=0.0203,d3=0.1501,d4=0.4318。本文中将使用Robotics Tools 9.0中的PUMA560机器人模型及相应的函数。

表1 PUMA560机器人的D-H参数

对PUMA560关节机器人运动学原理及仿真进行详细分析[10-11]，结合MATLAB机器人仿真库，可以求得机器人运动的正解和逆解。为了对机器人的关节空间运动进行规划，需要求得关节运动的位置点。根据机器人逆运动学特征可以求出关节的运动位置点。

为了确保机器人末端爪手的笛卡尔空间坐标是可达的，选择使用机器人的正向运动求解起点和终点。起点位置用js=[0 0 0 0 0 0]求得，终点用je=[pi/2 0 pi/2 0 0 pi/2]求得。根据MATLAB机器人仿真函数库Robotics Tools 9.0对其进行正向求解。式(1)求得末端爪手的起点位置，式(2)求得末端爪手的终点位置。式子中的fkine()为求正解函数，p560为PUMA560机器人模型，js和je为各关节起止位置的角度关节起止位置的角度，Hs和He为末端的齐次变化坐标矩阵。

Hs=fkine(p560,js)

(1)

He=fkine(p560,je)

(2)

为了将路径分为多个区间，使用函数ctraj()将路径分为多个区间，如式(3)所示：

Hc=ctraj(Hs,He,4)

(3)

Hc中包含4个齐次变换坐标矩阵，将路径分为3个区间。由Hc可以获得4个路径点的笛卡尔空间坐标点，如表2所示。

表2 机器人末端运动轨迹路径点

根据齐次坐标变换矩阵可以求得机器人的运动学逆解，即求得关节运动轨迹区间路径点。求逆解如式(4)所示：

Q=ikine6s(p560,Hc)

(4)

式(4)求得关节的路径点解，前3个关节的路径点的解如表3所示。

表3 路径点各关节的解

2 基于粒子群算法[12]的实验设计

(1)采用高次多项式插值的方法对机器人关节空间运动进行插值，实验中将关节空间运动路径分为3个区间。设关节运动的位置为q1～q3，不同区间的时间为t1～t3。关节空间运动位置与时间的关系如式(5)～式(7)所示：

(5)

(6)

(7)

根据式(5)～式(7)可以求出机器人关节运动各点的速度和加速度计算公式。速度计算如式(8)～式(10)所示，加速度如式(11)～式(13)所示。

(8)

(9)

(10)

(11)

(12)

(13)

根据已知条件，不同时刻所经过的路径点和不同时刻机器人的运动状态，可以得出以下3组式子。设4个路径点的值为Q(1)～Q(4)，3个区间的运动时间为t(1)～t(3)。

第一区间求解参数公式如式(14)所示：

(14)

第二区间求参数公式如式(15)所示：

(15)

第三区间求参数公式如式(16)所示：

(16)

根据式(14)～式(16)可以求出高次多项式的参数。从而可以求出关节空间运动的轨迹公式、速度公式和加速度公式，可以根据公式求出任意时刻的位置、速度和加速度。

(2)基于粒子群算法的关节空间轨迹规划优化需要选取若干粒子作为优化对象。实验中以完成三个区间的运动所用时间(t1,t2,t3)组成一个三维粒子，随机生成20组粒子。粒子的值均在[4,5]之间。粒子的适应函数如式(17)所示：

fitness=t1+t2+t3

(17)

根据适应度函数计算粒子的适应度值。选取单个粒子中适应度值最小的作为局部最优粒子pBest和所有粒子中适应度值最小的作为全局最优粒子gBest。

除适应度函数外还需要确定更新粒子速度公式(18)中的各个参数。惯性权重W，W最大为Wmax=0.9，最小为Wmin=0.5，W随着迭代次数n的增加不断减小，变化如公式(20)所示。学习因子C1和C2均为1.5。随机因子r1和r2为[0,1]之间的随机数，通过MATLAB函数rand()生成。

v[m]=w·v[m]+c1·r1·(pBest[m]-
present[m])+c2·r2·
(pBest[m]-present[m])

(18)

present[m]=present[m]+v[m]

(19)

W=Wmax-(Wmax-Wmin)·(n/N)

(20)

在本次实验过程中除了满足普通约束条件外还需要满足机器人关节空间运动的 约束条件，即关节运动的速度和加速度不能超过规定的最大速度Vmax和最大加速度amax。由公式(8)～公式(13)可以求出不同粒子下的最大速度V和最大加速度a。所以约束条件如式(21)所示：

(21)

通过带约束条件的粒子群优化算法完成对关节空间运动轨迹规划的时间优化，获得关节运动的最短运动时间。

实现优化过程，首先验证粒子是否符合式(21)中的约束条件。满足则使用式(17)将适应度值计算出来，否则置为无穷大。将各个粒子的适应度值保存起来。从20个粒子中通过比较适应度值，选取适应度值最小，即完成规划运动所用时间最少，作为全局最优粒子。通过N次迭代不断更新粒子，计算适应度值，选出最优粒子，从而得到约束条件下的最优解，即关节空间轨迹规划最短时间。

3 实验验证及结果分析

本文中采用基于粒子群优化算法的高次多项式插值方法对机器人关节空间运动进行轨迹优化。保证了关节运动轨迹的平滑稳定。

对于关节机器人如图1a所示，是一款自主研发的关节型通用机器人，运动精度高，灵活性好，结构紧凑，占地面积小，可连续作业，提高设备的利用率，保障生产效率，可运用于机床上下料等多个领域。

为了最大限度的发挥该款机器人的优势，自主研发了与该款机器人配套的专用控制器，如图1b所示。图1b中的控制器具有简单易用的操作界面和国际领先的总线数据传输形式，非PLC控制，降低干扰，定位更精确，响应速度快，可存储多种程序，换产更便捷。

(a)关节型通用机器人 (b)关节型通用机器人控制器图1 关节型通用机器人

将优化程序加入控制终端，通过控制器操作可以完成预期的轨迹运动。说明该轨迹优化算法可以运用于实际机器人控制中。

按照图1a、图1b所示的机器人与控制器之间的工作原理在表4中的约束条件下进行仿真验证，各个关节的速度和加速度约束条件如表4所示。

表4 速度和加速度约束条件

得到以下结果。关节运动的位置和时间关系如图2所示。

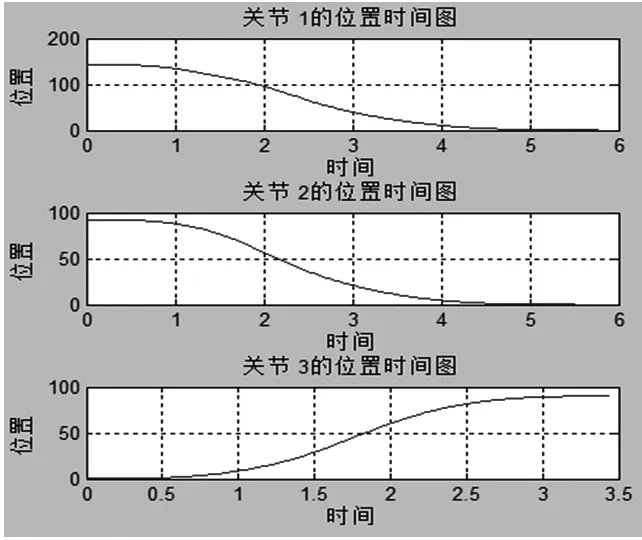
图2 位置-时间关系图

关节运动的速度和时间关系如图3所示，从图中可以看出速度在整个运动过程中都是连续的。

图3 速度-时间关系图

关节运动的加速度和时间关系如图4所示，从图中可以看出整个过程中加速度是连续的，并且在开始和终止时都为零，使关节能够平稳的停下来。

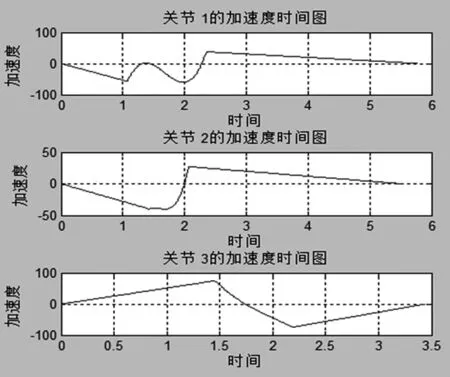
图4 加速度-时间关系图

关节空间轨迹运动时间与迭代次数的收敛关系如图5所示，从图中可以看出迭代若干次之后，时间快速收敛到最优时间。

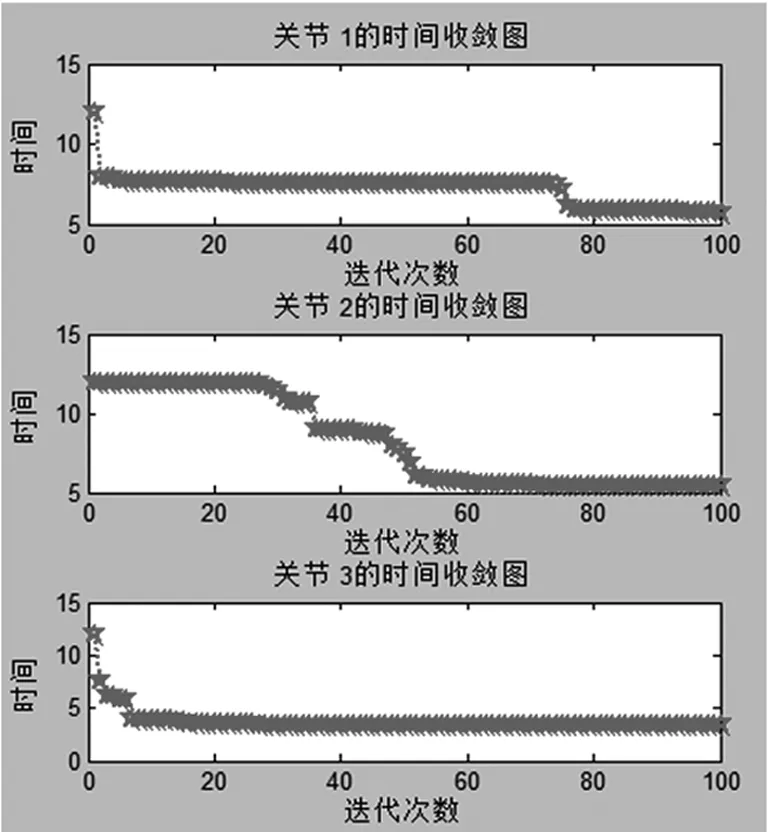
图5 时间收敛图

从图2中可以看出关节在相应的时刻到达预期的位置。从图3中可以看出，关节的起始速度和结束速度均为0，并且运动过程速度连续，保证了机器人关节运动的稳定。从图4中可以看出关节运动的加速度连续，并且始末加速度均为0，既保证了机器人关节运动的稳定性，减少了关节运动过程中的震荡。

在图2～图4的前提下，以关节1的优化结果为例得出如表5所示的优化结果。

表5 关节优化结果

从表5中可以看出，完成规定的运动初始时间是12s。经过优化后有了明显的改善，由原来的12s降到了现在的7.4s甚至5s就可以完成，说明该方法真实可行。在保证运动轨迹平滑稳定的前提下，提高了机器人的工作效率。

4 小结

通过论文中的设计实验使机器人关节空间轨迹运动时间缩短超过40%，由原来的12s缩短到优化后的7.4s。与使用遗传算法等优化算法比较，用粒子群算法对机器人空间轨迹进行优化，不仅优化结果明显，而且粒子群算法结构简单，易于实现。结果表明按照论文中的方法对机器人的关节空间轨迹运动时间进行优化，对改善机器人的性能有很大帮助。

论文中的实验是使用基于约束条件下的粒子群算法进行优化。通过改进粒子群算法也能完成对机器人关节空间运动轨迹时间优化，优化的关键点在于选取优化对象，如可以选取路径点作为优化目标等。后续将在这些方面展开进一步研究。

[参考文献]

[1] 马睿,胡晓兵,殷国富,等.六关节工业机器人最短时间轨迹优化[J].机械设计与制造,2014(4):30-32,35.

[2] 马丹妮,李传江,张自强.基于遗传算法的七自由度机器人轨迹规划[J].实验室研究与探索,2016(9):33-37.

[3] 赫建立,朱龙英,成磊,等.基于遗传算法的6-DOF机器人最优时间轨迹规划[J].机械传动,2015(9):41-45.

[4] 郭清达,万传恒,史步海.基于遗传算法的工业机器人时间最优轨迹规划及仿真研究[J].计算机测量与控制,2014,22(4):1240-1242.

[5] 恽为民,席裕庚.基于遗传算法的机器人关节空间最优运动规划[J].机器人, 1995(4): 206-217.

[6] 勾月凯,葛为民,王肖锋,等.基于粒子群算法的可重构模块化机器人速度约束下轨迹规划[J].天津理工大学学报,2016,32(5):6-11,47.

[7] 李小为,胡立坤,王琥.速度约束下PSO的六自由度机械臂时间最优轨迹规划[J].智能系统学报,2015,10(3):393-398.

[8] Fang Gao,Qiang Zhao,Gui-Xian Li. Path Planning of Continuum Robot Base donaNew Improved Particle Swarm Optimization Algorithm [J].Journal of Harbin Institute of Technology,2013(4):78-84.

[9] Ellips MASEHIAN, Davoud SEDIGHIZADEH. Multi-objective robot motion planning using aparticle swarm optimization model [J].Journal of Zhejiang University- Science C(Computers & Electronics),2010 (8):607-619.

[10] 于楚泓.基于MATLAB的机器人运动学建模及仿真分析[J].机电信息,2017(9):78-79.

[11] 董慧颖,梁爽.基于MATLAB的PUMA560机器人运动学仿真[J].无线互联科技,2014(5):179-180.

[12] 姚禹.粒子群优化算法的发展及应用[J]. 信息记录材料,2009(4):50-54.