基于改进支持向量机的产品服务系统客户流失预测模型*

王 涛，丛 茜，尚钰量，程 辉，张在房，樊蓓蓓

(1.上海航天设备制造总厂，上海 200245；2.上海大学 机电工程与自动化学院，上海 200072)

0 引言

在以客户为中心商业模式中，产品的多样化、客户需求的个性化及严重的同质化现象给客户带来了更加多样性的选择空间，致使大多数制造企业出现客户流失现象，而发展新的客户也极其不易的，使得企业想要生存与发展须采取一定的措施来挽留更多的客户，即企业只需低成本为客户服务，就能使忠诚客户为其他客户选择本企业服务或产品带来积极的效应，进而为企业创造新的交易。对制造业客户历史数据进行深度挖掘，同时发现新的客户群，减少客户群流失显然是十分重要的。有研究表明，一个小客户群保持率的提高有助于企业利润客观的改善，客户流失率减少5%，在不同的行业中，可以使企业利润增加30%～85%。相比于客户挽留，发展一位新客户的成本是挽留一位客户的5～7倍，而保持现有客户的成功率却是发展新客户成功率的16倍[1]。因此如何能够有效地辨别哪些客户是具有潜在流失的客户，哪些客户是忠诚的客户，使得建立产品服务系统客户流失模型是制造企业成功与否的关键。

产品服务系统客户流失状态识别，即客户流失变量到客户流失状态的映射，其决定着产品服务系统方案配置设计是否能精准进行，是提供有效方案给客户，并成功实现客户挽留的前提。识别出产品服务系统客户流失状态，对于辅助设计师对针对性的客户进行产品服务系统方案设计而言，是非常重要的一步。因此，产品服务系统客户流失状态的识别，企业能及早发现未来具有潜在流失行为的客户，并采用有效措施，使客户自身价值得到提升有着重要意义。

为了有效的预测出具有潜在流失行为的客户问题，许多国内外学者应用基于传统统计学方法，如贝叶斯分类器[2-3]、聚类分析[4]、决策树[5-6]、回归[7]等，这些方法对模型的构建具有较强的可解释性，但是其均要求大量的数据，模型对数据训练有一定的难度。而客户流失问题是典型的二分类问题，客户数据往往是高维度的、非线性的，分类结果往往需有较高的准确性，上述模型优越性不能很好的体现。基于人工智能的预测方法，如人工神经网络[8]、支持向量机[9-10]。相对于传统的统计学方法，基于人工智能的预测方法将人工智能因素引入到预测方法中，可获取更高的预测精度，但是神经网络主要是依靠传统的经验风险最小化原则进行建模与预测，在处理小样本时，易导致过度学习，致使泛化能力下降。而支持向量机是一种基于结构风险最小化的机器学习方法，有较强的自适应和学习能力，能克服过拟合现象，其泛化能力强。但是传统的支持向量机在进行模型构建时，其性能受其参数影响较大，要想使客户流失预测模型获得最优的性能，首先需要选择最合适的SVM参数。粒子群算法是一种新兴的优化算法，由于其算法流程简单、参数设置少、收敛速度快等优点[11]，近年来在许多领域都得到了应用，如粒子群算用于优化问题[12]、分类问题[13,14]和规则挖掘问题[15-16]。基于PSO优化SVM的方法已被应用于客户流失预测模型中[17]，但是传统标注PSO优化SVM参数易于陷入局部最优[18]。

鉴于上述分析，为了提高SVM在顾客流失模型中的预测精度，对关键参数的设置与优化非常重要。因此，本文针对客户流失数据的特点和现有算法的不足，构建了一种改进粒子群算法优化支持向量机的产品服务系统客户流失预测模型。

1 支持向量机和改进PSO算法

1.1 支持向量机概述

支持向量机是Cortes等[19]在1995年基于统计学理论提出来的，是一种小样本学习方法，其主要思想是针对二分类问题，在高维度复杂的空间中寻找一个超平面作为两类的分割，以保证最小的分类错误。而客户流失预测问题是一种典型的非线性、高维度的二分类问题。首先，构造训练集为：{(x,y)}，x是输入样本数据，y是样本类别。SVM可将样本通过非线性函数f(x)映射射到高维度空间G，并在高维空间中进行线性回归，其线性回归函数为:

g(x)=w·f(x)+b

(1)

式中，权重向量为w，偏置为b。

根据结构风险最小化原则，可将支持向量机进行估计回归的问题转化为如下优化问题：

(2)

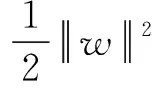
为了进一步简化上述模型，引入拉格朗日函数，将其转化为二次优化问题，则有:

(3)

式中，αi和αi*均为拉格朗日乘子。

则得到的支持向量机预测模型为：

(4)

在进行非线性预测时，最关键的是选择合适的核函数以及确定相对应的参数。常用的核函数有Sigmoid核函数、多项式核函数、径向基核函数等[20]。核函数及其参数通常情况下是通过不断的进行实验，然后经过对比分析的方法获取。但是在大多数情况下，选取径向基核函数进行预测的性能较好，所以本文采用径向基核函数。径向基核函数可表示为：

(5)

产品服务系统客户流失预测模型中的SVM参数优化目标是提高预测准确度，因此采用将预测准确度(T)作为优化目标函数，因此，PSO对SVM参数优化目标函数为：

(6)

模型中参数(C,δ)的选取决定了是否能够精确预测。在通常情况下，将整理好的数据分为两组，其中一组用于训练以保证预测精度，而交叉验证的方法是该方法的改进方法。通过交叉验证的方法搜索到最优的参数(C,δ)，选取精度最高的一组参数作为最优的参数。

则最终的支持向量机的预测模型为：

(7)

1.2 标准粒子群算法

(8)

(9)

1.3 改进的粒子群算法(IPSO)

1.3.1 初始化方式

标准粒子群算法其粒子群初始化位置通常是随机分布的。在搜索空间内，种群初始化位置在一定程度上对算法的寻优效果有影响[21]。因此采用基于Sobol()序列[21]产生均匀随机数的方法初始化粒子群(如图1b),相对于图1 a，图1 b中的点在空间的分布更加均匀，解的多样性更好，这样更容易搜寻到最优解。初始化方式为：

pij=p1jmin+Sobol(i,j)·(p1jmax-p1jmin)

(10)

vij=v1jmin+Sobol(i,j)·(v1jmax-v1jmin)

(11)

p1jmin与p1jmax分别表示粒子群位置的第j维的最小值与最大值，v1jmin与v1jmax分别表示速度最小值与最大值。

(a) 普通随机rand序列点 (b) 基于Sobol的序列点图1 普通随机rand序列与Sobol序列

1.3.2 惯性权重

标准粒子群算法易陷入局部极值和后期容易出现严重的震荡，为了平衡全局搜索能力与局部搜索能力，采用动态惯性权重，在算法初期，设置较大的惯性权重以便在较大范围内搜索，而在算法后期小的权重有利于在精细的局部范围内搜索。本文采用一种惯性权重非线性递减方法，使惯性权重在算法早期下降较慢，算法后期下降较快。非线性权重更新方程为：

(12)

式中，wmax、wmin表示惯性权重的最大值与最小值。wIter表示第Iter代惯性权重值。Iter表示当前迭代次数，maxgen表示最大迭代次数。

2基于IPSO-SVM的产品服务系统客户流失预测模型

产品服务系统客户流失预测的目标是通过发现具有潜在流失行为的客户，采用一定的挽留措施，实现客户挽留率最大化。客户流失预测模型是增强客户忠诚和持久关系的一种重要策略，其实质上是以客户的历史记录数据为基础，对潜在的流失客户状态进行判断的过程。其主要过程：首先从客户历史记录中抽取核心属性，然后通过数据挖掘方法挖掘出具有潜在流失倾向的客户，最后企业根据挖掘出结果，及时制定出具体的挽留策略和价值提升策略，减少客户流失。其中，产品服务系统客户流失预测模型流程如图2所示。

图2 产品服务系统客户流失预测模型流程图

支持向量机中参数优化就是为了找到一组(C,δ)使得准确率值最大，采用改进粒子群算法优化这组参数。IPSO-SVM的客户流失预测模型算法流程如下：

(1)对数据集进行归一化处理，将全部信息映射到[0,1]区间内；

(2)初始化各个输入参数，基于Sobol序列初始化粒子群，每个粒子代表一组参数(C,δ)；

(3)利用SVM进行学习和训练，并通过交叉验证的思想计算目标函数值。更新粒子的位置和速度；

(4)计算每个粒子目标函数值，并更新全局最优解gbest和局部最优解pbest；

(5)如果达到迭代次数，保存全局最优粒子位置，否则转至步骤(3)；

(6)将最优位置对应的SVM参数构建产品服务系统客户流失预测模型。

3 案例研究

3.1 数据来源

为了验证基于IPSO-SVM产品服务系统客户流失模型的可行性，从某数控机床公司在某一时间段内客户流失状况数据进行整理与分析，从客户历史数据中抽取8个核心客户流失影响属性，主轴转速(CR1，r/min)，自动化程度(CR2)，加工范围(CR3，mm)，客户当前是否可联系(CR4)，加工精度(CR5，公差等级)，可靠性(CR6，平均无故障时间(h))，机床本身精度(CR7)，维修人员技术支持(CR8)。初始化数据集中有157个样本(见表1)，从中随机选取90个数据作为训练数据集，其中47位客户在该时间段内客户状态为流失客户，其他客户为非流失客户(正常状态客户)。另外67个样本为测试数据集，其中包含了36个正常状态客户与31个流失客户。企业客户状态为流失客户用1表示，客户状态为非流失客户用2表示。其中，各核心属性的取值范围为CR1∈{500～8000}，CR2∈{低、中、高}，CR3∈{5～20,20～50,50～80,80～100}，CR4∈{N,Y}，CR5∈{6,7,8,…,13}，CR6∈{400～1200}，CR7∈{低、中、高}，CR8∈{N,Y}。为了将上面数据转化为支持向量机能够接受的数据形式，其处理方式为：将CR2及CR7采用{(1 0 0)/(0 1 0)/(0 0 1)}形式表示，CR4及CR8采用{(1 0)/(0 1)}表示。预测流失计算指标矩阵如表2所示。

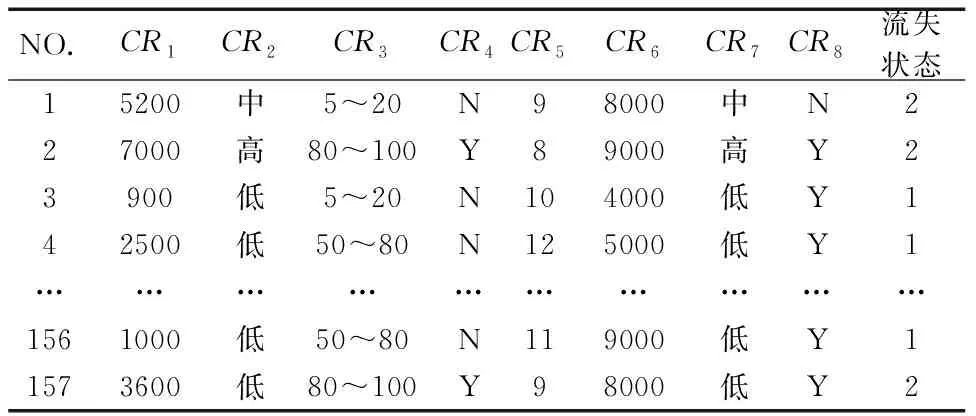
表1 初始数据集

表2 预测流失计算指标矩阵

3.2 评价指标

为了验证所提的IPSO-SVM预测模型的泛化性能，采用BP神经网络(BPNN)、SVM、PSO-SVM模型作为对比模型，模型评价指标为模型准确率、命中率、覆盖率与提升系数。其中，模型评价标准由预测流失计算指标矩阵获得。并有如下定义：

(13)

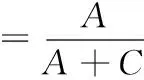
(14)

(15)

(16)

3.3 算法参数选取

针对所构建的模型，设置BPNN网络隐含层结构为23-10-2。粒子群算法种群规模N=30，c1=c2=2，算法最大迭代次数为200代，wmin=0.4，wmax=0.9。PSO及IPSO算法优化参数(C,δ)的取值范围为0.01≤C≤100,0.01≤σ≤1000。

3.4 结果对比与分析

采用BPNN、SVM、PSO-SVM及IPSO-SVM算法对数控机床产品服务系统客户流失状态进行预测结果如图3所示。从图3预测结果可以得到如下结论：

相对于BPNN模型，SVM的预测准确率、命中率、覆盖率及提升系数均有所提高，这说明SVM能够改善BP神经网络过拟合现象。相对于SVM模型，PSO-SVM、IPSO-SVM的预测准确率都有所提高，表明粒子群算法在进行支持向量机的参数优化后，能够克服基于网格搜索算法的难以找到SVM最优参数的缺陷，降低了产品服务系统客户流失的预测误差，提高了预测准确度。相对与BPNN、SVM及PSO-SVM模型，基于IPSO-SVM的产品服务系统客户流失预测结果更加理想，这是由于SVM能够更好的克服BPNN过拟合现象，而IPSO-SVM比PSO-SVM预测结果更好，是由于改进的粒子群算法能够更好地避免算法陷入局部最优值，因此基于改进的粒子群算法优化支持向量机比标准支持向量机及标准粒子群优化支持向量机在产品服务系统客户流失状态预测问题上具有更好的性能。

图3 产品服务系统客户流失状态预测性能对比

4 结束语

SVM在进行产品服务系统客户流失预测过程中，如果其参数选取不合理，直接影响着客户流失预测模型的准确度。为了提高产品服务系统客户流失预测模型中预测精度，提出了一种改进的粒子群算法与支持向量机集成的智能化学习方法。首先，采用支持向量机在处理小样本、高维度、非线性数据条件下分类具有较高准确度的优势，建立了改进粒子群算法优化支持向量机的客户流失预测模型(IPSO-SVM)。将该模型应用于某高档数控机床产品服务系统的客户流失中，通过与BPNN、SVM、PSO-SVM对比，验证了所提方法具有较强的泛化能力及拟合精度，有助于精准地为潜在流失客户提供具体的产品服务系统方案。

[参考文献]

[1] Reichheld F F, Jr S W. Zero defections: quality comes to services.[J]. Harvard Business Review, 1990, 68(5):105.

[2] Sun P, Guo X, Zhang Y, et al. Analytical Model of Customer Churn Based on Bayesian Network[C]// International Conference on Computational Intelligence and Security, IEEE, 2013:269-271.

[3] Verbraken T, Verbeke W, Baesens B. Profit optimizing customer churn prediction with Bayesian network classifiers[J]. Intelligent Data Analysis, 2014, 18(18):3-24.

[4] 王颖, 陈治平. 结合K-means的分类方法在电信客户流失中的应用[J]. 佳木斯大学学报(自然科学版), 2010, 28(2):175-179.

[5] Luo B, Shao P, Liu J. Customer Churn Prediction Based on the Decision Tree in Personal Handyphone System Service[C]// International Conference on Service Systems and Service Management, IEEE Xplore, 2007:1-5.

[6] 林芳. 基于决策树的客户流失模型的建立[J]. 赤峰学院学报(自然版), 2016, 32(21):18-19.

[7] Mohammadi G, Tavakkolimoghaddam R, Mohammadi M. Hierarchical Neural Regression Models for Customer Churn Prediction[J]. Journal of Engineering, 2013, 2013(23):1-9.

[8] Tsai C F, Lu Y H. Customer churn prediction by hybrid neural networks[J]. Expert Systems with Applications An International Journal, 2009, 36(10):12547-12553.

[9] 赵宇, 李兵, 李秀,等. 基于改进支持向量机的客户流失分析研究[J]. 计算机集成制造系统, 2007, 13(1):202-207.

[10] 王观玉, 郭勇. 支持向量机在电信客户流失预测中的应用研究[J]. 计算机仿真, 2011, 28(4):115-118.

[11] Nissen V, Günther M. Application of Particle Swarm Optimization to the British Telecom Workforce Scheduling Problem[C]// Int. Conference on the Practice and Theory of Automated Timetabling, Sintef, Trondheim. 2012.

[12] Chen D, Chen J, Jiang H, et al. An improved PSO algorithm based on particle exploration for function optimization and the modeling of chaotic systems[J]. Soft Computing, 2015, 19(11):3071-3081.

[13] Das H, Jena A K, Nayak J, et al. A Novel PSO Based Back Propagation Learning-MLP (PSO-BP-MLP) for Classification[J]. 2015,2:461-471.

[14] 张伟, 师奕兵, 周龙甫,等. 基于改进粒子群算法的小波神经网络分类器[J]. 仪器仪表学报, 2010, 31(10):2203-2209.

[15] Beiranvand V, Mobasher-Kashani M, Abu Bakar A. Multi-objective PSO algorithm for mining numerical association rules without a priori discretization[J]. Expert Systems with Applications, 2014, 41(9):4259-4273.

[16] 刘园, 张在房, 姚迪,等. 基于多目标离散粒子群的产品服务系统方案配置规则提取[J]. 上海交通大学学报, 2015, 49(8):1123-1130.

[17] 卓涛. 基于粒子群优化支持向量机的电子商务客户流失预测模型[J]. 农业网络信息, 2014(6): 88-91.

[18] 鞠秋文. PSO-SVM算法在网络入侵检测中的研究[J]. 计算机仿真, 2011, 28(4): 130-132.

[19] Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3):273-297.

[20] 王姣, 刘海燕. 基于支持向量机和遗传算法的刀具故障诊断[J]. 组合机床与自动化加工技术, 2013(1): 74-76.

[21] Joe S, Kuo F Y. Constructing Sobol Sequences with Better Two-Dimensional Projections[J]. Siam Journal on Scientific Computing, 2008, 30(5):2635-2654.