初中数学教学中数形结合思想的渗透

林慧

【摘要】在数学教学过程中，有机结合数与形，可以有效转换抽象思维，并形成形象式思维，进而在不同程度上揭露数学教学本质，大大降低数学知识学习难度，有助于提高学生学习水平.

【关键词】初中数学；数形结合；思想渗透

初中数学教学过程中，应用数学结合思想就是结合数学教学中的各项知识内容，让学生可以将形象与抽象思维有效结合，从而实施两者转化性学习，让抽象概念能够转变成较为具体化的图形.为了可以对数形结合思想更加清晰地了解，本文研究了函数中与应用题中“数学结合”思想的差异，希望能够提高初中学生的数学学习能力.

一、初中数学函数中渗透“数形结合”思想

数形结合具有众多优势，它能够让抽象的函数与直观图形之间实现双向联系，达到化抽象为形象的目的.在初中数学知识学习中，由于一般二次函数问题是十分抽象的，在学习中，由于这部分知识学起来有些困难，学生不愿意学习与二次函数有关的数学题.由于二次函数有其自身特征，因此，同函数图形之间有着密切的联系，初中生只要是在直角坐标系下，就能够找到函数关键之处，在定位下来做图形，这样问题分析也就会变得更加形象化.从理论层面上分析，在y=ax2+bx+c二次函数中，参数a决定着开口方向，c决定了与y轴的交点，而a和b共同决定了二次函数图形的对称性.因此，若是在学习二次函数过程中使用数形融合的思想，就能够妥善帮助学生处理这一实际问题.如，已知（-1，y1），（-3，y2），（2，y3）在二次函数y=3x2+6x+2图像中，对y1，y2，y3的大小关系进行判断.分析：此题是对二次函数大小进行判断，若是初中生不知如何运用数形结合思想，就肯定会在二次函数中将每一个点的x值代入，

然后在将y值求出，这样计算的话，不但计算量非常大，而且学生还可能会在计算中出现错误.但若是学生能够运用数形结合思想做出来y=3x2+6x+2图形，就能够对y1，y2，y3之间大小关系进行对比.如右图所示为y=3x2+6x+2简图.

二、运用数形结合思想可以简化应用题学习

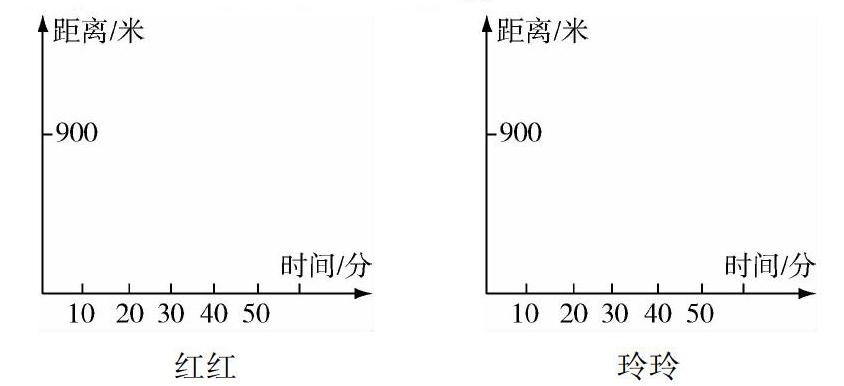
在初中数学知识学习中，不可避免要学习到应用题知识，并且在初中时期的应用题是十分有难度的，很多初中生计算半天也很难计算出准确答案.如，在“一元一次方程”学习中，教学者应带领学习者阅读应用题题目，从已知条件中得到题目中已给的条件，并分析每个要素间的关系.同时，在学习中能够采用坐标系的方式来将函数图像画出来，在对函数图像分析中，学生能够快速地、有效地得出最终结果，从而简化了整道应用题.如，红红与玲玲相约一同出去游玩，早上八点两人一同出发，走了30分钟后遇到一片绿草地，此草地距离家有900 m，紅红玩了一段时间之后就不想玩了，便保持之前的速度赶回家了，玲玲在草地玩了15分钟之后也走回家了，回到家后共花了20分钟.结合这一段描述，可以在下面的平面直角坐标系中准确描述出红红与玲玲离家时间和距离的关系吗？

红红

玲玲

对于这种类型的数学习题在初中数学知识学习中经常遇见，也是一类较为基础型的数学习题.若是这种类型习题出现后，教学者引导学习者从日常生活中入手，并运用数学结合思想妥善解决这一问题.其中，结合题目中给出的信息，可选择x，y两个未知数表示距离以及时间，并表示好二者之间的关系.这样一来，在不断练习中，不但能够加强学生对数轴知识的认识，而且也可以为学生日后学习这种类型的知识打下坚实基础.

三、在数学概念学习中数形结合思想的有效应用

在数学知识学习过程中，数学概念是一项基础的知识，对于引导学生深入学习数学知识有着很大的影响.在初中数学概念教学过程中，数形结合思想的应用，可以促使学生对数学概念知识更加有效地了解.在数学知识学习中，有很多概念都是抽象的，加大了进行课程教学活动的难度.数学教师可利用图形方式讲解这些知识，提高初中学生整体上掌握数学概念的能力.如，在引导学生对对称轴知识学习中，教师能够在对折某个图形中，而后引导学生对直线两边图形特征进行观察，在数学教师对折后重叠了图形，直线两边图形也可以完全重合.教学者在带领学生观察和分析的前提下，引导学习者主动思考，并讲出折叠之后图形的特征，然后讲出对称轴的概念，使学生能够轻松的、容易的掌握这节数学知识.

四、结 语

在初中数学课程教学过程中，应用数形结合思想有利于实现有效结合理论知识以及图像表达，从而实现有效融合知识引导与思维培养，教师能够根据学生认知特征，对数学结合思想巧妙的、形象的应用，确保学生可以对解答数学习题技巧更好地掌握，进而可以对数学知识更加轻松的学习，形成一定的数学思维.

【参考文献】

[1]侯招琴.数形结合思想在高中数学教学中的有效运用[J].吉林教育，2017（31）：80.

[2]茅春娟.初中数学教学中数形结合思想的实践探析[J].文理导航（中旬），2017（8）：28.