VAR模型在我国货币供应量预测中的应用

王艳，张碧霞

（1.武汉理工大学，湖北武汉430070；2.中南民族大学，湖北武汉，430074）

货币供应量是国民经济中的一个重要指标，对宏观经济运行具有重要的影响。货币供应量与经济发展有着密切的关系，它同收入、消费、投资、价格、国际收支等经济活动直接相关。货币供应量与GDP更是联系紧密，通常情况下，货币供应量越充足，预示着消费和投资活动越旺盛，随之推动GDP的增长，而GDP的增长又加速了社会财富的积累，带动货币供应量的增长，同时引发新一轮的消费、投资热潮，进一步刺激经济的增长。如此循环，如果货币供应量与经济的发展协调一致，将不断推动经济的持续发展。可见，合理的货币供应量增速，对经济的发展具有积极作用。在货币供应量3个指标中，M1和M2对经济的波动和价格的波动较为敏感，如果M1增速过快，则会引起消费和终端市场活跃，容易出现通货膨胀，如果M2增速过快，则导致投资和中间市场活跃，容易出现资产泡沫。因此，为了保持社会总需求和总供给的平衡，货币供应量应当适度。研究M1和M2的变化发展趋势，是制定宏观经济政策的基础，对防止经济出现大起大落，保持国民经济健康发展具有重要意义。国内有许多学者对我国货币供应量进行过预测，但大多针对一个指标而言，M1或是 M2［1］［2］［3］［4］，对M1和 M2组合预测的研究还不多见，将二者联系在一起研究对分析我国宏观经济更有价值。向量自回归模型（VAR）是用于对多个相关联的时间序列进行预测的模型，能够刻画变量之间的联系和影响，建模逻辑严密，推理充分，涵盖的信息量广，预测精度高，在经济领域得到了广泛应用。本文运用VAR模型预测我国货币供应量M1和M2的变化趋势。

一、VAR模型预测方法

（一）VAR模型基本形式

VAR模型常用于对2个或多个相关联的时间系列的预测，VAR模型一般可表示为［5］［6］：

式中，yt为n维内生向量；xt为M维外生向量；εt为n维随机扰动向量；Ai（i=1，2，…，p）和 B 为系数矩阵。

式（1）称为限制性向量自回归模型。

特别地，当外生向量为常数矩阵 C 时，VAR 模型变为［5］［6］：

式（2）称为非限制性向量自回归模型。

（二）VAR模型预测方法与步骤

1.单位根检验

单位根检验的目标是检验系列中是否存在单位根，如果序列中存在单位根，表明系统是非平稳序列，一般采用ADF检验（加强迪基-福勒检验）进行判断，主要通过考察t统计量的值大小确定是否有单位根，如果t值小于1%、5%、10%的显著水平下的临界值，则说明序列是平稳的，否则，则需要对序列进行差分或对数变换，直至其变为平稳序列。满足的显著水平越小，系列越平稳，3个显著水平不一定都要满足，一般只要满足5%的显著水平下的临界值即可。

2.模型滞后阶数确定

VAR模型最关键的一个参数就是滞后期p。足够大的p能够较为完整地反映所构造模型的动态关系信息，但滞后阶数越大，模型的自由度就越小。因此，需要权衡滞后期和自由度之间的关系，在两者之间寻找出一种均衡的最佳状态。VAR模型的滞后阶数p一般根据AIC准则（赤池信息准则）和SC准则（施瓦兹准则）来确定，即AIC和SC最小值的阶数为最佳滞后期p，如果AIC和SC不是同时取值最小，则采用LR检验（似然比检验）进一步确定，LR最大的滞后阶为最佳滞后阶。若VAR模型滞后阶数为p，则称为p阶VAR模型，记为 VAR（p）。

3.协整性检验

协整性检验是检验变量之间是否存在长期稳定的关系。也就是变量之间是否存在共同的随机性趋势。协整性检验一般采用约翰森检验（Johansen Test）方法。主要考察迹统计量 （Trace Statistic）和似然概率（likelihood probability），若迹统计量小于显著水平的临界值（一般为5%），似然概率大于显著水平（一般为5%），则变量之间存在协整关系。

4.格兰杰检验

格兰杰检验（Granger Test）主要考察变量的先后影响联系，即检验一个变量及其滞后期对另一变量的影响关系。因此，格兰杰检验的因果关系并非我们通常理解的因果的关系，而是说一个变量前期变化能有效地解释另一个变量的变化，是统计意义上的“格兰杰因果性“，不能作为衡量变量之间是否存在因果关系的依据。设有2个变量x、y，如果变量x信息的加入对预测变量y的效果优于单独用变量y自身的信息预测的效果，即变量x有助于解释变量y的将来变化，则认为变量 x是导致变量 y的格兰杰原因［7］［8］。

5.参数估计

滞后阶数确定后，建立VAR（p）模型，根据选定的模型估计参数 Ai（i=1，2，…，p）和 B。通常采用最小二乘估计的方法来估计模型参数，它可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小，属于最佳线性无偏估计。

6.模型的稳健性检验

模型的参数确定后，还须对模型进行稳健性检验。如果模型的所有特征根的倒数都小于1，即位于单位圆内，说明模型的结构是稳定和显著的，这样可以保证脉冲响应函数和方差分解的有效性，此时才可根据模型估计参数建立预测参数方程，对向量组时间序列的变换发展趋势进行判断。

7.脉冲响应分析

脉冲响应函数主要用于考察一个变量受到其它变量冲击所带来的影响，是系统一个内生变化对某一变量扰动的一个冲击所做出的动态反应，即在随机误差项上施加上一个标准差大小的冲击后，对变量当期和未来期的值的影响程度。通过比较不同变量对于误差冲击的动态反应，可以考察变量之间的动态关系。

8.方差分解

方差分解是考察系统中各变量对某一变量预测方差的贡献度大小，进一步评价不同结构的冲击的重要性，即将VAR系统内一个变量的方差分解到各个扰动项上，以分析系统内各变量对变量预测方差的影响程度。

二、我国货币供应量预测

（一）VAR模型变量的选取

图1为2016年1月—2017年11月我国货币供应量M1、M2的统计数据，在23个月中，我国货币供应量M1、M2虽有所波动，但整体呈上升态势，M1和M2均在稳步增加，表明我国宏观经济整体运行平稳，势态向好。将我国货币供应量M1、M2组成二维向量时间序列Y=（M1，M2），以23个月Y序列数据为样本，然后建立VAR预测模型。

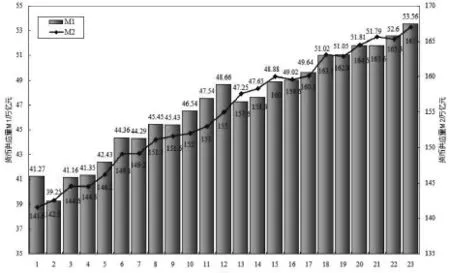
图1 我国货币供应量统计数据

（二）单位根检验

从图1可知，M1和M2既有波动又有趋势性，并非为平稳时间系列，通过单位根检验可以明确判断，单位根检验见表1。从表1知，M1的ADF值为-0.263780，大于1%、5%、10%临界值，M2的ADF值为-2.01101，也大于1%、5%、10%临界值，验证了 M1、M2均是非平稳时间序列，且M1更为不平稳。对M1、M2进行一次差分，差分后 d（M1）的 ADF 值为-8.340660，小于 1%、5%、10%临界值，即转化为平稳时间系列，d（M2）的 ADF值为-4.040214，小于1%、5%、10%临界值，也转化为平稳时间序列，这种经过一次差分后转化为平稳系列，称为 M1、M2为一阶单整，它满足以下各种检验和建模的条件。

表1 单位根检验结果

建立向量自回归模型，模型初步定为 VAR（2），以检验 d（M1）、d（M2）协整性、格兰杰因果关系，并确定模型的最佳滞后期。

（三）协整性检验

对 d（M1）、d（M2）进行协整性检验，结果如表 2。从表 2 知，对于原假设无协整性，迹统计量14.93407，大于5%的临界值12.32090，似然概率为0.0179，小于0.05，故拒绝原假设；对于最多一个协整关系，迹统计量2.108372，小于5%的临界值4.129906，似然概率为0.17.27，大于0.05，故接受原假设，说明二者存在长期一致的变化趋势，在考察期内，d（M1）、d（M2）都保持稳定增长态势说明了这一点。

表2 协整性检验结果

（四）格兰杰检验

对 d（M1）、d（M2）进行格兰杰检验，结果如表 3。 从表 3 知，对于原假设“d（M2）不是d（M1）的格兰杰原因”，在 5%的置信水平上，统计量 F的概率为0.0434，小于 0.05 的显著水平，故拒绝原假设，即 d（M2）是 d（M1）的格兰杰原因，说明M1受企事业单位定期存款和居民储蓄影响较小；对于原假设“d（M1）不是d（M2）的格兰杰原因”，在5%的置信水平上，统计量F的概率为0.6571，大于0.05的显著水平，故接受原假设，即d（M1）不是d（M2）的格兰杰原因，这说明M2受企事业单位定期存款和居民储蓄影响较大，并且它们存在很大的不确定性。

表3 格兰杰检验结果

（五）模型滞后阶数确定

模型滞后阶分析结果如表4。从表4知，在考察的5个滞后阶中，在5%的置信水平下，滞后1阶的AIC=5.283608，SC=5.382535，均为所考察阶数中值最小（带*号），LR=5.962843，为所考察阶数中值最大（带*号），故模型最合适的滞后阶为p=1，因此，模型最后确定为VAR（1）。

表4 模型滞后阶分析结果

（六）参数估计

建立VAR（1）模型，对模型的参数进行估计，结果如表5。其中，参数第一项为系数，第二项为标准差（带小括号），第三项为t统计量（带中括号）。对所建的VAR（1）模进行稳健性检验，结果如图2。从图2知，模型的两个特征根都没有超出单位圆，说明模型是稳固和有效的，可以用于预测。因此，根据估计的参数可得到如式（3）的预测方程，即我国货币供应量M1、M2的预测方程式。

表5 模型的参数估计结果

图2 模型的稳健性检验结果

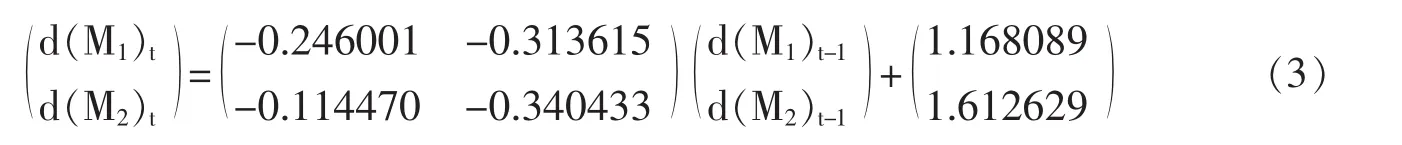
（七）脉冲响应分析

图3为d（M1）和d（M2）相互冲击扰动对彼此之间的影响。从图 3知，d（M2）的冲击扰动引起d（M1）脉冲响应开始较大，随着滞后期的延长，逐步减弱最后收敛于0。d（M1）冲击扰动引起自身脉冲响应相对较小，并随着滞后期的延长，慢慢减弱，最后趋于0；d（M2）冲击扰动引起自身脉冲响应比较大，开始震荡很强烈，最后也消退为0，d（M1）的冲击扰动引起d（M2）脉冲响应较小，随着滞后期的延长，震荡衰减稳定在0，这些都说明误差扰动对模型的影响是稳定的。

（八）方差分解

d（M1）和 d（M2）的方差分解结果如图 5。 从图 5 知，d（M1）方差主要来自自身，贡献率大约 80%左右，后期比较稳定，几乎为直线，d（M2）对 d（M1）方差影响要小，贡献率大约为20%，后期也比较稳定；d（M2）方差也主要来自自身，贡献率为95%左右，影响也比较稳定，几乎为直线，d（M1）对d（M2）的方差的贡献率仅为5%左右，影响很稳定。以上分析说明，M1和M2预测精度都主要取决于自身内部信息。

图4 方差分解结果

（九）模型预测

根据预测方程（3）对我国货币供应量M1和M2进行预测，结果如表6（由于篇幅所限只列出最近10个月的预测值）。从表6可知，模型对M1预测的平均预测误差为0.8622%，对M2预测的平均预测误差为0.4743%%，都小于1%，显示了运用VAR模型预测我国货币供应量M1和M2的可行性和可靠性，预测曲线如图5和图6，由模型预测得到2017年12月我国货币供应量M1和M2分别为53.95878万亿元和167.9240万亿元。

表6 模型预测结果及比较

图5 我国货币供应量M1预测曲线及对比

图6 我国货币供应量M2预测曲线及对比

三、结 语

科学预测我国货币供应量变化规律，对维护社会供给平衡，防止经济出现过冷过热，提高经济发展质量和速度，保持物价相对稳定，维护社会和谐稳定，促进经济持续健康发展等具有重要的意义。文中采用VAR模型对我国货币供应量M1和M2进行预测，取得了满意的效果，对M1预测的平均预测误差为0.8622%，对M2预测的平均预测误差为0.4743%，由模型预测得到2017年12月我国货币供应量M1和M2分别为53.95878万亿元和167.9240万亿元。

参考文献：

［1］谢宇睛.货币供应量 M2 预测精度：基于组合模型的改进［J］.统计与决策，2017，（5）：93-97.

［2］郇志坚，徐晓莉，我国货币供应量预测：基于 STM 模型［J］.金融理沦与实践，2016，（11）：46-48.

［3］刘畅.我国狭义货币供应量M1的预测与分析——基于ARIMA模型与回归模型［J］.中国证券期货，2011，（12）：162-163.

［4］乔毅红，方晶晶.2010-2019中国国内生产总值与广义货币供应量的预测［J］.管理现代化，2010，（4）：45-47.

［5］舒服华，杨桂山.基于VAR的中国仓储指数与中国物流业景气指数预测［J］.唐山学院学报，2017，30（6）：62-67.

［6］万礼，杨呈佳，吴全志.基于VAR模型的贵州省经济增长与金融发展关系的实证研究［J］.中国集体经济.2017，（12）：63-65.

［7］谷秀娟，何青畔.基于VAR模型的我国存贷款利差与房地产开发投资影响分析［J］.产业与科技论坛.2016， 15（24）： 85-91.

［8］万礼，杨呈佳，吴全志.基于VAR模型的贵州省经济增长与金融发展关系的实证研究［J］.中国集体经济.2017，（12）：63-65.