一种新的多址信道有效阶数估计算法*
2014-09-28李双志张建康穆晓敏
李双志,张 喆,张建康,穆晓敏
(郑州大学 信息工程学院,郑州450001)
1 引言
多用户OFDM/SDMA通信机制整合了多输入多输出(Multiple-Input Multiple-Output,MIMO)和正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)两种技术优势,在抗多径衰落及提高带宽效率和可靠性方面具有巨大潜力,是未来宽带无线通信领域的关键技术。基于MIMO的空分多址接入(Space Division Multiple Access,SDMA)技术作为提高移动通信系统容量的有效手段,已成为近年来该领域的研究热点。准确的信道状态信息是MIMO-OFDM系统多用户检测、空时解码等的必要条件,因此信道估计的准确性将影响系统的整体性能。
基于时域的信道估计方法[1-3]通常将信道建模为有限长脉冲响应滤波器,忽略幅度较小的信道链路能够降低系统计算复杂度和提高信道估计的精度[1]。已有文献[4]证明,假设信道有效阶数与实际有效阶数的偏差会影响信道估计性能,偏差估计精度越高,对噪声和信道间干扰的鲁棒性越好。文献[5]指出了信道有效阶数与信噪比和实际信道阶数有关,因此应当自适应选择信道有效阶数,使它接近最优值。在OFDM系统中,解决该问题的一个较简单方案就是假设信道有效阶数为保证不产生子载波和符号间干扰的信道阶数最大值,即OFDM循环前缀(Cyclic Prefix,CP)长度加1。这种假设虽然简化了问题,但在实际信道阶数较低的情况下将导致信道估计器性能的显著下降。文献[6]从信道最大阶数出发,逆向搜索,忽略幅度小于一定阈值的信道抽头来确定信道有效阶数,但该算法对阈值的选取敏感。应用赤池信息量准则(Akaike's Information Criterion,AIC)[7]确定信道有效阶数时,不需要进行阈值设计,以极小化AIC值来确定信道有效阶数[8-9]。
在文献[8]中,AIC应用于信道估计中旨在最小化信道估计器造成的信息损失。直接应用AIC准则来进行信道有效阶数估计,需要进行多次信道估计、FFT/IFFT运算和欧氏距离的计算,限制了其在实际通信中的应用。为此,寻求一种算法结构简单、相对计算量小、实际应用方便的信道定阶方法是很有必要的。文献[9]研究了基于AIC对单输入单输出OFDM系统信道阶数估计算法,并构建Levinson递推算法降低运算量,具有较高的鲁棒性。在多用户OFDM/SDMA系统中,假设链路特性互异的多个移动用户联合构成输入端,各用户的发送信号经历相互独立的信道,链路的信道有效阶数各不相同,它们在接收天线处混叠后等效为一个统一的混合信道矩阵,此时必须同时获得所有用户的信道有效阶数才能使最大似然(Maximum Likelihood,ML)信道估计器达到最佳的估计性能。因此,如何同时对多址信道有效阶数进行有效且快速的估计是一个重大挑战。本文针对多用户OFDM/SDMA系统,以差分进化(Differential Evolution,DE)算法为辅助,提出了基于AIC准则的信道有效阶数并行搜索算法。构建基于AIC准则的多用户信道有效阶数和信道冲激响应(Channel Impulse Response,CIR)的目标函数作为DE算法的适应度函数,然后利用DE在多址信道空间并行搜索有效阶数,并进行CIR估计。仿真结果表明,该算法可以较好估计CIR有效阶数,提高时域ML信道估计器性能。
2 系统模型
假设U个单天线用户联合构成输入端,基站处使用Q根接收天线的多用户OFDM/SDMA上行链路系统。第 q根接收天线处第 s个 OFDM符号为Yq[s](q=1,…,Q)可表示为不同用户接收信号与AWGN的叠加,即
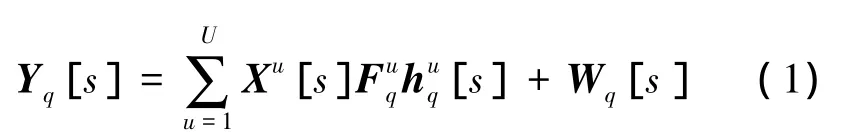
式中,Xu[s]∈CK×K为对角阵,表示第 s个 OFDM 符号周期内用户u(u=1,2,…,U)的频域发送信号,其对角线上元素为 Xu[s,k],k=1,2,…,K,K 为子载波个数为用户u到为F的前列,即

从式(2)中可以看出,Fuq的维数随着多址用户的信道有效阶数变化,因此文献[1]提出的ML信道估计算法具有一定的局限性。文献[2]中提出一种空间交替的广义期望最大化算法,能够把多天线发射信道分解为若干单发送-接收天线对的参数估计问题,避免了文献[1]中ML估计过程中的矩阵求逆运算,最终得到信道冲激响应的ML解。因此本文将采用该算法对信道有效阶数互异的多址信道进行估计。
3 多址信道有效阶数和CIR联合估计算法
在AWGN情形下,时域CIR的ML估计[3]可以表示为

本文基于式(3)提出一种新的多址信道有效阶接收天线 q信道阶数)和Wq[s]∈CK×1分别为频域接收信号 Yq[s,k]、信道冲激响应 huq[s,l]以及AWGN wq[s,k]的列向量表示;wq[s,k]满足均值为0、协方差为σ2n的高斯分布;F∈CK×K为DFT变换矩阵数和CIR联合估计框架,算法的基本思想是利用DE并行搜索信道有效阶数并联合迭代进行CIR估计,并在DE迭代过程中引入AIC准则进行定阶,最终得出多址信道有效阶数及CIR的ML估计。
3.1 基于AIC的定阶算法描述
赤池弘次(H.Akaike)在文献[7]中提出了AIC准则,用于在有限集中选择最佳模型。

在接收天线q处,根据文献[9],可建立多用户系统的信道有效阶数估计问题为
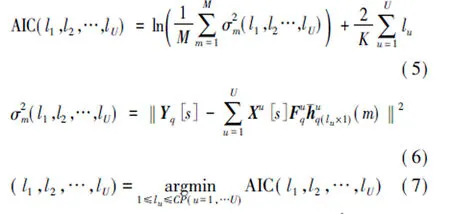
其中,M为发射端做导频的序列个数,σ2m是接收端第m个OFDM符号的残差平方和。对多址信道有效阶数进行遍历性搜索时,需要进行CPU次CIR最大似然估计,其中CP为OFDM符号的循环前缀长度,计算量大,操作复杂,限制了其在实际中的应用。
3.2 基于DE的联合估计算法实现步骤
DE算法是一种基于群体智能理论的全局算法,是通过群体之间的合作和竞争,产生群体智能理论的全局算法,具有较强的全局收敛能力和鲁棒性[10]。DE算法主要由初始化、变异、交叉和选择4个基本操作表征,算法步骤如下,算法流程图见图1。
(1)初始化
利用Np个维数为U的信道有效阶数向量作为每一代的种群,U为用户数,t表示进化代数,i为种群中个体的标号。初始化时,种群中的每个个体在解空间内随机产生。「·?为上取整操作。

其中,BU和BL分别表示解空间搜索上界和下界,BL=1,BU=CP。rand(0,1)表示在(0,1)区间内均匀分布的随机数。
(2)变异
随机选取两个个体,并以它们的差分来扰动第三个随机选取的向量,判断边界条件(步骤1和步骤2),得到变异个体Lv(t+1)i:
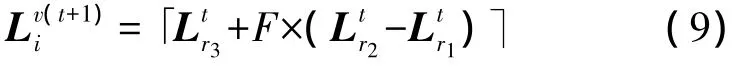
其中,变异因子 F 在区间(0,1)内均匀分布,r1,r2,r3∈{1,2,…,Np}互不相同,并且与标号i也不相同。
(3)交叉
通过式(10)的交叉操作生成试验个体Lu(t+1)i
来增加种群的多样性。randj(0,1)∈[0,1]为均匀分布的随机数。

其中,CR 为交叉因子,randn(i)∈[1,2,…,U]为随机选择的维数变量索引。
(4)选择
按式(11)进行选择操作,生成t+1代个体Lt+1i,进入下一代进化。
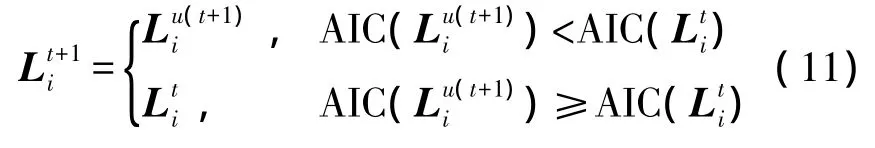
上述过程反复迭代,直到DE算法终止条件得到满足。终止时最优即为信道有效阶数估计值,计算 AIC时与对应的CIR估计值即为CIR的ML估计。
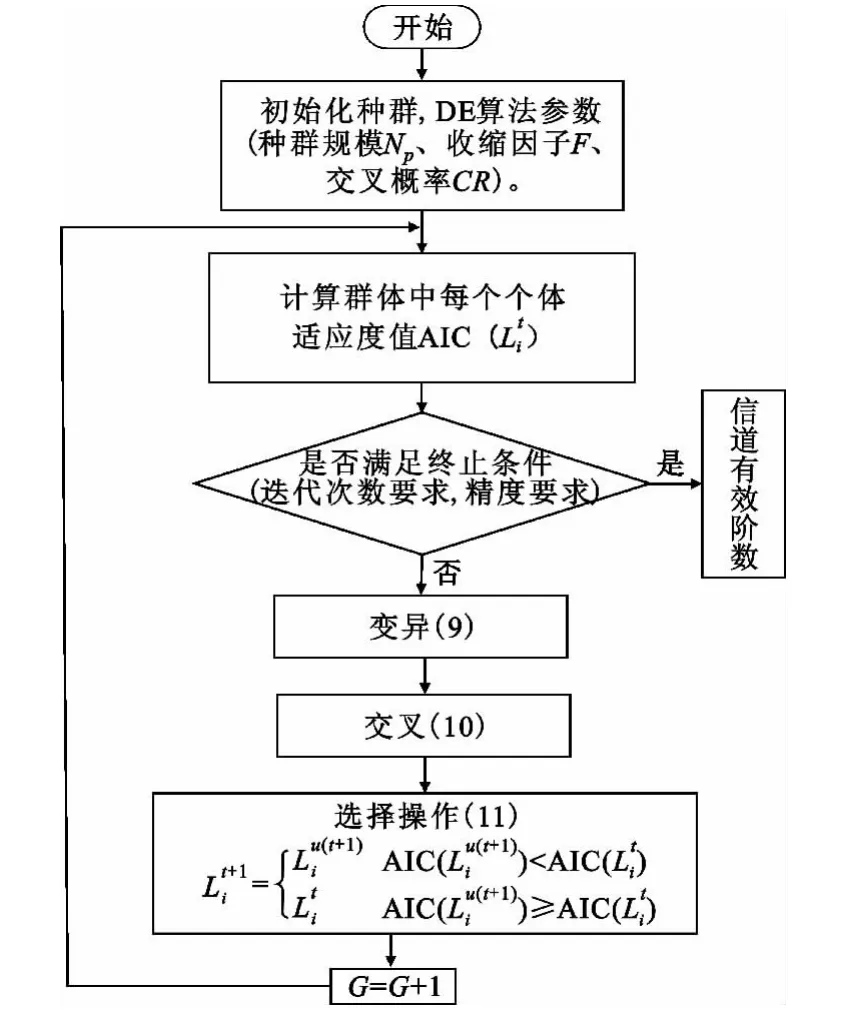
图1 本文所提基于DE的联合算法流程图Fig.1 The flowchart of the proposed joint algorithm based on DE
4 仿真分析
为评估所提算法的估计性能,本文考虑2×2 OFDM/SDMA系统。参照 IEEE802.11n WLAN的参数设置,每个用户所采用的子载波个数K=64,循环前缀长度CP=16。每帧的前两个OFDM符号(M=2)为导频序列,用于搜索信道有效阶数和CIR估计。在实际的通信系统中,不同的用户可以采用不同的调制方式,为了简化设定所有用户采用4-QAM调制。信道模型采用多径瑞利衰落信道模型,各径的幅度衰落服从指数衰落,相位偏移在[0,2π]内均匀分布。DE操作中,种群规模NP=20,变异因子F=0.1,交叉因子CR=0.1。定义归一化均方误差函数(Normalized Mean Square Error,NMSE)表达式为

4.1 DE算法搜索性能
图2为DE搜索算法性能曲线,纵坐标表示DE算法估计多用户CIR有效阶数为该阶的概率。从图中可以看出,随着信噪比的增加,信道有效阶数收敛于实际信道阶数,在Eb/N0=30 dB时,收敛到实际信道阶数的概率近90%。这是因为随着信噪比的增加,信道各链路信号功率大于噪声功率的概率增加,从而使得它们成为有效信道阶数。具有不同信道阶数的发送用户在相同的发射信噪比下,信道阶数较小的用户信道各链路的信号功率大于噪声功率的概率较大,实际信道阶数更易成为有效阶数,因此被检测到的概率更大。
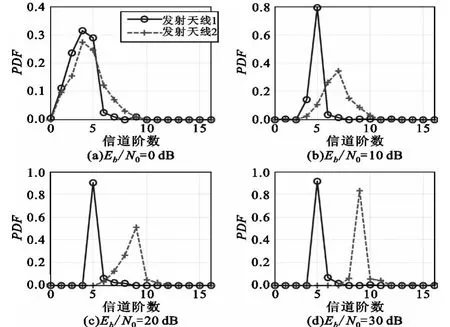
图2 不同Eb/N0下DE搜索算法性能Fig.2 The search performance of DE algorithmunder different Eb/N0
4.2 系统NMSE和误比特率性能
图3 为不同信噪比下使用本文所提算法进行信道估计的NMSE性能曲线,用户实际信道阶数随机产生。通过比较可以看出,低信噪比时,基于本文所提算法估计得到信道有效阶数,信道估计NMSE性能最优;随着信噪比的增加,趋近基于实际信道阶数下的NMSE性能。与采用固定信道阶数的方案相比,本文所提算法能获得约4.5 dB的性能提升。这是因为本文所提算法以信道有效阶数为基准,在低信噪比时,忽略噪声功率较大的实际信道链路,能够更好地抑制噪声干扰,改善信道估计的NMSE性能。在高信噪比时,信道有效阶数收敛于实际信道阶数,信道估计性能收敛于实际信道阶数下的NMSE性能。图4给出了上述3种方案下系统误比特率(Bit Error Rate,BER)性能的比较。从仿真结果可以看出,本文所提算法能够有效地改善系统的信道估计性能。BER=10-5时,与固定信道阶数的方案相比,本文所提算法能够获得约1.5 dB的性能增益。

图3 不同定阶方法下发射用户NMSE性能Fig.3 The NMSE of transmitting users under different order determination scheme

图4 不同定阶方法下多用户OFDM/SDMA系统BER性能曲线Fig.4 The BER performance of multi-user OFDM/SDMA system under different order determination scheme
5 结论
本文在分析多用户OFDM/SDMA系统多址信道时域ML信道估计算法对信道有效阶数存在依赖性的基础上,提出了一种新的多址信道有效阶数估计算法。该算法从实际通信环境出发,考虑多址用户信道链路特性的互异性,引入AIC准则作为搜索最优阶数的评价准则,以提高信道有效阶数和CIR
的估计精度;构建了基于DE算法并行搜索信道有效阶数并进行CIR估计的联合框架,以提高搜索速度。仿真结果表明,该方案能够有效估计信道有效阶数,提高系统的ML信道估计精度,改善估计器性能,降低系统的误比特率。与传统基于固定信道阶数的方案相比,BER=10-5时,本文所提算法能够获得约1.5 dB的性能增益。
[1]Li Y,Seshadri N,Ariyavisitakul S.Channel estimation for OFDM systems with transmitter diversity in mobile wireless channels[J].IEEE Journal on Selected Areas in Communications,1999,17(3):461-471.
[2]Xie Y Z,Georghiades C N.Two EM-type channel estimation algorithm for OFDM with transmitter diversity[J].IEEE Transactions on Wireless Communications,2003,51(1):106-115.
[3]Zhang J K,Hanzo L,Mu X M.Joint decision-directed channel and noise-variance estimation for MIMO OFDM/SDMA systems based on expectation-conditional maximization[J].IEEE Transactions on Vehicular Technology,2011,60(5):2139-2151.
[4]Liavas A P,Regalia P A,Delmas J P.On the robustness of the linear prediction method for blind channel identification with respect to effective channel undermodeling/overmodeling[J].IEEE Transactions on Signal Processing,2000,48(5):1477-1481.
[5]Wang Z,Mathew G,Xin Y,et al.A robust maximum likelihood channel estimator for OFDM systems[C]//Proceedings of 2007 Wireless Communications and Networking Conference.Hongkong:IEEE,2007:169-174.
[6]Jia M,Wang Z Y,Gu X M.Joint time domain channel and channel length estimation for OFDM system[C]//Proceedings of 2007 International Conference on Communications,Computers and Signal Processing.Victoria,Canada:IEEE,2007:605-608.
[7]Hirotugu A.A new look at the statistical model identification[J].IEEE Transactions on Automatic Control,1974,19(6):716-723.
[8]Larrsson E G,Liu G Q,Li J,et al.Joint symbol timing and channel estimation for OFDM based WLANs[J].IEEE Communications Letters,2001,5(8):325-327.
[9]Tomasoni A,Gatti D,Bellini S,et al.Efficient OFDM channel estimation via an information criterion[J].IEEE Transactions on Wireless Communications,2013,12(3):1352-1362.
[10]Zhang J K,Chen S,Mu X M,et al.Turbo multi-user detection for OFDM/SDMA systems relying on differential evolution aided iterative channel estimation[J].IEEE Transactions on Wireless Communications,2012,60(6):1621-1633.
