STAR模型下退势单位根检验统计量的比较

欧阳敏华

（华南师范大学 经济与管理学院，广州 510006）

0 引言

STAR模型因其能够较好地拟合和预测时间序列动态中的机制转换非线性特征，而被广泛应用于诸如经济周期、购买力平价等经济理论的实证研究中。早期的STAR模型的建模一般都假定时间序列是平稳的，或根据DF等传统单位根检验方法对时间序列数据的平稳性进行检验。然而，越来越多的研究表明传统的DF等单位根检验统计量在非线性模型下的检验势下降得比较厉害，这激发了大量的在非线性模型框架下的单位根检验方法的研究。Kapetantios等（2003）[6]首次在STAR模型框架下建立的单位根检验统计量（以下简称KSS统计量）显著地提高了检验势，有效地拓展了传统的DF单位根检验方法，在时间序列的单位根检验实践中得到广泛应用。

考虑到实际宏观经济时间序列中常常包含确定性趋势成分，Kapetanios和Shin（2008）[4]将Elliot等（1996）[5]在线性模型中的GLS退势方法拓展到了STAR模型下，建立了KSS统计量的GLS退势版本，Monte Carlo模拟研究的结果表明，GLS退势的KSS统计量比OLS退势KSS统计量有更高的检验势。在线性模型框架下，除OLS和GLS退势之外，递归退势也是常用的退势方式之一。张晓峒和白仲林（2005）[6]在对线性模型下退势单位根检验的小样本性质的比较研究中，通过Monte Carlo模拟研究发现递归退势与一些单位根检验方法相结合的方式有更为理想的小样本性质。STAR模型框架下递归退势单位根检验统计量的检验势如何，是否有高于GLS和OLS退势单位根检验的有限样本表现，这一问题目前尚无文献涉及，还有待于进一步的研究。为此，本文尝试将递归退势的方法拓展到STAR模型框架下的单位根检验中，比较研究不同退势方式下单位根检验统计量的有限样本表现，特别是考虑了初始条件对不同退势单位根检验统计量检验势的影响。

1 STAR模型下的退势单位根检验

考虑如下包含确定性线性趋势成分的STAR模型：

其中，εt～iid（0，σ2）。 a 为常数项，b 为时间趋势项的系数，a+bt表示确定性线性趋势成分。F（θ，c;yt-d）为平滑转换函数，θ为平滑参数，c为门限参数，d为时滞参数。遵循Kapetantios等（2003）[3]中平滑转换函数的设定方式，取当 θ→0 时，F（θ，c;yt-d）→0 时，式（1）退化为一个包含确定性线性趋势成分的单位根过程：Δyt=a+bt+εt。显然，当-2＜ϕ＜0，且G（θ，c;yt-k）≠0时，式（1）为一个局部存在单位根但整体平稳的平滑函数为指数函数的STAR过程（ESTAR过程）。这一过程蕴含着，当 yt-1在均衡点附近时，可以是随机游动的，而一旦yt-1远离均衡点时，将存在内生机制使得其向均衡点回复，回复速度取决于平滑参数以及偏离均衡点的距离。

判断时间序列yt是一个单位根过程还是一个全局平稳的ESTAR过程，可建立检验原假设H0∶θ=0，备择假设为H1∶θ＞0。由于在原假设下时间序列yt为一个单位根过程，式（1）中的参数ϕ不可识别，面临假设检验中著名的Davies问题，不可直接在原假设下建立检验统计量进行统计检验。为此，Kapetantios等（2003）[3]建议在θ=0处，将平滑转换函数F（θ，c;yt-d）一阶Taylor展开为多项式函数，建立如式（2）所示的辅助回归模型：

其中，εt为随机误差项。由式（2），三次项作为指数平滑函数的近似。在辅助回归模型中，对时间序列yt是否为单位根过程的统计检验比较容易实施，可类似线性模型下的DF单位根检验，直接建立一个t统计量便可对原假设 H0∶δ=0和备择假设 H1∶δ＜0进行统计检验。

由于式（2）中包含确定性线性趋势成分，为提高单位根检验的检验势，在单位根检验实践中一般应先将确定性线性趋势成分剔除掉，然后再对残差序列进行单位根检验。这种对含有确定性线性趋势成分时间序列的单位根检验的策略，称为退势单位根检验。针对式（2）的退势单位根检验策略为：先将时间序列 yt对（1，t）进行回归得到参数 a，b 的估计值退势后的序列然后再对进行单位根检验，检验模型为：

根据式（3），建立对原假设 H0∶δ=0 和备择假设H1∶δ＜0进行统计检验的t统计量为：

在对时间序列yt退势时，不同退势方式之间的主要差异在于对确定性趋势项中参数估计方法的不同。OLS或GLS退势方式为将时间序列yt对线性趋势项进行OLS或GLS回归，得到a，b的OLS或GLS估计值，进而可以得到退势序列Kapetantios等（2003）[3]、Kapetanios和Shin（2008）[4]探讨了STAR模型下的OLS和GLS退势单位根检验方法。本文将探讨Chang（2002）[1]和Taylor（2002）[2]提出的递归退势方法在STAR模型下单位根检验中的应用，并将其与OLS和GLS退势单位根检验统计量在有限样本表现方面进行比较。Chang（2002）[1]递归退势方式可由式（5）和式（6）表示为：

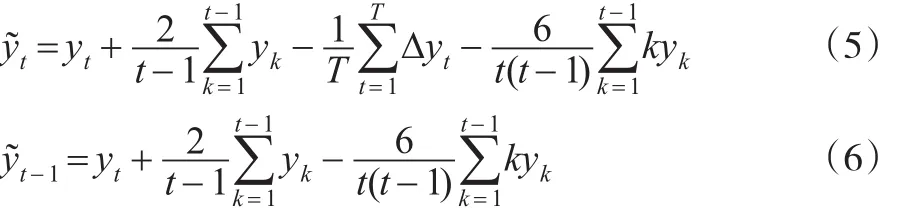
Taylor（2002）[2]的递归退势方式可由式（7）和式（8）表示为：

由式（6）和式（8），Chang（2002）和 Taylor（2002）在对yt-1的退势方式上，两者是相同的；而在对 yt退势上，Chang（2002）考虑了 Δyt项。OLS和GLS退势在对参数a，b的估计上采用的是全样本数据，即采用的是所有样本数据，而递归退势方式在对序列yt退势时，只采用截至时间t的样本数据，然后采用递归的方式逐次估计参数a，b，进而得到时间t的退势序列。时间序列 yt按式（5）和式（6）或式（7）和式（8）退势后的序列代入式（3）中，便可以按式（4）计算递归退势单位根检验统计量的值。本文采用Monte Carlo数值模拟的方式可以得到在STAR模型下采用Chang （2002）和Taylor（2002）递归退势方法的KSS单位根检验统计量的渐近临界值表，结果列于表1。在表1中，列出了显著性水平分别为1%、5%和10%，样本量分别为100、200、500和1000的临界值；各种情形下Monte Carlo模拟次数均为50000次。

表1 采用Chang（2002）和Taylor（2002）递归退势KSS统计量的临界值

2 各种退势KSS统计量的有限样本表现

为比较各种退势方式下KSS单位根检验统计量的有限样本表现，建立如下数据生成过程（DGP）：

其中 εt～N（0，1）。考虑初始条件对检验水平（size）和检验势（power）的影响，设定初始值 y0=ζσ0，其中 ζ={0，±1，±2，±3，±4，±5，±6}，σ0为时间序列 yt的样本标准差，可采用Monte Carlo模拟yt序列的方式计算得到，具体模拟过程可概括为：根据yt的数据生成过程，Monte Carlo模拟初始值为零，样本量为T的序列yt10000次，然后计算样本标准差的平均值。

由式（9）表示的数据生成过程，在考查各种退势方式下KSS单位根检验统计量的检验水平时，设定平滑参数γ=0 ；考查检验势时，设定 γ={0.01，0.05}，ρ={-0.1，-0.5，-1}。参数 ρ，γ取值的不同组合下，按上述DGP设定的模型的特征比较丰富；有些模型比较接近单位根过程，有些模型中平滑转换的非线性特征更为突出，因此，数据生成过程的设定方式可以很好地满足对各退势KSS单位根检验统计量有限样本表现进行全面比较分析的需要。在对各退势KSS单位根检验统计量有限样本表现的Monte Carlo模拟分析时，名义显著性水平设定为0.05，样本量T=100，200，300，模拟次数为10000次。

首先，考查不考虑初始条件影响情形下，即ζ=0，各退势KSS单位根检验统计量有限样本表现，相关结果列于下页表 2。表 2 中，“递归退势I”为Chang （2002）递归退势方式，“递归退势II”为Taylor（2002）递归退势方式。由表2，各退势KSS单位根检验统计量的检验水平都不存在扭曲，实际显著性水平与设定的名义显著性0.05非常接近。设定模型中平滑转换的非线性特征越突出（γ或ρ越大），各退势KSS单位根检验统计量的检验势越高。随着样本量的增大，各退势KSS单位根检验统计量的检验势会显著提高。采用GLS和递归退势方式的KSS单位根检验统计量的检验势要显著高于OLS退势的KSS单位根检验统计量，并且，Taylor（2002）递归退势方式下KSS单位根检验统计量的检验势要好于Chang（2002）递归退势方式。例如，样本量T=200，γ=0.01，ρ=-0.1情形下，Taylor（2002）递归退势方式下KSS单位根检验统计量的检验势为0.220，Chang （2002）递归退势下为0.116，GLS退势为0.125，都要高于OLS退势的0.098。

表2 不考虑初始条件影响，各退势KSS单位根检验统计量有限样本表现 （α=0.05）

考虑初始条件的影响，即ζ≠0，根据式（9）所表示的数据生成过程，采用Monte Carlo数值模拟研究的方式考查各退势KSS单位根检验统计量有限样本表现。在数据生成过程中设定 γ={0.01，0.05}，ρ={-0.1，-0.5，-1}，相应组合下的平滑转换模型共有6种，由于各种模型下各退势KSS单位根检验统计量有限表现的结果是一致的，因此，在表3中只列出了 γ=0.01，ρ={-0.1，-0.5，-1}组合情形下的有关结果。初始条件为负值（ζ＜0）情形下的各种退势KSS单位根检验统计量检验势的特征与初始条件为正值（ζ＞0）情形是一致的，因此，在表3中只列出了初始条件为正情形下的结果。由表3,Taylor（2002）和Chang（2002）递归退势方式下的KSS单位根检验统计量的检验势不受初始条件的影响，而GLS和OLS退势方式下的KSS单位根检验统计量的检验势却受初始条件的影响。GLS退势下的检验势随初始条件的增大下降得比较厉害，并且，增大样本量并不能改善这种影响。这一结果与通常不考虑初始条件下GLS退势单位根检验统计量具有很好的检验势的结论并不一致。图1更直观地展示了各种退势方式下KSS单位根检验统计量检验势的变化特征。Taylor（2002）和Chang （2002）递归退势方式下KSS单位根统计量的检验势比较稳定，且前者的检验势要明显高于后者。OLS退势方式的KSS单位根检验统计量的检验势随初始条件的增大而迅速上升，而GLS退势方式却恰恰相反。

表3 考虑初始条件影响，各退势KSS单位根检验统计量有限样本表现 （γ=0.05，α=0.05）

图1 不同退势方式下KSS单位根检验统计量的检验势

3 结论

本文将Taylor（2002）和Chang （2002）提出的递归退势方式应用到KSS单位根检验统计量的退势单位根检验中，并将其与OLS和GLS退势KSS单位根检验统计量的有限样本表现进行了细致的比较。无论是否考虑初始条件的影响，Taylor（2002）和Chang （2002）递归退势方式的KSS单位根检验统计量都有较好的有限样本表现。不考虑初始条件的影响，GLS退势KSS单位根检验统计量的检验势要显著高于OLS退势；而考虑初始条件的影响，结论却恰恰相反。由于在对时间序列进行退势单位根检验实践中，对于初始条件的大小通常是未知的，因此，采用递归退势的方式可以在一定程度上避免检验势由于初始条件的存在而下降的影响。

[1]Chang,Y.Nonlinear IV Unit Root Tests in Panels With Cross-section⁃al Dependency,Journal of Econometrics,2002,（110）.

[2]Taylor R.Regression-based Unit Root Tests With Recursive Mean Ad⁃justment for Seasonal and Nonseasonal Time Series[J].Journal of Business and Economic Statistics,2002,（20）.

[3]Kapetanios G,Shin Y,Snell A.Testing for a Unit Root in the Nonlin⁃ear STAR Framework[J].Journal of Econometrics,2003,（112）.

[4]Kapetanios G,Shin Y.GLS Detrend-based Unit Root Tests in Nonlin⁃ear STAR and SETAR Models[J],Economics Letters,2008,（100）.

[5]Elliott G,Rothenberg T J,Stock J H.Efficient Tests for an Autoregres⁃sive Unit Root[J].Econometrica,1996,（64）.

[6]张晓峒,白仲林.退势单位根检验小样本性质的比较[J].数量经济技术经济研究,2005,（5）.