两类计数 若干变形

◎戴子钧

(江苏省海门中学高二(5)班，江苏 海门 226100)

在江苏高考中，对排列数与组合数的考查仅在附加题部分出现，这就让众多的文科考生失去了体会排列数与组合数变形的机会，未免有些遗憾.即便对于理科班，因为本章内容的特殊性，所以教师们往往采取点到为止的教学，对题目的分析浅尝辄止.但事实上，排列组合的不易得分和会而不对常常造成我们惨痛的失分，鉴于此，笔者结合平日练习中遇到的一些问题，通过一些“粗加工”与读者共享，以期能有所启发.

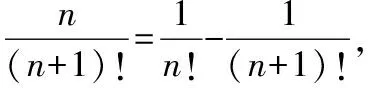
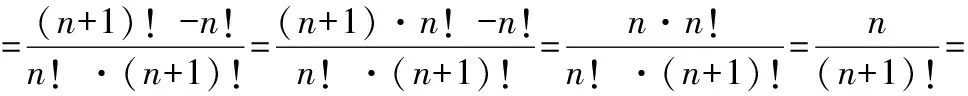
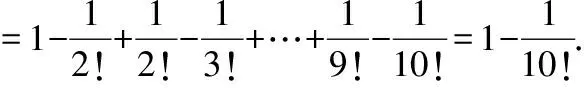
例2(苏教版选修2-3，P18)求证：(n+1)!-n!=n·n!，并化简1·1!+2·2!+3·3!+…+10·10!.

证明左=(n+1)·n!-n!=(n+1-1)·n!=n·n!=右.命题得证.

解原式=2!-1!+3!-2!+…+11!-10!=11!-1!=11!-1.

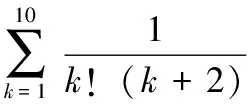
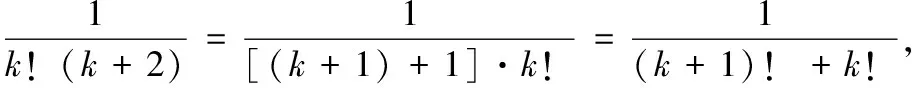
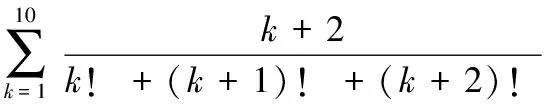
还有一些题目，本身有着特殊的形式，形似神不似，在求解时一定要仔细观察，以免走弯路，请看下题.

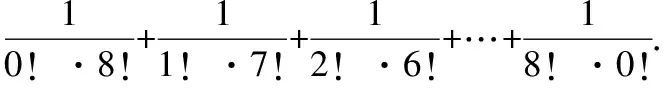
分析分母上a!与b!中a与b的差值不是常数，裂项可能有难度，由于其中a与b之和为定值，可以考虑通过组合数公式的定义求解.

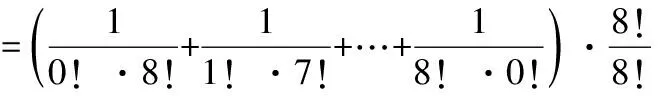
例5求下列各式的值.

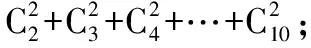
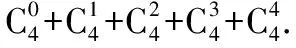
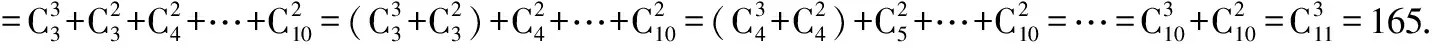
(2)原式=(1+1)4=24=16.

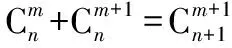
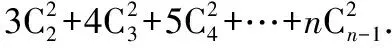
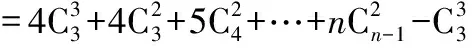
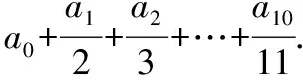
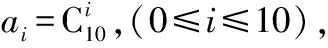
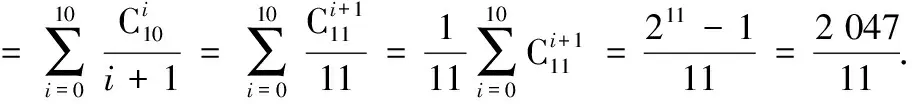
公式的导入使得题目一下子变得简单，比起有的同学可能逐个将a0，a1，a2，…解出，节省了很多的时间.在平时的研究中，笔者又发现等差数列与等比数列的通项an与前n项的和sn经常隐藏在与组合数有关的求和题型中.我们不妨进一步揭开它神秘的面纱.

等差数列{an}中，设首项为a1，公差为d，前n项和为sn.

=(a1-d)(2n-1)+nd·2n-1，

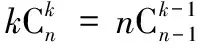
等比数列{an}中，设首项为a1，公比为q(q≠1)，前n项和为sn.