积分求解与几何之间的关系

◎赵一珺

(长沙市长郡中学，湖南 长沙 410002)

积分思想出现在求面积、体积等问题中，在古中国、古希腊、古巴比伦、古埃及的早期数学文献中都涉及了这类问题的思想和方法.如，古希腊的阿基米德(公元前287—前212年)用边数越来越多的正多边形去逼近圆的面积，称为“穷竭法”.中国魏晋时代的刘徽在其《九章算术注》(公元263年)中，对于计算圆面积提出了著名的“割圆术”，他解释说：“割之弥细，所失弥少.割之又割，以至于不可割，则与圆周合体，而无所失矣.”这些都是原始的积分思想.

积分是微积分学与数学分析里的一个核心概念.通常分为定积分和不定积分两种.直观地说，对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值).

一、定积分与面积

可以抽象出积分的原型为求解曲边梯形的面积.

曲边梯形由连续曲线y=f(x)(f(x)≥0)，x轴与两条直线x=a，x=b所围成.

曲边梯形的面积的解决思路：利用元素法的思想求解曲边梯形的面积时，可概括为“分割—取近似—求和—取极限”的步骤.

第一步：分割.将曲边梯形的底，即[a，b]进行分割(用垂直于x轴的直线)，记Δxi=xi-xi-1.

第二步：取近似.取出典型小区域，用矩形面积近似曲边梯形面积ΔSi=f(ξi)Δxi.

第三步：求和.将每个小曲边梯形的面积都用矩形近似，并将所有的小矩形面积加起来.

第四步：取极限.当对曲边梯形底的分割越来越细时，矩形面积之和越近似于曲边梯形面积.

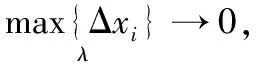
曲边梯形面积的近似值为

当分割无限增加，即小区间的最大长度λ=max{Δx1，Δx2，…，Δxn}趋近于零(λ→0)时，曲边梯形的面积为

二、积分几何意义的运用

由积分的计算过程可以得知，积分的几何意义是介于x轴、函数f(x)的图形及两条直线x=a，x=b之间的各部分面积代数和，在x轴上方的面积取正号，在x轴下方的面积取负号.

下面利用定积分的几何意义来求解问题.

解由定积分的几何意义得：求函数积分即为求该函数在[0，1]上f(x)与x轴所围成的面积，如图所示.求解面积即可.

在不等式的证明中，可以根据不等式中函数的特点，结合积分的几何意义，解决证明问题.

[1]张顺燕.数学的思想、方法和应用[M].北京：北京大学出版社，2002：332.

[2]王志超.高等数学轻松学[M].北京：北京航空航天大学出版社，2015：109.

[3]郭镜明，韩云瑞，章栋恩，等.美国微积分教材精粹选编[M].北京：高等教育出版社，2012：123-126.

[4]王建娥.定积分的几何意义在中学数学中的应用[J].福建中学数学，2010(12)：14-15.

[5]吴赣昌.高等数学[M].北京：中国人民大学出版社，2009：152-153.

[6]刘兴薇.关于定积分概念和性质的应用研究[J].科技资讯，2013(25)：208-210

[7]郑玉军.定积分中两个公式的推广与应用[J].湖南科技学院学报，2015(5)：25-27.

[8]罗威.定积分计算中的若干技巧[J].沈阳师范大学学报：自然科学版，2010(2)：165-168.