借几何画板 破几何难点

◎邬旭亮

(宁波市奉化区新城实验小学，浙江 宁波 315000)

数学是一门研究空间形式和数量关系的科学.它具有高度抽象、逻辑严密、广泛应用的特点.因其本身的学科特性造成了我们学生对有些知识板块的学习困难.这个困难在需要空间想象能力的几何板块就尤为突出.以前我们教师多数都是借助实物或者手工作画来帮助我们的学生进行理解，但是随着信息技术的快速发展，我们的教师更多将信息技术融合与我们的数学教学中，将各种图文融为一体，使大量的几何图形生动地呈现在我们学生的面前，在激发他们的学习兴趣，发展了他们的数学能力，从而获得了最好的教学效果.笔者最近使用的几何画板就在几何板块发挥了很大的作用.

一、几何画板简介

几何画板(原名：The Geometer’s Sketchpad)是由美国Key Curriculum Press公司研制并出版的几何软件.它是一个适用于数学教学的软件平台，为教师和学生提供了一个探索几何图形内在关系的环境.它以点、线、圆为基本元素，通过对这些基本元素的变换、构造、测算、计算、动画和跟踪轨迹等方式，能显示或构造出较为复杂的图形.

二、几何画板在几何板块应用案例

(一)实时呈现，降低难度

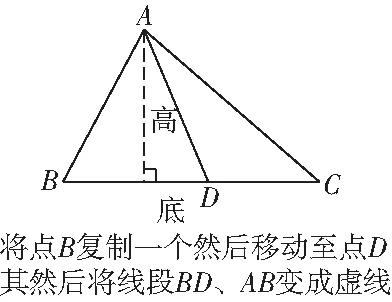
对于人教版四年级下册“三角形作高”想必教过的教师都知道难点在于钝角三角形短边的那条高怎么作.虽然课时目标中并没有要求，但在后续的知识中要用到这个知识点，所以在这个课时我们必须解决这个难点.多数教师在教学时都是自己在黑板上进行完整演示后再让学生尝试，可是我们的学生还是很会出错.这是什么原因呢？笔者觉得有以下几个原因：一是学生对于三角形高的理解不到位.其实这也不能怪学生，因为通过书中的描述学生很自然地将高等同于直角符号.让他们即兼顾直角又要过顶点对于有些学生确实难度大.二是教师在演示过程中由于自身和一些非自身的原因造成的演示不清.笔者对这个教学内容是这样借助信息技术处理的.首先，笔者借用几何画板这个软件画了一个锐角三角形，并分别作出三条高帮助学生复习回顾作高的具体环节.然后在这个三角形的基础上利用动态演示将其中一条三角形的底慢慢缩短，直至将这个三角形变成了一个钝角三角形，而这条底的高则原封不动.然后在原来的三角形的边以虚线的形式呈现(如图所示).学生在看了这个过程之后就会明白这条短边的高其实就是以前锐角三角形的高，不会画的时候只要将这个三角形还原成一个锐角三角形就可以了.这样就通过软件实时动态演示降低了学习难度，学生学习的效果出奇的好.

(二)动态旋转，深入人心

在学习完“平行四边形的面积和周长”以后，我们的学生往往会碰到这样的一个题目：“将长方形拉成一个平行四边形，什么变了？变大还是变小？什么不变？”这个题目学生在理解上存在着一定的困难，所以答案也千奇百怪.我们的教师往往会在黑板上画一个长方形和一个平行四边形将进行比较然后得出结果.但实话说这样单一的对比并不明显，所以学生更多的是靠记忆去保证这个题目的正确率.而笔者则借用几何画板这个软件帮学生解决这个问题.首先笔者在软件中画一个长方形，然后对两个同一条场上的点进行一个程序设置，使得这个长方形绕着没有设置过的两个长的端点旋转，在旋转的过程中将面积的颜色设置成蓝色，边框设置成红色(如右图所示).这样通过动态旋转，学生就看出面积变小了，周长不变.本来教师唠叨十多遍学生也未必记得住，现在即使教师不说，这个知识点也已深入学生的心灵.

(三)无限分割，一目了然

历.于是笔者又想到了几何画板这个软件.首先笔者画了一个圆，然后通过参数设置将圆平均分成四份，取其中的三分涂上颜色.然后通过分子分母不断地增加相同的分数即将圆进行无限分割(分子永远比分母少一份)，学生会发现这样的情况下，分母越大就越接近“1”(如下图所示).通过这样的无限分割，学生对于这个知识点也悄然掌握，同时也让学生感受到了极限的函数思想真是一举两得啊.

《基础教育课程改革纲要(试行)》指出：“大力推进多媒体信息技术在教学过程中的普遍应用，促进信息技术与学科课程的整合，逐步实现教学内容的呈现方式、学生的学习方式、教师的教学方式和师生互动方式的变革，充分发挥信息技术的优势，为学生的学习和发展提供丰富多彩的教育环境和有力的学习工具.”通过以上的案例，我们发现信息技术对需要较好空间想象能力的数学是非常有用的，它能将我们学生不能想象出来的图形一一呈现在我们的眼前，是我们学生非常好的一个学习助手.所以我们要充分地将信息技术整合到数学学科，帮助我们的学生一起揭开数学的本质，使他们爱上数学，快乐的学习数学.

[1]《几何画板》教程——从入门到精通[OL].http：//wenku.baidu.com/view/6003f68984868762caaed579.html

[2]教育部.基础教育课程改革纲要(试行)[Z].2001.

[3]张志敏.《几何画板》在中学数学教学中的应用及其作用[J].新教育时代电子杂志：教师版，2016(34)：153.

[4]刘强.信息技术与高中数学课程整合的理论及实践[D].济南：山东师范大学，2005.