一道奥林匹克问题的推广及拓展
2018-03-23孙丕训张留杰
孙丕训 张留杰
北京市陈经纶中学 (100020)
笔者在阅读文[1]时,发现此问题内涵丰富、规律性较强,于是对此问题进行了更加深入的思考,与大家共勉.


一、问题的推广
我们先从特殊的正多边形入手思考,不难得出:


即便结合正五边形时的结论,也不易猜想出一般规律,于是我们类比文[1]中的证明方法,先探究正n边形时的结论.

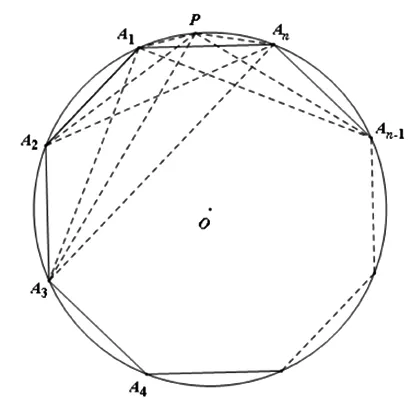
图1
=an-1(ai>0,i=1,2,…,n-1),PA1=x1,PA2=x2,…,PAn=xn(xi>0,i=1,2,…,n).
分别在四边形PA1A2An、PA1A3An、…、PA1An-1An中,运用托勒密定理,可得
A1An·PA2=PA1·A2An+A1A2·PAn、A1An·PA3=PA1·A3An+A1A3·PAn、…、A1An·PAn-1=PA1·An-1An+A1An-1·PAn,注意到正n边形中A1An=A1A2=a1,A2An=A1A3=a2,…,等相等关系,所以有a1x2=a2x1+a1xn、a1x3=a3x1+a2xn、…、a1xn-1=an-1x1+an-2xn,将这n-2个式子相加,得a1(x2+x3+…+xn-1)=(a2+a3+…+an-1)x1+(a1+a2+…+an-2)xn,

下面求这个定值.
设正多边形A1A2…An的外接圆O的半径为R,

图2




二、问题的拓展
我们知道,点是圆的极限图形,将点“膨胀”为圆,或将圆“收缩”为点,可以命制具有新意的问题,文[2]将圆内接四边形的顶点“膨胀”为圆,对托勒密定理进行了如下拓展:
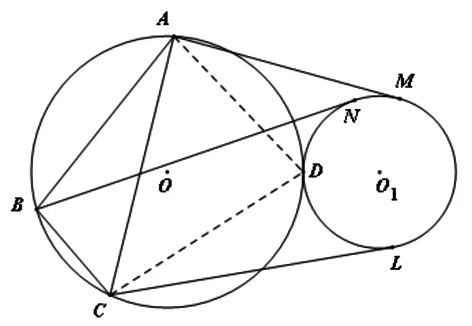
图3
托勒密定理的推广:如图3,已知点A、B、C、D在⊙O上,⊙O1外切⊙O于点D,AM、BN、CL分别切⊙O1于点M、N、L.则AB·CL+BC·AM=AC·BN.
根据文[2]中的推广,我们也可以将结论1进行类似拓展,于是有

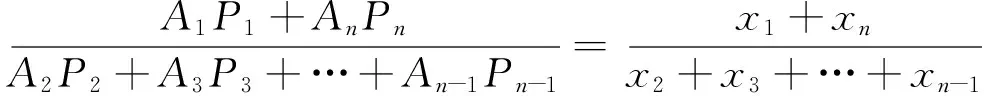
[1]黄金福.数学奥林匹克问题.高536[J].中等数学.2017.8.
[2]张留杰,邱继勇.第1578问题的简证、推广及应用[J].数学通报.2006.7.60-61.
