“圆”形毕露——例谈轨迹思想在解题中的应用

张文海

江苏省苏州实验中学 (215100)

最值问题一直是高中数学教学中的重点内容，同时也是各地高考的热点问题，在高考中占有举足轻重的地位.它具有多元化、广泛性、渗透性的特点，可以说分布在高中数学各个知识点与知识层面中.解答最值问题时,要求学生熟练掌握高中各知识模块的基础知识，综合运用各类数学思想与技能，灵活选择合理的角度和方法.本文笔者根据自身教学实践，从轨迹思想的角度分析探讨处理高中数学一类最值问题的处理方法，希望能给读者带来一定的帮助.

分析2:根据向量的代数属性，联想到条件和问题用坐标表征，将向量问题转化为代数问题进行处理．

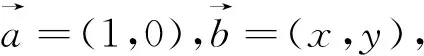
分析1:大多数同学会根据余弦定理及三角形的面积公式，把ΔABC的面积表达为某个自变量的函数，再利用函数的思想求出该函数的最大值．

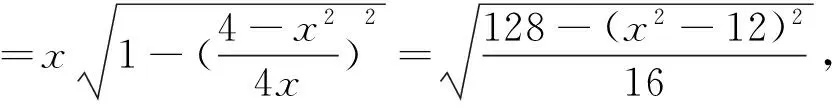
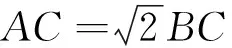
评注：对比两种解法，思路1是研究最值问题的通性通法，思路2把代数问题几何化，利用几何性质，有效地减少了运算量，快速地解决了问题.

分析1:根据向量的代数特征，遇到向量模的问题常通过设出点的坐标来表示模.

分析2:根据向量加法的平行四边形法则，可知四边形PMQN是矩形.

图1

图2

例4 在ΔABC中，点D在边BC上，且DC=2BD，AB∶AD∶AC=3∶k∶1，求实数k的取值范围.

分析1:设BD=x，则DC=2x，因为∠BDA+∠CDA=π，所以

cos∠BDA+cos∠CDA=0，即

图3

分析3:如图3,设AB=3，AC=1,AD=k，以点C为原点，线段AC所在直线为x轴建立直角坐标系xCy，则点A的坐标为(1,0)，因为AB=3，所以点B在以点A为圆心，3为半径的圆上，圆的方程为(x-1)2+y2=9(*).

图4

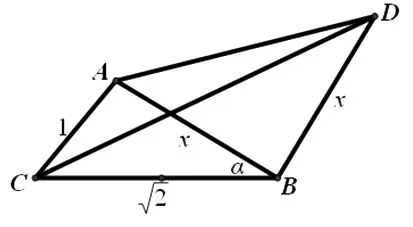
图5

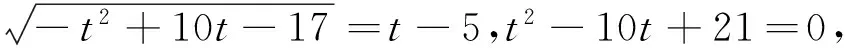
图6

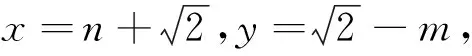
思路决定出路，思维的高度决定解题的长度．纵观近几年高考试卷中的解析几何题目,其涉及面广、综合性强、背景新颖、灵活多样,解题策略较多,渗透着多种数学思想和方法.当动点在一定的条件下运动变化时，研究动点的轨迹是对动点运动结果的一种深刻理解，明确动点的轨迹之后再利用轨迹的几何性质研究最值问题，就有轨可依，有迹可循，往往可以起到另辟蹊径、化繁为简的作用．