斗转星移:坐标平移在圆锥曲线问题中的应用

郝培德 邵建

浙江省杭州学军中学 (310012) 浙江省衢州第二中学 (324000)文

圆锥曲线是高中数学的重要内容，也是高考数学必考的一个知识点.一般地，在处理直线与圆锥曲线的位置关系时，我们通常会联立两者的方程，得到关于某个变量x(或y)的一元二次方程，然后得到一组韦达定理.在大多数情况下这样的计算是相当复杂的，因此学生常常感到难以应对，算不出所以来.近日笔者在高三的复习教学中发现，如果适当地作坐标平移，并巧用“1”的代换，能使一类圆锥曲线题得到简单的解法，可以说是“别有一番滋味”.下面笔者就通过2017年全国卷上的高考题来举例说明，并用此解法作了三个拓广，供参考.

一、考题再现

(1)求C的方程；

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

设直线l对应的直线变为l′，方程为mx′+ny′=1.②

(1)求直线AB的斜率；

(2)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程.

解：(1)易得kAB=1.

在教学过程中，笔者试着对题目的条件进行了变式，但仍用上述的方法，得到了以下三个推广结论.

二、考题拓广

若我们考虑把例1中的条件“直线P2A与直线P2B的斜率的和为-1”改为“直线P2A与直线P2B的斜率之积为-1”，那么直线l是否仍过定点呢？

设直线AB对应的直线变为AB′，方程为mx′+ny′=1.②

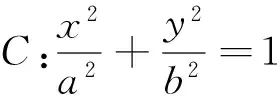
若我们考虑把椭圆换成更一般的圆锥曲线，且动弦PA,PB相互垂直，则直线AB又具有怎样的特点呢？

命题3 已知P(x0,y0)为圆锥曲线Γ上的任一定点，PA,PB为动弦，且PA⊥PB,则直线AB为一簇平行直线或是过定点的直线系.

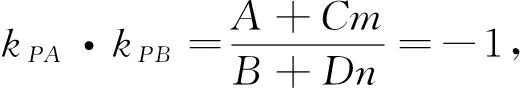
(1)若A+B=0,且C=0,则直线AB的方程为x=0；

(4)若A+B≠0,但C=0,则直线AB的方程为x=0.

[1]傅建红.一类悄然升温的“嵌套函数”零点相关问题例谈[J].中学数学研究(江西),2013(12):10-12.