组合循环生成法在柯克曼三元系中的应用
2022-07-27谢玉枚高海燕
谢玉枚,杨 玮,高海燕
(1.福建江夏学院电子信息科学学院,福建 福州 350108,2.厦门理工学院电气工程与自动化学院,福建 厦门 361024)
1850年,英国教会的教区长柯克曼Kirkman提出:一位女教师每天都带领着她的15位女学生去散步,她要求学生们排成三人一组,一共五组的队列随她前进,问能否给出一个一周内的队列安排,使得每两名学生在七天中都恰有一天排在同一组。
从柯克曼于1850年提出女生散步问题至今,众多学者和爱好者对柯克曼三元系的构造问题进行了许多研究和探讨,它开创了组合设计的先河,其中BIBD表示为B[k,λ;v]是组合设计最重要的一类。它指的是v元集V中一些K-子集(称为区组)的族β使得V的每个2-子集都恰好出现于β的λ个区组中[1]。 当k=3,λ=1时,这种设计被称为斯坦纳(Steiner)三元系,记作STS(v),STS(v)存在的充分必要条件为当且仅当v≡1 or 3(mod 6)[2]。如果β可拆分为若干个子族,使得每个子族都构成集合V的一个分拆,则称其为可分解的斯坦纳三元系,用KTS(v)表示,KTS(v)存在的充分必要条件为当且仅当v≡3(mod 6)。
迄今为止,众多学者对BIBD进行了大量研究,并且提出了构造STS(v)和KTS(v)的递归方法。其中一种经典方法为Chaudhuri和Wilson等[2]、Hanani等[3]提出的基于柯克曼框架来构造柯克曼三元系;另外一种方法是使用分组设计来解决BIBD的构建问题[4-6]。在这些构造方法中,循环BIBD和单旋转BIBD由于它们的代数结构简单且实用性强,许多学者对其进行了大量的研究,其中Phelps等[7]首先介绍了单旋转STS(v)的概念,Jimbo等提出了递归构造方法来构造1-旋转S teiner-2设计和可解析的1-旋转Steiner-2设计[8-10]。这些方法都是使用群论、图论和代数工具来解决BIBD的构造问题。
最近有学者提出了从不同的角度解决STS(v)和KTS(v)的研究。例如,将柯克曼女生散步问题作为社会高尔夫球手问题的特定实例,可以通过约束编程[11]和约束满足问题[12]来解决。Barnier[13]提出了一种检查对称性的算法,并在几秒钟内解决了柯克曼的女学生问题。Lardeux等[14]通过表达模型化集合约束问题并将其自动编码为SAT实例来解决社交高尔夫球手问题。
在本文中,从计算机科学的角度提出了一种递归构造的KTS(v)新方法,通过建立一个用于构造v≡3 mod 12的KTS(v)的模型,这不是文献[13]中提出的集合模型,而是基于罗洪田[15]提出的将集合V的元素对应于圆上的点的模型,将几何图形与区组结合起来,圆上的三角形作为KTS的区组,并提出了一种计算机算法来生成KTS(v)。
求解从n个元素中取m个元素的组合,可以把n个元素均匀分布在圆周上,这样求解Cmn的组合就转换为在等分圆周上求解m边形。圆周上的m边形沿着圆周转动可产生n个m边形。例如,当n=8,将8个数字均匀分布在等分圆周上,求解的组合情况就变换成在圆周上求解3边形,如图1所示,3边形1-2-3沿着圆周转动可产生8个各不相同的3边形,可以通过对3边形1-2-3作数字循环写出其同构3边形,如表1所示。这8个3边形有什么特点呢?它们的相邻元素间距离相等,因此认为它们结构相同。

图1 8等分圆

表1 3边形123的同构3边形
将n个元素均匀分布在圆周上,圆周被分成n个弧段,两个元素所夹的弧的段数称为弧长。两个元素所夹有大小两个弧段,其和为n,现约定以小弧段代表弧长,所以圆周上两个元素的弧长为:当两元素对应的数字之差的绝对值小于等于n/2,弧长等于数字之差;当两元素对应的数字之差的绝对值大于n/2,弧长等于n减去数字之差。
在n等分圆周上,当n等于偶数时,基本的弧长有n/2个,分别为:1,2,3,…,n/2;当n等于奇数时,基本的弧长有(n-1)/2 个,分别为:1,2,3,…,(n-1)/2。
用m边形中的相邻元素间的弧长表示m边形的结构。例如,当n=8,m=3时,3边形123的结构用(1,1,2)表示,其循环产生的8个3边形的结构也是(1,1,2),且这8个3边形各不相同,如表1所示。
在n=8等分圆周上,结构不同的3边形通过计算得到了7个不同结构3边形,如表2所示,这7个3边形循环转动可分别产生8个不同的3边形,于是8等分圆周上3边形的总数为:8×7=56,恰好等于。
表2 的所有组合

表2 的所有组合
编号12345678(1,1,2)123234345456567678781812(1,2,3)235346457568671782813124(1,3,4)125236347458561672783814(1,4,3)126237348451562673784815(1,3,2)127238341452563674785816(2,2,4)246357468571682713824135(2,3,3)136247358461572683714825
从表2可知,当n=8,m=3时,圆周上任意一个结构的3边形沿着圆周转动都能产生8个不相同的3边形,从而的所有组合由不同结构的3边形分别沿着圆周循环转动产生。然而并不是对任意n和m,圆周上的m边形沿着圆周转动都能产生n个不相同的3边形,例如当n=9时,将9个数字均匀分布在等分圆周上,3边形1-4-7沿着圆周转动产生了9个3边形,如表3所示。

表3 3边形147转动产生的3边形
从表3可以看出,3边形1-4-7产生的9个3边形中有3组重复项(表中√所示)。同时注意到求组合时,n与m有公因子3。是否可以作这样的假设,在使用循环法求解时,当n与m没有公因子时,圆周上任意结构的m边形沿着圆周转动生成的n个m边形是不相同的;当n与m有公因子时,圆周上至少有一个m边形沿着圆周转动生成的n个m边形是有重复项的。
2 n与m的公因子
现令M=((n-1)(n-2)…(n-m+1))/m!,所以。
当m与n有公因子r时,r可以同时被n与m整除,这就意味着,在n等分圆周上,m边形中的m个元素可以被分为r块,每一块有m/r个元素,则m边形可表示为(m1,m2,…,mr),其中mi(1≦i≦r)为每块之间的元素;n也可以被分为r组,每组之间的弧长为n/r。当m边形(m1,m2,…,mr),每个块 mi结构相同,相邻mi间的弧长相等为n/r时,m边形沿着圆周移动n/r个单位后,m边形不变,因此m边形沿着圆周转动一圈后会产生r个相同的m边形。
当公因子等于2时,4边形中的4个元素就被分为2块,每块有2个元素,相邻块之间的弧长为:8/2=4,令4边形第一块的第一个元素为1,因为相邻块之间的弧长为4,所以第二块的第一个元素为5,所以这个4边形可以写成1x 5y,其中2≤x≤4,6≤y≤8,且这两块的结构相同,所以还得满足y-5=x-1。于是可以得到满足条件的3个4边形,如表4所示,其中第1个和第3个4边形结构相同,它们都有2组重复项,如表4中√所示。而第2个4边形不仅满足公因子等于2的条件,如表4中√所示,同时还满足公因子等于4的条件。
表4 的组合类型

表4 的组合类型
编号123456781(1,3,1,3)√1256347734784581√56126723783481452(2,2,2,2)√*13572468*35714682√*57136824*724682463(3,1,3,1)√1458256136724783√5814612573478347
当公因子等于4时,4边形中的4个元素就被分为4块,每块有1个元素,相邻块之间的弧长为:8/4=2,令4边形的第一块的元素为1,因为相邻块之间的弧长为2,所以第二块的元素为3,第三块的元素为5,第四块的元素为7,所以这个四边形为1-3-5-7,沿着圆周转动可产生4组重复项,如表4中*所示。
当n与m没有公因子,在n等分圆周上,m边形中的m个元素不能被分为整数块,在转动过程中不会产生重复项,所以产生的n个m边形是各不相同的。
定理1当n与m没有公因子时,将不同结构的m边形作循环可直接生成n×M个m边形,这n×M个m边形就是的所有组合,其中不同结构的m边形的个数为M,其中M=((n-1)(n-2)…(n-m+1))/m!,且当n与m没有公因子时,M一定为整数;
定理2当n与m有公因子r时,至少存在一个m边形作循环时产生r组重复项,的所有组合等于不同结构的m边形作循环同时去掉重复项。
3 m边形相同结构的判定
标记m边形时都是按顺时针方向进行的,m边形中的m个点都可以作为起始点。例如,3边形1-2-3,除了以1为起始点外,还可以以2和3为起始点,3边形1-2-3,2-3-1和3-1-2是完全相等的,如表5所示,这3个3边形和其结构都随着起始点的变化向左循环移动。因此,若一个m边形的结构循环左移k(0≤k<m)个单位后,与另一个m边形的结构相等,我们就判定这两个m边形的结构相等。

表5 3边形123向左循环移动
通过两个例子来说明,在7等分圆周上,有3边形2-3-7(1-3-2)和1-3-4(2-1-3),3边形237向左循环移动2个单位后,其结构与3边形1-3-4(2-1-3)相等,如表6所示,因此这两个3边形的结构相等。

表6 3边形237向左循环移动
同样在7等分圆周上,有3边形6-7-2(123)和3边形1-3-4(213),3边形6-7-2循环左移过程中没有找到与3边形1-3-4(213)重合的结构,如表7所示,因此这两个3边形的结构不同。

表7 3边形672向左循环移动
4 求解不同结构的m边形
m边形在圆周内是封闭的,因此m边形相邻元素之间的弧长之和应该等于n。因为两个元素之间的弧长是用小弧长来表示的,所以圆周上的m边形分为两类,第一类m边形的m个元素只分布在半圆内,这类m边形相邻元素之间的弧长之和不等于n,m个弧长中最大的弧长等于其他m-1个弧长之和且小于n/2;第二类元素分布在整个圆内,m边形的m个弧长之和等于n。例如,在8等分圆周上,3边形1-2-3(112)的三个元素只分布在半圆内,属于第一类3边形;3边形1-3-6(233)分布在整个圆内,属于第二类,3个弧长之和等于8。
计算m边形的结构可以转化为一序列约束条件,令m边形的结构为(x1,x2,…,xm),其中x1,x2,…,xm为m边形的m个弧长。因为m边形的结构循环左移可产生m种等价结构(如表5所示),使得在找出不同结构的m边形时还得排除等价的结构,因此令m边形(x1,x2,…,xm)的标准结构为:最后一个弧长xm最大,也就是x1≤x2≤…≤xm。
因为m<3时,m边形的结构可直接写出,所以以下的论述是针对m≥3的情况。
对于第一类m边形,xm为弧长中最大的,则有下列约束:

对于第二类m边形,其m个元素分布在整个圆上,前m-1个弧长之和大于等于n/2,且m边形的标准结构必须满足x1≤x2≤…≤xm,通过上文论述,m边形的结构(x1,x2,…,xm)循环左移时会产生m种等价结构(如表5所示),例如m边形的结构循环向左移动1个单位,其结构变为(x2,x3,…,xm,x1),若它也满足m边形的标准结构的约束条件则有:x2≤x3≤…≤xm≤x1,于是整体约束需要同时满足 x1≤x2≤…≤xm和 x2≤x3≤…≤xm≤x1,得到 xm=x1。 当 m 边形结构(x1,x2,…,xm)循环左移 k(0<k<m)个单位后,若其结构也满足标准结构则有xm=x1=x2…=xk,在求解m边形结构的过程中,是要排除等价结构的,从而令x1<xm就可以排除等价结构,于是求解第二类m边形时有约束:

m边形的不同结构的数量为S1∪S2,举一个例子来说明。当n=14,求在n=14等分圆上3边形的结构,n=14,则有 1,2,3, …,7 个弧长,3 边形的结构可以表示为(x1,x2,x3),有:

求解S1和S2得到的3边形的不同结构见表8所示,第一类3边形为15个,第二类3边形为 11个,3边形的不同结构一共有26个。

表8 3边形的不同结构
5 m边形的奇偶属性
若m与n没有公因子,m边形沿着圆周转动可以产生n个不同的m边形,这n个m边形根据奇偶属性可分为2类,在同一个类里,所有m边形的奇偶属性相同。
m边形的奇偶属性为m边形中m个数字的奇偶性,例如当n=14,m=3时,3边形123可产生14个3边形,这14个3边形可分为2类,如表9所示,在第一类里所有3边形的奇偶属性为(奇,偶,奇);在第二类里所有3边形的奇偶属性为(偶,奇,偶)。

表9 3边形123的奇偶属性
在n等分圆周上,可以通过上述求解约束方程来求解m边形的不同结构,同时已知m边形的结构也可以求m边形的初始化值,根据奇偶属性,对于每个m边形结构,有两种初始化值。若已知m边形的结构为(x1,x2,x3,…xm),则对应的m边形为y1,y2,y3,…,ym。
第一类初始化值为:yi+1=yi+xi,1≤i<m,y1=1
第二类初始化值为:yi+1)=yi+xi,1≤i<m,y1=2
当n=14时,不同结构的3边形的初始化值如表10~11所示。

表10 n=14时3边形的第一类初始化值

表11 n=14时3边形的第二类初始化值
6 在科克曼三元系中的应用

图2 n=14等分圆
由上文可知,n=14,m=3时,有26个不同结构的3边形,在n=14的等分圆周上圆周3边形的数量为26×14=364,恰好等于。圆心3边形为圆心15与圆周上的2个元素的组合,其3边形结构用(L,R,R)表示,其中L为n=14等分圆周上的2个元素的弧长,R表示半径;当n=14时,如图2所示,其基本弧长有:1,2,3,…,7,其中弧长等于7的2边形只能循环产生7个不同2边形,那么对应的不同圆心3边形也只有7个,如表12所示;其他的弧长对应2边形都可生成14个不同的2边形,其对应的圆心3边形也有14个,所以圆心3边形的总数为:14×6+7=91,恰好等于。 n=14,其圆心3边形的结构和初始化值如表13所示。
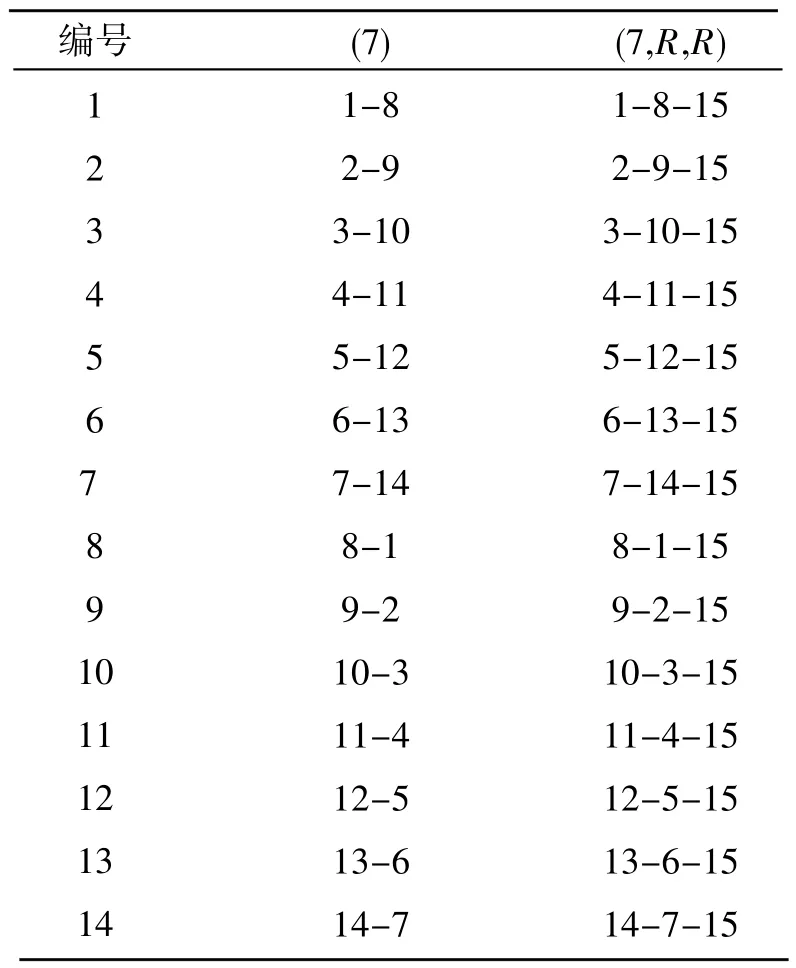
表12 弧长7生成的2边形和圆心3边形

表13 n=14圆心3边形及结构
柯克曼三元系的一个平行类可以表示为圆上的点(包括圆心)组成的3边形,如图3所示,有柯克曼三元系的平行类:1-2-15,4-5-8,7-11-13,10-12-3,6-9-14。这5个3边形,每次循环转动2个单位,可以生成一个有效柯克曼三元系,如表14所示。

图3 柯克曼三元系的平行类
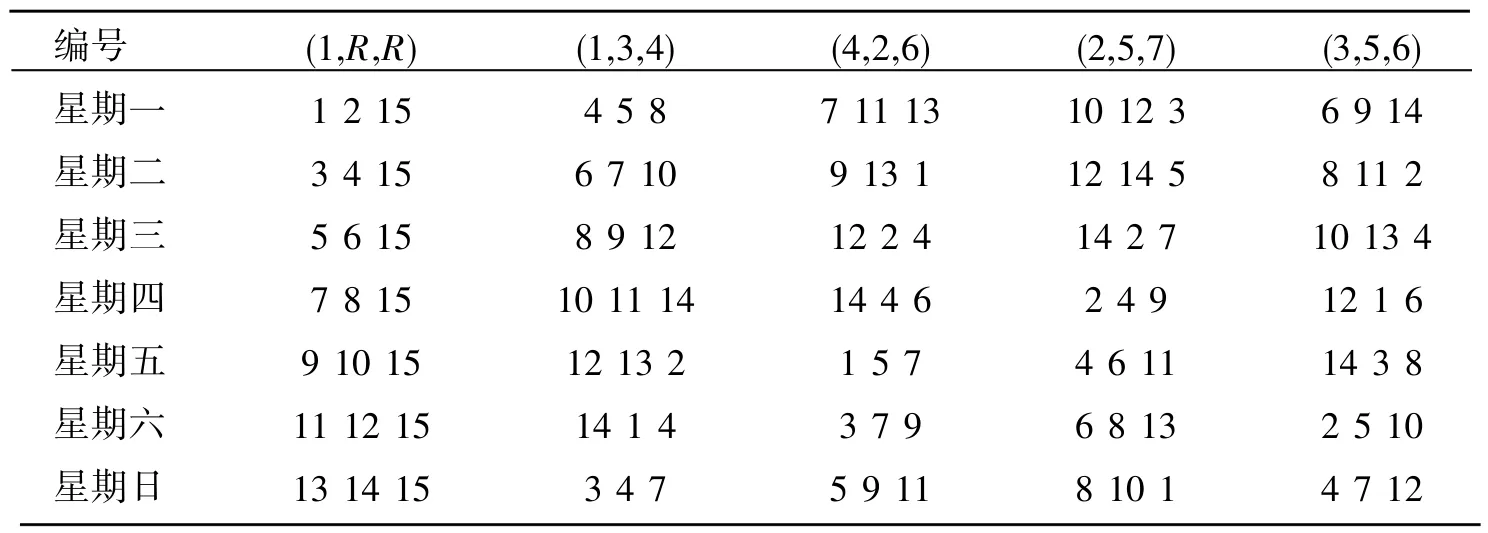
表14 一个柯克曼三元系的构造
从表14可知,每个平行类的5个3边形的结构都是相同的,所以要用组合的循环生成法生成柯克曼三元系的首要任务就是找到有效的3边形结构序列,例如找到一个有效的3边形结构序列:(1,R,R),(1,3,4),(4,2,6),(2,5,7),(3,5,6)。
怎么样的3边形结构序列才是有效的呢?用圆周3边形和圆心3边形构造KTS(15)的一个平行类,KTS(15)中有一个三元系包含数字15,所以KTS(15)的一个平行类包含1个圆心3边形和4个圆周3边形,圆心3边形有一个有效弧长,圆周3边形有3个有效弧长,则一个平行类的总弧长数量为1+3×4=13,那么若要用圆心3边形和圆周3边形表示柯克曼三元系,其弧长应该怎么分配呢?
结论是:弧长1,2,3…6在3边形结构序列中使用两次,且对于每个弧长,两次使用产生的2边形分别属于不同奇偶属性,弧长7使用一次时,可满足生成柯克曼三元系KTS(15)的条件。
原因为,在n=14的等分圆周上一共有7个基本弧长,弧长1,2,3,…,6可循环产生14个不同2边形,因为KTS(15)有7个平行类,所以弧长1,2,3,…,6在3边形结构序列中可以使用两次,又因为在KTS(15)的35个三元系中,任意两个数字只能结合一次,所以对于弧长1,2,3,…,6,每次使用时产生的2边形必须分别为不同奇偶属性,例如对于表14的结构序列,(1,R,R)和(1,3,4)都使用了弧长 1,弧长1 在(1,R,R)和(1,3,4)中对应的2边形如表15所示,分别为不同的奇偶属性。而对于弧长7,只能循环产生7个2边形,所以弧长7只能使用一次。

表15 弧长1在不同结构里对应的2边形
对于n=14,满足柯克曼三元系的结构序列如附件1所示。
1.在附件1中取出一个3边形结构序列,例如第8个:(1,R,R),(1,3,4),(4,2,6),(2,5,7),(3,5,6)
2.对于上述3边形结构序列中的圆心3边形的初始化是固定,根据表13直接初始化;对于圆周3边形,有两种初始化形式,根据柯克曼三元系的约束条件,选择对应的初始化值,使得弧长1,2,3,…,6所对应的两个线段为不同奇偶属性。
例如,对于上述3边形结构序列有:
1)对于弧长1,出现在(1,R,R)和(1,3,4)中,圆心3边形直接初始化,(1,R,R)的3边形初始化为1 2-15,于是弧长1对应的线段为1-2;对(1,3,4)进行初始化时,弧长1对应的线段必须和1-2(1)为不同奇偶属性,所以(1,3,4)的初始化3边形为2-3-6;
2)对于弧长3,出现在(1,3,4)和(3,5,6)中,在(1,3,4)中对应的线段为3-6,对(3,5,6)进行初始化时,弧长3对应的线段必须和36(3)为不同奇偶属性,所以(3,5,6)的初始化3边形为2-5-10;
3)对于弧长4,出现在(1,3,4)和(4,2,6)中,在(1,3,4)中对应的线段为2-6,对(4,2,6)进行初始化时,弧长4对应的线段必须和2-6(4)为不同奇偶属性,所以(4,2,6)的初始化3边形为1-5-7;
4)对于弧长2,出现在(4,2,6)和(2,5,7)中,在(4,2,6)中对应的线段为5-7,对(2,5,7)进行初始化时,弧长2对应的线段必须和5-7(2)为不同奇偶属性,所以(2,5,7)的初始化3边形为2-4-9;
5)对于弧长 5,出现在(3,5,6)和(2,5,7)中,(3,5,6)已初始化为 2-5-10,(2,5,7)已初始化为 2-4-9,弧长 5在(3,5,6)对应的线段为5-10,在(2,5,7)对应的线段为49,弧长5对应的两条线段有不同的奇偶属性。
6)对于弧长 6,出现在(3,5,6)和(4,2,6)中,(3,5,6)已初始化为 2-5-10,(4,2,6)已初始化为 1-5-7,弧长 6在(3,5,6)对应的线段为2-10,在(4,2,6)对应的线段为1-7,弧长6对应的两条线段有不同的奇偶属性。通过上面的分析得到3边形结构序列的初始化值,如表16所示。

表16 3边形结构序列的初始化值
3.要满足柯克曼三元系每个平行类必须包含1到15的数字,令圆心3边形的初始化值1-2-15不变,4个圆周3边形循环加2,得到一个2维数组,如表17所示,然后在数组里搜索满足柯克曼三元系一个平行类(带底纹),最后得到3边形结构序列的初始化值,如表18所示。

表17 圆周3边形生成的2维数组

表18 柯克曼三元系的一个平行类
对表18中的3边形循环转动2个单位生成柯克曼三元系,如表14所示。
7 结论
在本文中,从计算机科学的角度提出了一种递归构造柯克曼三元系的新方法,将集合V中{1,2,3,...,v}中的元素对应在等分圆上,一个柯克曼平行类可以由圆上的区块(三角形)表示。我们给出构造KTS(v)的第一并行类的约束,以及如何构造KTS(v)的第一并行类,通过固定点v并沿着圆周上循环转动2个单位可以得到柯克曼三元系的构造。当v=15时,依照上述组合循环生成法的步骤写程序运行可获得44个解。尽管已经存在构造KTS(v)的传统方法,但是以上提供的方法是可针对v≡3 mod 12递归构造柯克曼三元系,研究结果将为递归构造柯克曼三元系提供新的思路和方法。
